X 12y 210 And X 6y 90 Then X
News Co
Mar 26, 2025 · 4 min read
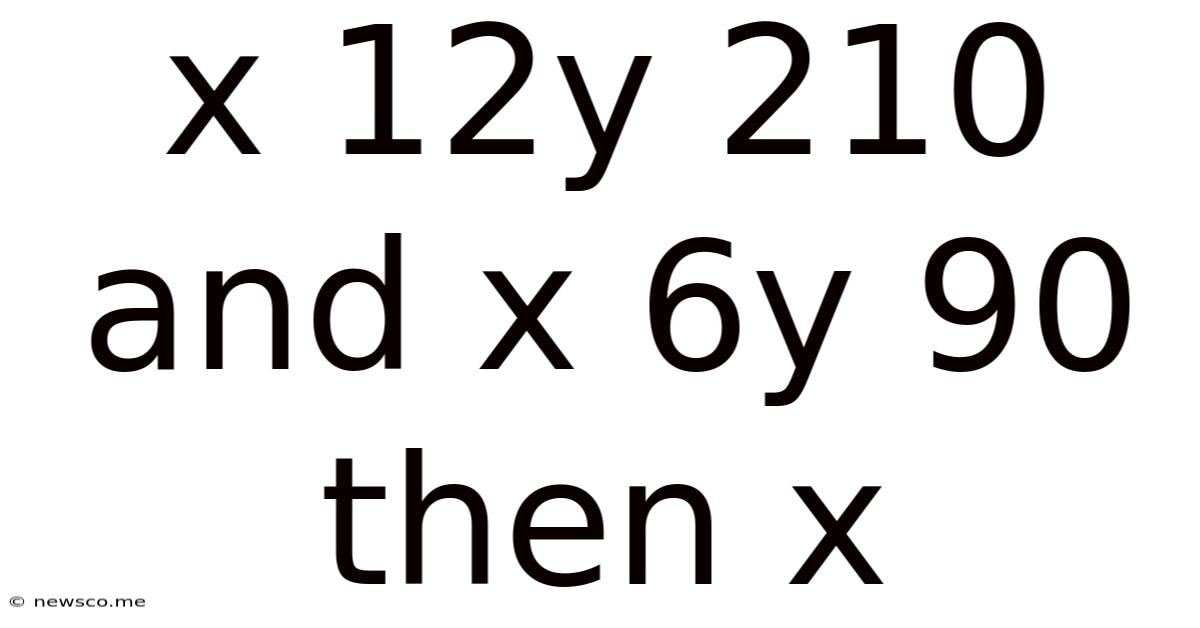
Table of Contents
Solving Simultaneous Equations: A Deep Dive into x + 12y = 210 and x + 6y = 90
This article will provide a comprehensive guide to solving simultaneous equations, specifically focusing on the equations x + 12y = 210 and x + 6y = 90. We'll explore multiple methods for finding the values of x and y, delve into the underlying mathematical principles, and discuss practical applications of simultaneous equations in various fields.
Understanding Simultaneous Equations
Simultaneous equations, also known as systems of equations, involve two or more equations with two or more variables. The goal is to find the values of the variables that satisfy all equations simultaneously. These equations often represent relationships between different quantities in a real-world problem. For instance, they can model the costs and quantities of different products, the speeds and distances of moving objects, or even the interactions within complex systems.
Our focus here is on a specific system:
- x + 12y = 210
- x + 6y = 90
This is a linear system because both equations represent straight lines when graphed. The solution represents the point where these two lines intersect.
Methods for Solving Simultaneous Equations
Several methods can be employed to solve simultaneous equations. We'll explore three common approaches: elimination, substitution, and graphical methods.
1. Elimination Method
The elimination method aims to eliminate one variable by adding or subtracting the equations. In our case:
-
Subtract the second equation from the first: (x + 12y) - (x + 6y) = 210 - 90. This simplifies to 6y = 120.
-
Solve for y: Divide both sides by 6: y = 20.
-
Substitute the value of y back into either equation to solve for x: Let's use the second equation: x + 6(20) = 90. This simplifies to x + 120 = 90.
-
Solve for x: Subtract 120 from both sides: x = -30.
Therefore, the solution to the system of equations is x = -30 and y = 20.
2. Substitution Method
The substitution method involves solving one equation for one variable and substituting that expression into the other equation.
-
Solve one equation for one variable: Let's solve the second equation for x: x = 90 - 6y.
-
Substitute this expression for x into the first equation: (90 - 6y) + 12y = 210.
-
Simplify and solve for y: 90 + 6y = 210; 6y = 120; y = 20.
-
Substitute the value of y back into either equation to solve for x: Using the equation x = 90 - 6y, we get x = 90 - 6(20) = -30.
Again, the solution is x = -30 and y = 20.
3. Graphical Method
The graphical method involves plotting both equations on a graph. The point of intersection represents the solution. While this method is visually intuitive, it can be less accurate than algebraic methods, especially when dealing with non-integer solutions.
To plot the equations:
-
Rewrite each equation in slope-intercept form (y = mx + b):
- x + 12y = 210 => y = (-1/12)x + 17.5
- x + 6y = 90 => y = (-1/6)x + 15
-
Plot the lines: Each equation represents a straight line with a slope (m) and y-intercept (b). Plot these lines on a graph.
-
Find the point of intersection: The coordinates of the point where the lines intersect represent the solution (x, y). You'll find this intersection point at x = -30 and y = 20.
Verifying the Solution
It's crucial to verify the solution by substituting the values of x and y back into both original equations:
- Equation 1: -30 + 12(20) = -30 + 240 = 210. This is correct.
- Equation 2: -30 + 6(20) = -30 + 120 = 90. This is also correct.
Since the values satisfy both equations, we've confirmed our solution.
Real-World Applications of Simultaneous Equations
Simultaneous equations have wide-ranging applications in various fields:
- Economics: Analyzing supply and demand, determining market equilibrium, and modeling economic growth.
- Engineering: Solving circuit problems, calculating forces in structures, and optimizing designs.
- Physics: Determining velocities and accelerations of moving objects, analyzing forces in equilibrium, and modeling projectile motion.
- Chemistry: Calculating concentrations of solutions, determining reaction rates, and balancing chemical equations.
- Computer Science: Solving optimization problems, developing algorithms, and modeling complex systems.
- Business: Calculating profits and losses, managing inventory, and forecasting sales.
Advanced Concepts and Extensions
The techniques discussed here form the foundation for solving more complex simultaneous equations. These extensions include:
- Non-linear systems: Systems involving equations that are not linear (e.g., quadratic, exponential, or trigonometric equations). Solving these often requires more advanced techniques.
- Systems with more than two variables: While the elimination and substitution methods can be extended, matrix methods (like Gaussian elimination or Cramer's rule) become more efficient for larger systems.
- Systems with inequalities: These systems involve inequalities instead of equalities and represent regions on a graph rather than single points.
Conclusion
Solving simultaneous equations is a fundamental skill in mathematics with far-reaching applications across numerous disciplines. Understanding the different methods—elimination, substitution, and graphical—and knowing when to apply each is crucial. By mastering these techniques, you equip yourself with a powerful tool for tackling complex problems and gaining a deeper understanding of relationships between variables in various real-world scenarios. The example of x + 12y = 210 and x + 6y = 90 serves as an excellent entry point into this vital area of mathematics. Remember to always verify your solutions to ensure accuracy and build confidence in your mathematical abilities.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 12y 210 And X 6y 90 Then X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.