X 2 2x 3 X 2
News Co
Apr 22, 2025 · 5 min read
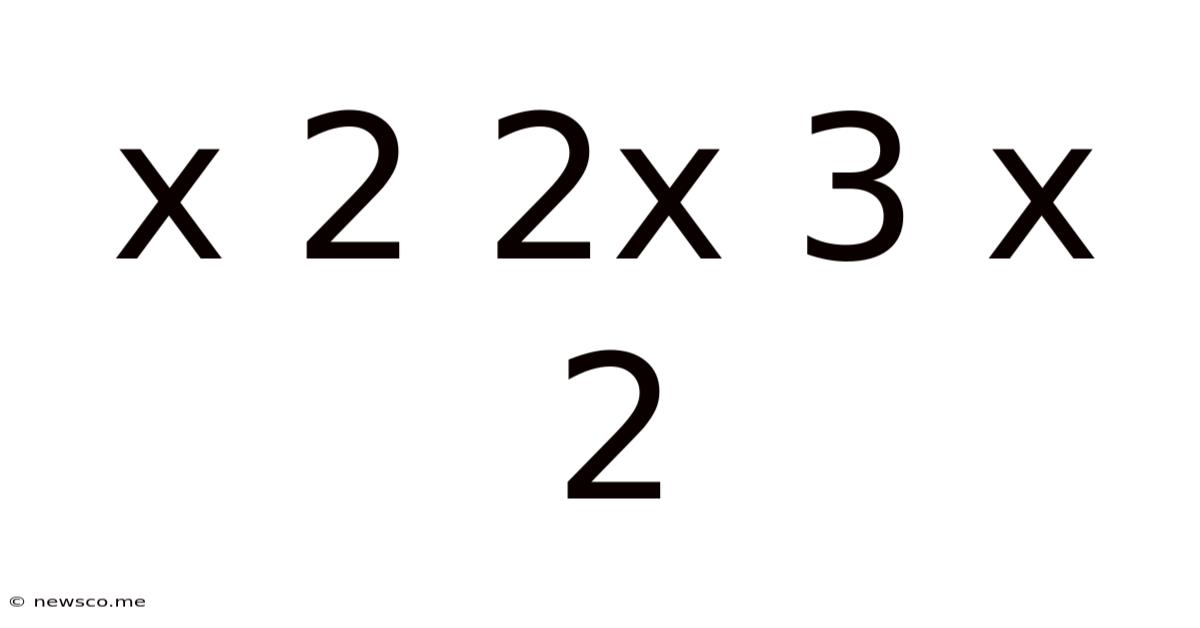
Table of Contents
Decoding the Mystery: A Deep Dive into the Mathematical Expression "x² + 2x + 3x²"
The seemingly simple mathematical expression "x² + 2x + 3x²" might look intimidating at first glance, particularly for those who haven't delved deeply into algebra. However, understanding this expression unlocks a world of possibilities in mathematics, paving the way for more complex equations and concepts. This comprehensive guide will break down this expression step-by-step, exploring its simplification, applications, and connections to broader mathematical principles. We'll cover everything from fundamental algebraic concepts to practical applications, ensuring a thorough understanding for beginners and a refresher for those more experienced.
Understanding the Basics: Variables and Exponents
Before diving into the simplification process, let's refresh our understanding of the fundamental components of this expression: variables and exponents.
Variables: The Unknowns
In mathematics, a variable is a symbol, typically represented by a letter (like 'x' in our expression), that stands for an unknown value. The beauty of variables lies in their flexibility; they can represent any number, allowing us to create general rules and equations applicable across various scenarios. In our expression, 'x' represents a single, unknown value.
Exponents: Repeated Multiplication
The small number written slightly above and to the right of a variable or number is called an exponent. It indicates the number of times the base (the variable or number) is multiplied by itself. For example:
- x² (x squared) means x * x
- x³ (x cubed) means x * x * x
Understanding exponents is crucial for simplifying and manipulating algebraic expressions.
Simplifying the Expression: Combining Like Terms
The core of simplifying "x² + 2x + 3x²" lies in the concept of like terms. Like terms are terms that contain the same variable raised to the same power. In our expression, we have three terms:
- x²
- 2x
- 3x²
Notice that x² and 3x² are like terms because they both have the variable 'x' raised to the power of 2. The term '2x' is a different kind of term because the variable 'x' is raised to the power of 1 (which is usually not explicitly written).
To simplify, we combine the like terms by adding their coefficients (the numbers in front of the variables):
1x² + 3x² = 4x²
Therefore, the simplified expression becomes:
4x² + 2x
This simplified form is equivalent to the original expression but is much easier to work with and understand.
Expanding on the Concepts: Further Algebraic Manipulations
The simplified expression, 4x² + 2x, opens doors to a variety of algebraic manipulations. We can explore several key areas:
Factoring: Finding Common Factors
Factoring involves breaking down an expression into smaller parts (factors) that, when multiplied together, produce the original expression. In the case of 4x² + 2x, we can find a common factor of 2x:
2x(2x + 1)
This factored form is particularly useful when solving equations or simplifying more complex expressions.
Expanding: Distributing Terms
The opposite of factoring is expanding, where we distribute a term across parentheses. For example, if we start with the factored form 2x(2x + 1), expanding it would give us:
2x * 2x + 2x * 1 = 4x² + 2x – our original simplified expression.
Solving Quadratic Equations: Finding the Roots
The expression 4x² + 2x can be part of a quadratic equation, which is an equation of the form ax² + bx + c = 0, where 'a', 'b', and 'c' are constants. To solve a quadratic equation, we find the values of 'x' that make the equation true. These values are called the roots or solutions. There are several methods to solve quadratic equations, including factoring, the quadratic formula, and completing the square.
For example, if we set our expression equal to zero:
4x² + 2x = 0
We can factor out 2x:
2x(2x + 1) = 0
This equation is true if either 2x = 0 or 2x + 1 = 0. Solving for 'x', we find the roots: x = 0 and x = -1/2.
Applications: Where This Expression Appears
This seemingly simple algebraic expression has far-reaching applications in various fields:
Physics: Projectile Motion
Quadratic equations, like the one derived from our expression, are essential in physics for modeling projectile motion. The trajectory of a ball thrown in the air, for instance, can be described by a quadratic equation. The expression's variables would likely represent time, velocity, and acceleration.
Engineering: Designing Structures
Engineers use quadratic equations and related expressions to design structurally sound buildings and bridges. Understanding how forces and stresses are distributed requires complex calculations involving quadratic expressions.
Computer Science: Algorithms and Data Structures
In computer science, quadratic expressions can describe the time complexity of certain algorithms. This is crucial for optimizing program performance. For example, the time it takes to search through a sorted list can sometimes be represented by a quadratic equation.
Economics: Modeling Growth and Decay
Quadratic functions are also used to model economic phenomena, such as growth and decay of populations or investments.
Beyond the Basics: Exploring More Complex Scenarios
While we've focused on the core aspects of "x² + 2x + 3x²," this serves as a foundation for understanding more complex expressions. Consider the following:
- Adding more terms: The principles of combining like terms remain the same regardless of the number of terms in the expression.
- Higher-order polynomials: The same simplification methods can be extended to polynomials with higher powers of x (e.g., x³, x⁴, etc.).
- Multiple variables: Expressions can involve multiple variables (e.g., x, y, z), introducing further complexities and requiring advanced algebraic techniques.
Conclusion: Mastering the Fundamentals for Future Success
Understanding the expression "x² + 2x + 3x²," from its simplification to its applications, is a crucial stepping stone in mastering algebra and related mathematical fields. This guide provides a detailed exploration of its fundamental components, allowing you to not only solve this specific expression but also to tackle more complex algebraic problems with confidence. The ability to manipulate and interpret algebraic expressions is essential for success in numerous academic and professional pursuits. By understanding variables, exponents, like terms, factoring, and expanding, you equip yourself with the tools to conquer more challenging mathematical concepts and unlock a deeper appreciation for the elegance and power of algebra. Remember, practice is key! The more you work with these types of expressions, the more comfortable and proficient you'll become.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 2 2x 3 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.