X 2 X 1 2 Simplify
News Co
Mar 29, 2025 · 5 min read
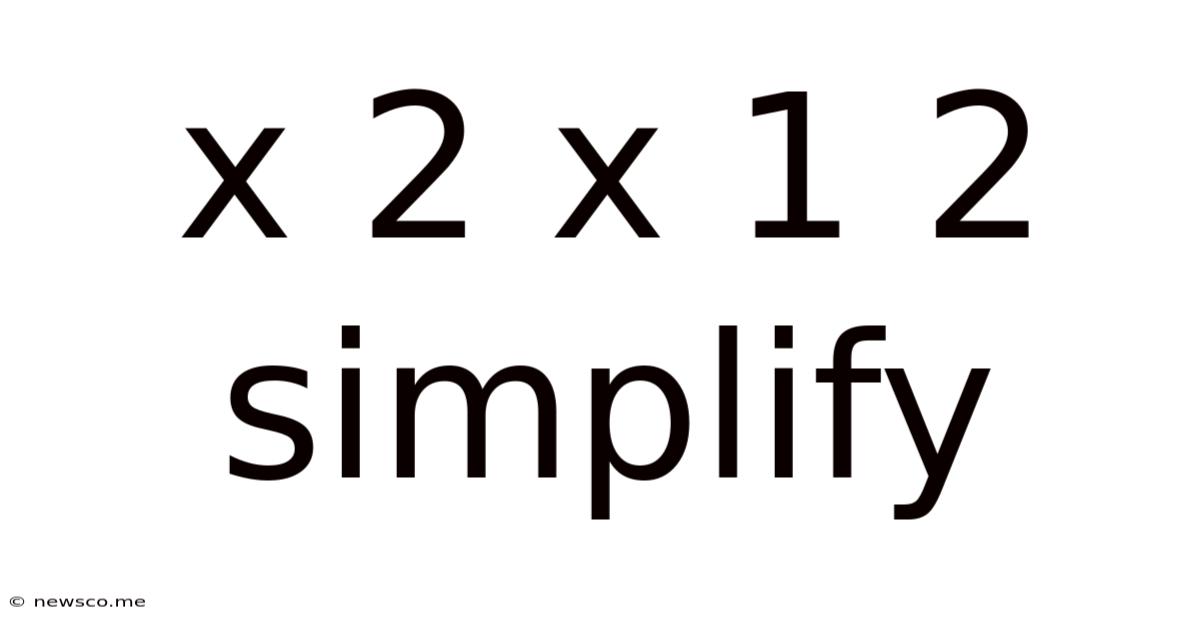
Table of Contents
Simplifying x²x¹²: A Comprehensive Guide to Algebraic Simplification
Simplifying algebraic expressions is a fundamental skill in mathematics. It allows us to manipulate equations, solve problems, and ultimately, understand the underlying relationships between variables. This article will delve deeply into simplifying the expression x²x¹², covering various methods, related concepts, and practical applications. We'll explore the rules of exponents, provide step-by-step solutions, and discuss common pitfalls to avoid. By the end, you'll possess a thorough understanding of how to handle similar expressions and apply these techniques to more complex algebraic problems.
Understanding the Rules of Exponents
Before we tackle the simplification of x²x¹², let's refresh our understanding of the fundamental rules of exponents. These rules govern how we operate with variables raised to powers. The key rules relevant to our problem are:
-
Product Rule: When multiplying two terms with the same base, we add their exponents. That is, a<sup>m</sup> * a<sup>n</sup> = a<sup>m+n</sup>. This is the core rule we'll use to simplify x²x¹².
-
Power of a Power Rule: When raising a power to another power, we multiply the exponents. That is, (a<sup>m</sup>)<sup>n</sup> = a<sup>mn</sup>.
-
Quotient Rule: When dividing two terms with the same base, we subtract the exponents. That is, a<sup>m</sup> / a<sup>n</sup> = a<sup>m-n</sup>.
-
Zero Exponent Rule: Any non-zero base raised to the power of zero equals 1. That is, a<sup>0</sup> = 1 (a ≠ 0).
-
Negative Exponent Rule: A base raised to a negative exponent is equal to the reciprocal of the base raised to the positive exponent. That is, a<sup>-n</sup> = 1/a<sup>n</sup> (a ≠ 0).
Simplifying x²x¹² using the Product Rule
Now, let's apply the product rule to simplify x²x¹². Recall that the product rule states that when multiplying terms with the same base, we add the exponents. In our case, the base is 'x' and the exponents are 2 and 12.
Therefore:
x²x¹² = x<sup>2+12</sup> = x<sup>14</sup>
The simplified form of x²x¹² is x¹⁴. This is the most concise and efficient way to represent the expression. It's crucial to understand that we're not changing the value of the expression; we're simply rewriting it in a more streamlined format.
Expanding the Concept: More Complex Examples
Let's extend our understanding by examining more complex scenarios involving similar simplification techniques.
Example 1: Simplify (2x³)(5x⁴)
Here, we'll combine the product rule with the understanding of multiplying coefficients (the numbers in front of the variables).
(2x³)(5x⁴) = (25)(x³x⁴) = 10x<sup>3+4</sup> = 10x⁷
Example 2: Simplify (3x²y)(4xy³)
This example introduces multiple variables. We apply the product rule separately to each variable.
(3x²y)(4xy³) = (34)(x²x)(y*y³) = 12x<sup>2+1</sup>y<sup>1+3</sup> = 12x³y⁴
Example 3: Simplify (x⁻²)(x⁵)
This introduces a negative exponent.
(x⁻²)(x⁵) = x<sup>-2+5</sup> = x³
Example 4: Simplify (2a²b³c)⁴
This utilizes the power of a power rule. Each factor within the parentheses is raised to the power of 4.
(2a²b³c)⁴ = 2⁴(a²)⁴(b³)⁴(c)⁴ = 16a⁸b¹²c⁴
These examples illustrate that the principles of simplifying expressions involving exponents are consistently applied, regardless of the complexity of the terms. Understanding the fundamental rules is key to handling increasingly intricate algebraic manipulations.
Common Mistakes to Avoid
Several common pitfalls can lead to incorrect simplifications. Let's address some of them:
-
Confusing multiplication with addition: Remember, when multiplying terms with the same base, you add the exponents, not multiply them. A common mistake is to write x²x¹² as x²⁴ instead of x¹⁴.
-
Incorrectly applying the power of a power rule: Remember to multiply the exponents when raising a power to another power, not add them.
-
Forgetting to apply the rule to all parts of the expression: When simplifying expressions with multiple terms and variables, ensure you apply the rules to each part consistently.
-
Neglecting coefficient multiplication: Don't forget to multiply the coefficients (numerical values) together when simplifying expressions containing both coefficients and variables.
Practical Applications and Real-World Relevance
The ability to simplify algebraic expressions isn't just an abstract mathematical exercise. It has widespread practical applications in various fields:
-
Physics: Many physical laws and equations are expressed algebraically. Simplifying these equations is crucial for problem-solving and understanding the relationships between different physical quantities (e.g., Newton's Law of Universal Gravitation).
-
Engineering: Engineers use algebraic simplification to design and analyze structures, circuits, and systems. Simplifying complex equations makes it easier to model real-world scenarios and predict outcomes.
-
Computer Science: Simplifying Boolean expressions is essential in optimizing computer programs and designing digital circuits.
-
Finance: Financial modeling often involves complex algebraic expressions that need to be simplified to make accurate predictions and manage risks.
-
Economics: Economic models rely heavily on algebraic manipulations. Simplifying equations makes it easier to analyze economic trends and forecast future economic outcomes.
Advanced Simplification Techniques
While the product rule effectively simplifies x²x¹², more advanced techniques become essential when dealing with more complex expressions. These include:
-
Factoring: This involves breaking down a complex expression into simpler factors. For example, factoring x² - 4 into (x-2)(x+2). This can be used to simplify rational expressions (fractions with algebraic terms).
-
Rationalizing the Denominator: This technique involves removing radicals (square roots, cube roots, etc.) from the denominator of a fraction.
-
Using Logarithms: Logarithms are useful for simplifying expressions with exponents, particularly when dealing with very large or very small numbers.
Conclusion
Simplifying algebraic expressions, such as x²x¹², is a crucial skill in mathematics and many other fields. Understanding the fundamental rules of exponents, particularly the product rule, is the cornerstone of this skill. By consistently applying these rules and avoiding common mistakes, you can confidently simplify complex expressions and unlock a deeper understanding of the mathematical relationships they represent. Remember to practice regularly to hone your skills and build confidence in tackling progressively challenging algebraic manipulations. This ability is not only beneficial for academic success but also provides a valuable skillset for many professional pursuits. The more you practice, the easier and more intuitive these simplifications will become. Mastering algebraic simplification opens up a world of opportunities to solve more intricate problems and explore the power of mathematical reasoning.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 2 X 1 2 Simplify . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.