X 2 X 2 X 1
News Co
Mar 24, 2025 · 5 min read
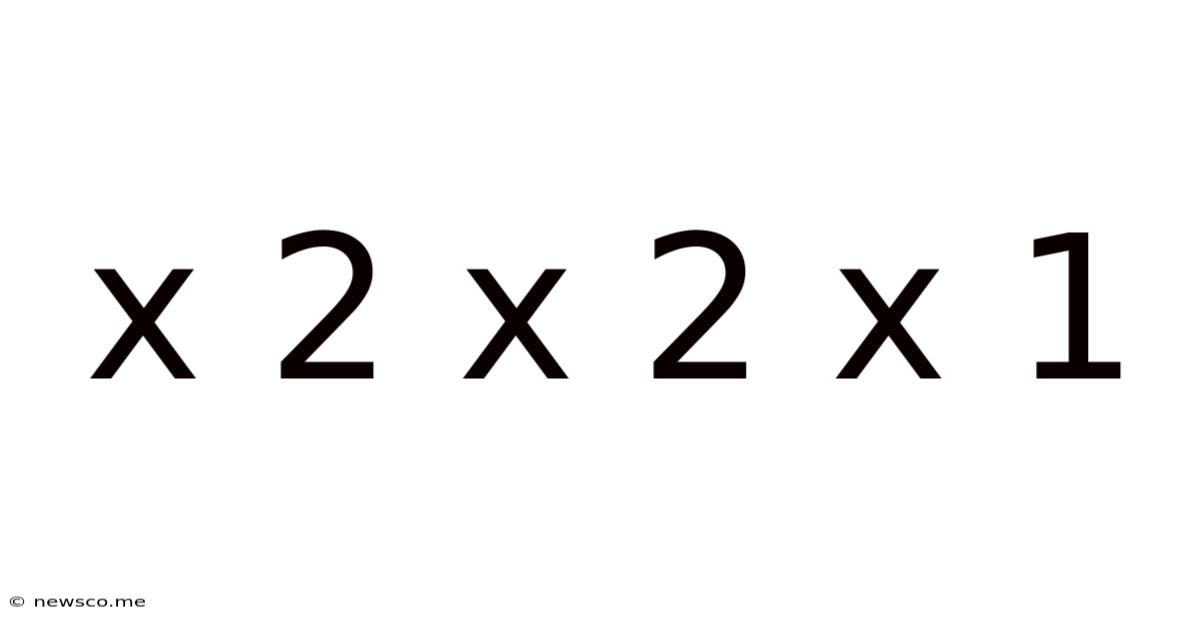
Table of Contents
Decoding the Enigma: A Deep Dive into the Dimensions of X x 2 x 2 x 1
The seemingly simple expression "x x 2 x 2 x 1" presents a fascinating challenge, opening doors to a surprising array of interpretations and applications across diverse fields. While mathematically straightforward, its true potential lies in its ability to serve as a foundational concept for exploring more complex ideas, from spatial dimensions and data structures to resource allocation and strategic planning. This article delves deep into this expression, unraveling its hidden complexities and illustrating its multifaceted relevance.
The Mathematical Core: Simple Multiplication, Profound Implications
At its most basic level, "x x 2 x 2 x 1" represents a simple multiplication problem. The value of 'x' acts as a variable, representing an unknown quantity. The expression simplifies to 4x. This straightforward calculation, however, forms the bedrock for exploring far more intricate concepts. Understanding this fundamental mathematical operation is crucial for comprehending its broader applications. We'll explore these applications in detail further down.
Why the seemingly simple is important: The elegance of this expression lies in its simplicity, making it easily accessible yet rich enough to model complex scenarios. This simplicity allows for easy scaling and modification, adapting the formula to fit various contexts. The constant multipliers (2, 2, and 1) provide a framework for structured expansion and analysis.
Exploring Dimensions: Visualizing X x 2 x 2 x 1
Consider "x" as representing a single unit. Then, "x x 2" can be visualized as a doubling of that unit along a single axis – a line segment expanding in length. "x x 2 x 2" expands this into a two-dimensional plane – a rectangle with dimensions 2x by 2x. Finally, "x x 2 x 2 x 1" introduces a third dimension, creating a rectangular prism (or cuboid) with dimensions 2x, 2x, and x.
This visualization allows us to connect the abstract mathematical expression to tangible spatial concepts. This connection provides an intuitive understanding of how scaling factors affect volume and area. It also forms a basis for understanding dimensional analysis – crucial in physics and engineering, where understanding units and their relationships is paramount.
Applications in Data Structures and Algorithms
The expression finds a home in the world of computer science, particularly in the design of data structures and algorithms. Imagine "x" representing the size of a basic data element. The multiplication factors then represent the expansion of this element in a multi-dimensional data structure.
Example 1: Arrays and Matrices: A one-dimensional array can be represented as 'x'. A two-dimensional array (matrix) could be represented as 'x x 2 x 2', indicating a square matrix. This is a crucial concept in linear algebra and computer graphics.
Example 2: Tree Structures: In a binary tree structure, 'x' could represent a single node. Each multiplication by 2 could represent branching to two child nodes, leading to an exponential increase in the total number of nodes.
Resource Allocation and Optimization
In operational research and management, "x x 2 x 2 x 1" can model various resource allocation problems. Consider 'x' representing a basic unit of resource (e.g., time, manpower, or budget). The multipliers then represent the scaling of resource allocation across different factors.
Example 1: Project Management: If 'x' represents the initial project effort, then 'x x 2 x 2 x 1' might represent an expansion in scope across different project phases, indicating an overall increase in resource requirements.
Example 2: Inventory Management: 'x' could represent the initial stock level of a particular item. The multipliers might reflect increasing demand over different periods, requiring more stock to be held.
Strategic Planning and Scaling: Growth Models and Expansion
The expression can be a valuable tool for modeling growth and expansion strategies. Starting with a basic unit of operation ('x'), the multipliers demonstrate a systematic increase in scale. This allows for analyzing the impact of expanding operations, assessing potential challenges, and optimizing resource allocation for growth.
Example 1: Business Expansion: 'x' could represent the initial market size. 'x x 2 x 2 x 1' could model an expansion into new markets (x2), increased product lines (x2), and increased production efficiency (x1).
Example 2: Population Growth: In simplified population models, 'x' could represent the initial population size. The multipliers can model factors influencing population growth such as birth rates, migration, and resource availability.
Beyond the Numbers: The Power of Abstraction
The true power of "x x 2 x 2 x 1" lies not just in its mathematical precision but in its capacity for abstract representation. It serves as a framework for modeling various systems and processes, facilitating analysis, prediction, and optimization. By substituting 'x' with different variables and adjusting the multipliers, the expression adapts to a vast array of applications. This adaptable nature makes it a versatile tool for problem-solving across numerous domains.
Exploring Variations and Extensions
The basic expression can be further extended and modified to model even more complex scenarios:
- Introducing different multipliers: Instead of 2, 2, and 1, different multipliers can be used to represent varied scaling factors.
- Adding exponents: Raising the multipliers to exponents can model exponential growth or decay.
- Introducing multiple variables: Replacing 'x' with multiple variables can represent systems with multiple interacting factors.
These modifications make the expression even more powerful, allowing for the creation of sophisticated models reflecting real-world complexities.
Conclusion: Unlocking the Potential of Simplicity
The seemingly simple expression "x x 2 x 2 x 1" reveals its remarkable versatility and depth upon closer examination. Its simplicity makes it an easily understood foundation for more complex concepts, bridging the gap between abstract mathematics and real-world applications. From visualizing spatial dimensions to modeling resource allocation and strategic planning, its adaptability makes it a powerful tool for problem-solving and analysis across a multitude of disciplines. By understanding its core principles and exploring its variations, we can unlock its potential to create more robust, efficient, and insightful models in our quest for knowledge and innovation. The expression's enduring appeal lies in its capacity to be both a simple starting point and a pathway to far-reaching explorations. The journey of understanding its multifaceted potential is an ongoing process, inviting further exploration and innovative applications. The simplicity of its form belies the complexity of its implications, making it a truly fascinating subject for continued study and analysis.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 2 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.