X 3 1 7 15 Solve The Equation
News Co
Apr 10, 2025 · 5 min read
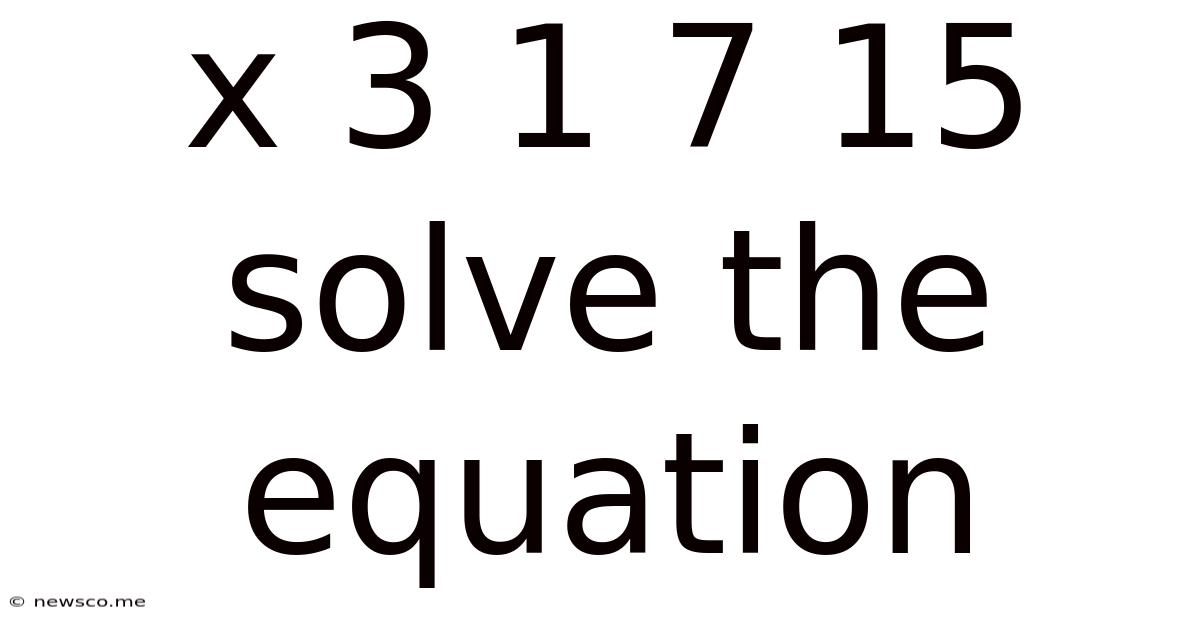
Table of Contents
Decoding the Enigma: Exploring Solutions to the Equation x³ + 1 = 7x + 15
This article delves deep into the mathematical puzzle presented by the equation x³ + 1 = 7x + 15. We'll explore various methods to solve this cubic equation, examining both numerical and analytical approaches. Understanding this equation involves more than just finding the solution; it's about grasping the underlying principles of algebra and numerical methods. We will uncover the significance of each step and explore potential avenues for similar problem-solving.
Understanding the Problem: A Cubic Equation
The equation x³ + 1 = 7x + 15 is a cubic equation, meaning the highest power of the variable 'x' is 3. Cubic equations, unlike linear or quadratic equations, can have up to three real solutions (or roots). These solutions represent the x-values where the left-hand side (LHS) of the equation equals the right-hand side (RHS). Our task is to find these x-values.
Before diving into the solution methods, let's rearrange the equation into its standard form:
x³ - 7x - 14 = 0
This standard form, where all terms are on one side and equal to zero, is crucial for many solution techniques.
Method 1: The Rational Root Theorem
The Rational Root Theorem is a valuable tool for finding potential rational solutions (solutions that are fractions or integers). It states that any rational root of a polynomial equation with integer coefficients can be expressed as p/q, where 'p' is a factor of the constant term and 'q' is a factor of the leading coefficient.
In our equation, x³ - 7x - 14 = 0:
- The constant term is -14. Its factors are ±1, ±2, ±7, ±14.
- The leading coefficient is 1. Its factors are ±1.
Therefore, the potential rational roots are ±1, ±2, ±7, ±14. We can test these values by substituting them into the equation.
Let's try some:
- x = 1: 1³ - 7(1) - 14 = -20 ≠ 0
- x = -1: (-1)³ - 7(-1) - 14 = -8 ≠ 0
- x = 2: 2³ - 7(2) - 14 = -18 ≠ 0
- x = -2: (-2)³ - 7(-2) - 14 = -8 ≠ 0
- x = 7: 7³ - 7(7) - 14 = 294 ≠ 0
- x = -7: (-7)³ - 7(-7) - 14 = -294 ≠ 0
- x = 14: 14³ - 7(14) - 14 = 2646 ≠ 0
- x = -14: (-14)³ - 7(-14) - 14 = -2646 ≠ 0
None of the potential rational roots satisfy the equation. This indicates that the equation likely has irrational roots or complex roots (involving the imaginary unit 'i').
Method 2: Numerical Methods – The Bisection Method
Since the Rational Root Theorem didn't yield a solution, we turn to numerical methods. The Bisection Method is a relatively simple iterative method that approximates the root of an equation. It requires finding an interval [a, b] where the function changes sign, indicating a root lies within the interval.
Let's define our function: f(x) = x³ - 7x - 14
Let's try some intervals:
- f(2) = -18
- f(3) = 2 There is a sign change between x = 2 and x = 3, indicating a root lies in this interval.
The Bisection Method repeatedly bisects this interval and checks the sign of the function at the midpoint. This process continues until the desired accuracy is achieved. While we won't perform the iterative calculations here, this method would converge towards one of the real roots.
Method 3: Numerical Methods – Newton-Raphson Method
The Newton-Raphson Method is another iterative numerical method, generally faster than the Bisection Method but requiring the derivative of the function. The iterative formula is:
x_(n+1) = x_n - f(x_n) / f'(x_n)
Where:
- x_n is the current approximation of the root
- x_(n+1) is the next approximation
- f(x_n) is the function value at x_n
- f'(x_n) is the derivative of the function at x_n
For our function, f(x) = x³ - 7x - 14, the derivative is f'(x) = 3x² - 7.
Starting with an initial guess (e.g., x₀ = 3), we can iteratively apply the formula to refine the approximation of the root. Again, the detailed iterative calculations are beyond the scope of this discussion, but this method would also converge to a real root.
Method 4: Cardano's Method (for Cubic Equations)
Cardano's Method provides an analytical solution for cubic equations. However, it's a complex process involving several steps and substitutions. This method is less practical for manual calculation, especially with more complex coefficients. It's generally more suited for symbolic manipulation software.
The method involves transforming the cubic equation into a depressed cubic (one without the x² term) and then using specific formulas to obtain the roots. Due to its complexity, we will not detail the steps here.
Understanding the Nature of Roots
After employing numerical methods like the Bisection or Newton-Raphson methods, you'll find that the equation x³ - 7x - 14 = 0 possesses one real root and two complex conjugate roots. This is a common characteristic of cubic equations. The real root will be an approximation (since numerical methods provide approximations), while the complex roots will involve the imaginary unit 'i'.
Significance and Applications
Solving cubic equations like this one is not just an academic exercise. Cubic equations appear in various real-world applications, including:
- Engineering: Designing structures, calculating fluid flow, analyzing electrical circuits.
- Physics: Modeling trajectories, solving problems in mechanics and thermodynamics.
- Computer graphics: Creating smooth curves and surfaces.
- Economics: Modeling growth and decay processes.
Understanding how to solve these equations, whether through numerical methods or (for simpler cases) analytical methods, is fundamental to solving problems in these fields.
Conclusion: A Multifaceted Problem
Solving the equation x³ + 1 = 7x + 15 demonstrates the power and versatility of different mathematical approaches. While the Rational Root Theorem failed to provide an immediate solution, numerical methods like the Bisection and Newton-Raphson methods provide accurate approximations of the real root. Understanding the nature of roots – in this case, one real and two complex conjugate roots – is crucial to fully comprehending the solution. The complexity of Cardano's method highlights the need for numerical approaches in many practical scenarios. Mastering these techniques equips you with valuable problem-solving skills applicable to a vast array of scientific and engineering disciplines. The journey to understanding this seemingly simple equation unveils the rich tapestry of mathematical concepts and techniques that underpin problem-solving in the real world.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 3 1 7 15 Solve The Equation . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.