X 3 3x 2 2x 6
News Co
Apr 24, 2025 · 4 min read
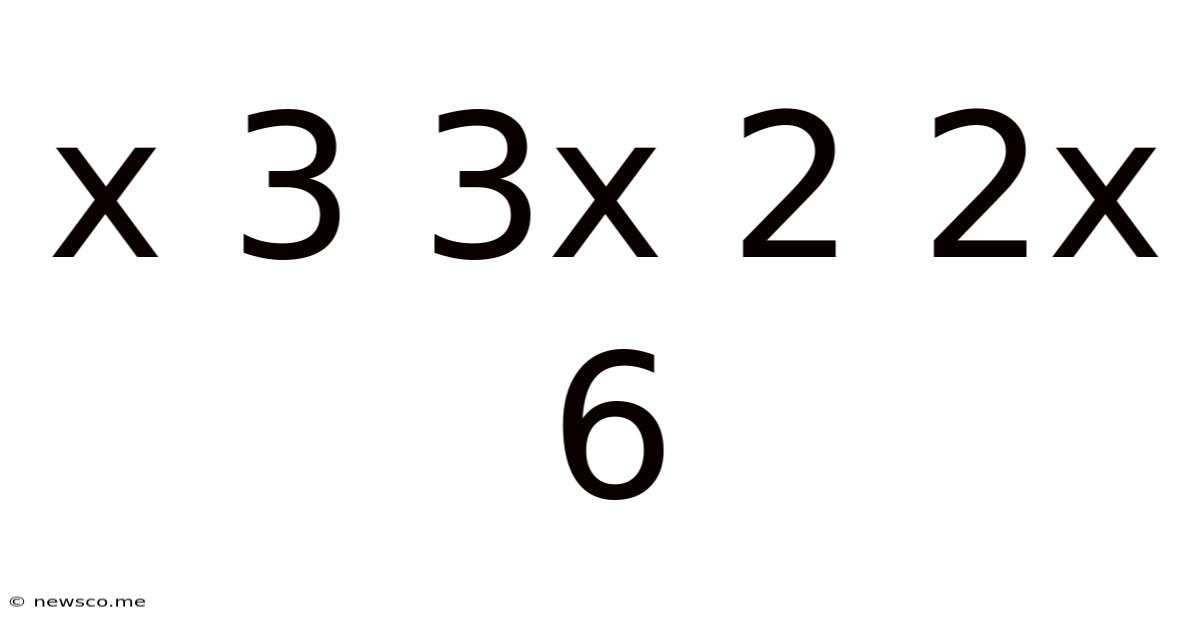
Table of Contents
Decoding the Mathematical Puzzle: x³ + 3x² + 2x + 6
This article delves into the mathematical expression x³ + 3x² + 2x + 6, exploring its properties, potential solutions, and the broader mathematical concepts it embodies. We'll dissect various approaches to analyzing this cubic polynomial, including factoring techniques, graphical representations, and numerical methods. The aim is to provide a comprehensive understanding, accessible to a wide range of readers, from high school students to those revisiting their mathematical foundations.
Understanding Cubic Polynomials
Before we tackle the specifics of x³ + 3x² + 2x + 6, let's establish a foundational understanding of cubic polynomials. A cubic polynomial is a polynomial of degree three, meaning the highest power of the variable (in this case, x) is three. The general form is given by:
ax³ + bx² + cx + d = 0
Where a, b, c, and d are constants, and 'a' is not equal to zero. Our specific polynomial, x³ + 3x² + 2x + 6, fits this general form with a=1, b=3, c=2, and d=6.
Methods for Solving Cubic Polynomials
Solving cubic polynomials can be more challenging than solving linear or quadratic equations. There isn't a single, universally simple formula like the quadratic formula. However, several methods exist, each with its own strengths and limitations:
1. Factoring
Factoring is the most straightforward method if it's possible. We look for common factors among the terms. In our case, x³ + 3x² + 2x + 6, there aren't any immediate common factors among all terms. However, we can attempt to factor by grouping:
x²(x + 3) + 2(x + 3)
Notice that (x + 3) is a common factor, allowing us to factor further:
(x + 3)(x² + 2) = 0
This factorization reveals one real root: x = -3. The quadratic factor, x² + 2, yields two complex roots: x = ±√(-2) = ±i√2.
2. The Rational Root Theorem
The Rational Root Theorem helps identify potential rational roots (roots that are fractions of integers) of a polynomial. It states that if a polynomial has a rational root p/q (where p and q are integers and q ≠ 0), then p must be a factor of the constant term (d) and q must be a factor of the leading coefficient (a).
In our polynomial, x³ + 3x² + 2x + 6, the constant term is 6 and the leading coefficient is 1. Therefore, the potential rational roots are the factors of 6: ±1, ±2, ±3, ±6. Testing these values, we find that x = -3 is a root, consistent with our factoring result.
3. Numerical Methods
When factoring proves difficult or impossible, numerical methods offer approximate solutions. These methods involve iterative processes to refine an initial guess until a root is found to a desired level of accuracy. Common numerical methods for finding roots of polynomials include:
- Newton-Raphson Method: This iterative method uses the derivative of the polynomial to refine the approximation of the root.
- Bisection Method: This method repeatedly halves an interval known to contain a root, until the desired accuracy is achieved.
4. Graphical Representation
Plotting the polynomial as a function, y = x³ + 3x² + 2x + 6, provides a visual representation of its behavior. The x-intercepts of the graph represent the real roots of the polynomial. Using graphing software or a calculator, we can visually confirm the real root at x = -3 and observe that there are no other x-intercepts, indicating the other roots are complex.
Interpreting the Results and Significance
The polynomial x³ + 3x² + 2x + 6 has one real root (x = -3) and two complex roots (x = i√2 and x = -i√2). The presence of complex roots is common in cubic (and higher-degree) polynomials. Complex numbers extend the number system beyond real numbers, enabling the solution of equations that wouldn't have solutions within the realm of real numbers alone.
Applications of Cubic Polynomials
Cubic polynomials have numerous applications in various fields:
- Engineering: They are used in modeling the behavior of structures, calculating fluid flow, and designing various mechanical systems.
- Physics: Cubic equations arise in problems involving projectile motion, oscillations, and wave phenomena.
- Economics: They can be used in modeling economic growth, cost functions, and other economic relationships.
- Computer Graphics: Cubic curves are frequently used in computer-aided design and animation to create smooth curves and surfaces.
Advanced Considerations
For more advanced explorations, one can delve into:
- Cubic Formula: While complex, a general formula exists for solving cubic equations, analogous to the quadratic formula.
- Cardano's Method: This historical method provides a systematic approach to solving cubic equations.
- Complex Analysis: A deeper understanding of complex numbers and their properties provides further insights into the nature of complex roots.
Conclusion
The seemingly simple expression x³ + 3x² + 2x + 6 offers a gateway to a rich landscape of mathematical concepts. By employing various methods – factoring, the Rational Root Theorem, numerical techniques, and graphical analysis – we can thoroughly analyze this cubic polynomial, unveiling its real and complex roots. Understanding cubic polynomials, and their solution methods, is essential for anyone pursuing studies or careers in mathematics, science, and engineering. The principles explored here extend to higher-degree polynomials, highlighting the power and elegance of algebraic techniques. The ability to solve such equations is crucial for numerous applications across diverse fields, demonstrating the practical relevance of seemingly abstract mathematical concepts. Further exploration into the advanced topics mentioned above can provide even deeper insight into the intricacies of cubic polynomials and their profound impact on numerous disciplines.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 3 3x 2 2x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.