X 3 3x 2 3x 1
News Co
Apr 24, 2025 · 5 min read
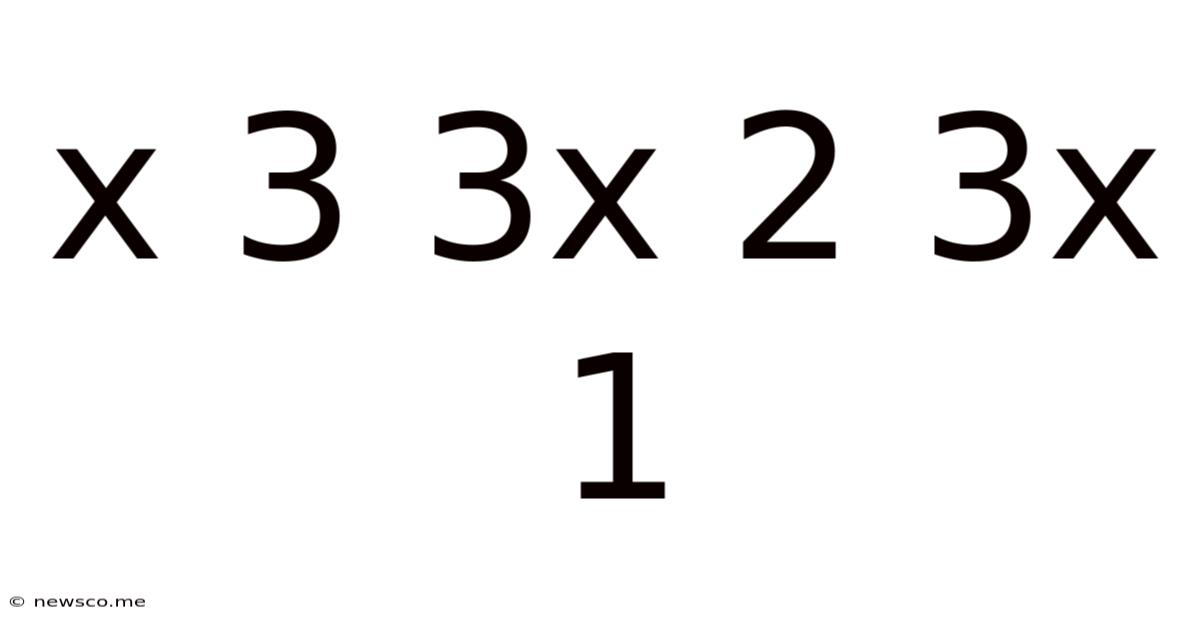
Table of Contents
Decoding the Mystery: A Deep Dive into x³ + 3x² + 3x + 1
The expression x³ + 3x² + 3x + 1 might seem like a simple algebraic equation, but it holds a significant position in mathematics and has far-reaching applications across various fields. This seemingly straightforward polynomial is, in fact, a perfect cube expansion, and understanding its properties and implications unlocks a deeper understanding of algebraic structures and their practical uses. This article will explore this fascinating expression in detail, examining its derivation, its relationship to the binomial theorem, its graphical representation, and its applications in various areas, including calculus, physics, and computer science.
Understanding the Perfect Cube Expansion
At its core, x³ + 3x² + 3x + 1 is a perfect cube expansion. It represents the expansion of (x + 1)³. This can be easily verified using the binomial theorem, or through manual multiplication:
(x + 1)(x + 1)(x + 1) = (x² + 2x + 1)(x + 1) = x³ + x² + 2x² + 2x + x + 1 = x³ + 3x² + 3x + 1
This expansion demonstrates a fundamental concept in algebra: the ability to simplify complex expressions into more manageable forms. This simplification is crucial for solving equations, simplifying calculations, and identifying patterns in mathematical relationships.
The Binomial Theorem and its Relevance
The binomial theorem provides a powerful and general method for expanding expressions of the form (a + b)^n. For the case of (x + 1)³, the binomial theorem states:
(x + 1)³ = ³C₀x³(1)⁰ + ³C₁x²(1)¹ + ³C₂x¹(1)² + ³C₃x⁰(1)³
Where ³Cₓ represents the binomial coefficient, calculated as n!/(k!(n-k)!). Applying this formula, we get:
(x + 1)³ = 1x³ + 3x² + 3*x + 1 = x³ + 3x² + 3x + 1
This confirms our earlier result and highlights the elegance and efficiency of the binomial theorem in handling such expansions. Understanding the binomial theorem is crucial for working with higher-order polynomial expansions and exploring various combinatorial problems.
Graphical Representation and its Insights
Visualizing the equation x³ + 3x² + 3x + 1 graphically provides valuable insights into its behavior and properties. Plotting this cubic function reveals a monotonically increasing curve. This means that the function's value continuously increases as the value of x increases. There are no local maxima or minima, and the curve smoothly progresses without any turning points. The function's y-intercept is at (0,1), and its root is at x = -1.
Analyzing the Curve's Behavior
The monotonically increasing nature of the curve indicates a consistent and predictable relationship between x and the function's output. This property has implications in various applications where understanding the rate of change is critical. For example, in modeling population growth or the spread of a disease, such consistently increasing functions are frequently employed.
The single root at x = -1 signifies that the function intersects the x-axis only once. This is a characteristic feature of cubic equations that have only one real root. The other two roots are complex conjugates, not visible on a standard real-number graph.
Applications Across Diverse Fields
The expression x³ + 3x² + 3x + 1, while seemingly simple, finds applications in a wide range of fields:
1. Calculus and Differential Equations:
In calculus, this expression can be easily differentiated and integrated. Its derivative, 3x² + 6x + 3, provides information about the rate of change of the original function. Its integral provides information about the area under the curve. These derivatives and integrals are fundamental tools for analyzing rates of change and accumulation in various scientific and engineering problems.
2. Physics and Engineering:
Cubic equations, such as x³ + 3x² + 3x + 1, frequently appear in various physical phenomena. For example, they can model the trajectory of a projectile, the displacement of a vibrating system, or the flow of fluids in certain contexts. Solving such equations is crucial for accurately predicting the behavior of these systems.
3. Computer Science and Algorithm Analysis:
In computer science, polynomial expressions are used to analyze the efficiency of algorithms. The degree of the polynomial often reflects the time complexity of an algorithm. Understanding polynomial expansions is essential for developing efficient algorithms and optimizing software performance.
4. Financial Modeling:
In finance, cubic equations can sometimes be used to model compound interest, growth rates, or the value of assets over time. These models allow financial analysts to predict future values and make informed decisions.
Beyond the Basics: Exploring Generalizations
The expression x³ + 3x² + 3x + 1 is a specific case of a broader family of perfect cube expansions. The general form of a perfect cube expansion is:
(a + b)³ = a³ + 3a²b + 3ab² + b³
Our original expression is simply a specialized case where a = x and b = 1. This generalization allows us to expand and simplify a wider range of expressions and apply similar analytical techniques.
Exploring Variations and Extensions
We can explore variations by changing the coefficients or by introducing other variables. For example, we could investigate the properties of (2x + 1)³ or (x + 2)³, which will produce different cubic polynomials, but still share the underlying structure of a perfect cube expansion. These variations lead to a better understanding of the general behavior of cubic equations.
Conclusion: A Simple Expression with Profound Implications
While x³ + 3x² + 3x + 1 appears to be a relatively straightforward algebraic expression, it serves as a gateway to understanding deeper mathematical concepts. From the binomial theorem to its applications in various scientific and technological fields, this expression demonstrates the interconnectedness of mathematical ideas and their practical relevance in the world around us. Its exploration encourages a deeper appreciation of the power and elegance of mathematical structures and their capacity to model complex phenomena with remarkable accuracy and efficiency. Further investigation into its properties, variations, and applications opens up a world of possibilities for mathematical exploration and problem-solving. The seemingly simple equation holds a wealth of knowledge and provides a solid foundation for more advanced mathematical studies.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 3 3x 2 3x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.