X 3 3x 2 X 1
News Co
Apr 12, 2025 · 5 min read
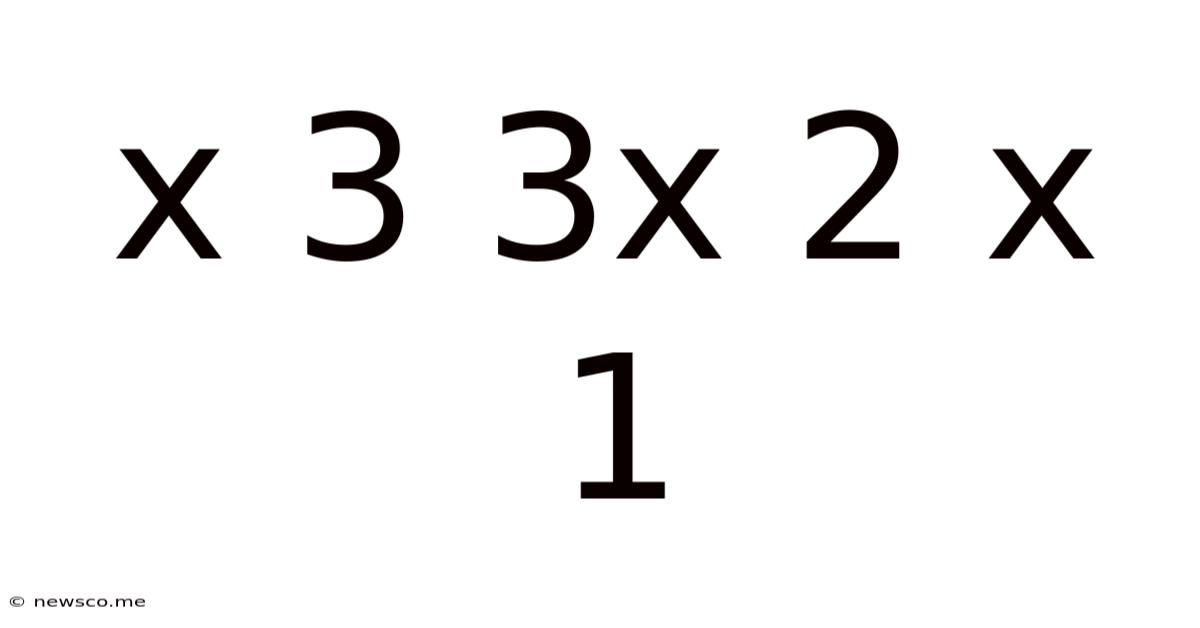
Table of Contents
Decoding the Enigma: A Deep Dive into x³ + 3x² + 2x + 1
The seemingly simple polynomial expression, x³ + 3x² + 2x + 1, hides a wealth of mathematical richness. This seemingly innocuous equation opens doors to a variety of mathematical concepts, from basic algebra to advanced calculus and even touches upon the fascinating world of abstract algebra. This article will explore this cubic polynomial in depth, examining its properties, solutions, applications, and its place within broader mathematical contexts.
Understanding the Basics: Polynomial Structure and Terminology
Before delving into the specifics of x³ + 3x² + 2x + 1, let's establish a foundational understanding of polynomials. A polynomial is an expression consisting of variables (in this case, 'x') and coefficients, combined using addition, subtraction, and multiplication, but never division by a variable. The highest power of the variable is known as the degree of the polynomial. In our equation, x³ + 3x² + 2x + 1, the degree is 3, making it a cubic polynomial.
- Coefficients: The numbers preceding each term (3, 2, and 1) are the coefficients. They dictate the scaling of each power of x.
- Terms: Each part of the polynomial separated by a plus or minus sign is a term. (x³, 3x², 2x, and 1)
- Constant Term: The term without a variable (1 in this case) is called the constant term.
Finding the Roots (Solutions): Methods and Interpretations
Finding the roots, or zeros, of a polynomial means determining the values of x that make the polynomial equal to zero. For our cubic polynomial, this means solving the equation:
x³ + 3x² + 2x + 1 = 0
Unfortunately, there's no straightforward algebraic formula for finding the roots of all cubic equations like there is for quadratic equations (using the quadratic formula). However, several methods can be employed:
1. Numerical Methods: Approximating the Roots
For cubic polynomials that lack easily identifiable rational roots, numerical methods are often employed. These methods use iterative processes to approximate the roots to a desired degree of accuracy. Examples include:
- Newton-Raphson Method: This iterative technique refines an initial guess for a root using the function's derivative.
- Bisection Method: This method repeatedly divides an interval containing a root in half, narrowing down the location of the root.
2. Graphical Methods: Visualizing the Roots
Plotting the function y = x³ + 3x² + 2x + 1 allows for a visual identification of the x-intercepts (points where the graph crosses the x-axis). These x-intercepts represent the real roots of the polynomial. While graphical methods don't provide exact values, they offer a valuable initial understanding of the roots' approximate locations.
3. Rational Root Theorem: Checking for Rational Roots
The Rational Root Theorem states that any rational root of a polynomial with integer coefficients must be of the form p/q, where p is a factor of the constant term and q is a factor of the leading coefficient. In our case:
- Constant term: 1 (factors are ±1)
- Leading coefficient: 1 (factors are ±1)
Therefore, the only possible rational roots are ±1. Testing these values:
- If x = 1: 1³ + 3(1)² + 2(1) + 1 = 7 ≠ 0
- If x = -1: (-1)³ + 3(-1)² + 2(-1) + 1 = 1 ≠ 0
This indicates that our polynomial doesn't have rational roots.
4. Cubic Formula: The General Solution
While more complex than the quadratic formula, a general cubic formula exists for finding the roots of any cubic equation. This formula, however, is quite cumbersome and often involves complex numbers even when the polynomial has only real roots. It is rarely used in practice for manual calculations due to its complexity.
Analyzing the Polynomial's Behavior: Derivatives and Inflection Points
Understanding the behavior of the polynomial is crucial for interpreting its roots and overall shape. Calculus provides the tools to do this:
1. The First Derivative: Slope and Critical Points
The first derivative, f'(x), gives the slope of the tangent line at any point on the curve. For our polynomial:
f'(x) = 3x² + 6x + 2
Setting f'(x) = 0 allows us to find the critical points, where the slope is zero (potential local maxima or minima).
Solving 3x² + 6x + 2 = 0 using the quadratic formula yields two real roots, indicating the presence of a local minimum and a local maximum.
2. The Second Derivative: Concavity and Inflection Points
The second derivative, f''(x), provides information about the concavity of the curve. For our polynomial:
f''(x) = 6x + 6
Setting f''(x) = 0 helps determine inflection points, where the concavity changes. In this case, f''(x) = 0 when x = -1. This means the curve changes from concave down to concave up at x = -1.
Applications of Cubic Polynomials: Real-World Relevance
Cubic polynomials, despite their seemingly abstract nature, have numerous applications across various fields:
- Engineering: Designing curves for roads, bridges, and roller coasters often involves cubic functions to ensure smooth transitions.
- Physics: Modeling the trajectory of projectiles, the motion of objects under certain forces, and the behavior of certain physical systems.
- Economics: Analyzing cost functions, revenue functions, and profit maximization problems.
- Computer Graphics: Creating smooth curves and surfaces in computer-aided design (CAD) and 3D modeling.
Extending the Concepts: Complex Numbers and Beyond
The solutions to cubic equations can involve complex numbers, numbers of the form a + bi, where 'a' and 'b' are real numbers, and 'i' is the imaginary unit (√-1). The presence of complex roots adds another layer of complexity to the analysis of cubic polynomials, but it is essential for a complete understanding of their behavior.
Furthermore, understanding cubic polynomials provides a stepping stone to exploring higher-degree polynomials and more abstract algebraic concepts, such as field extensions and Galois theory.
Conclusion: The Enduring Significance of x³ + 3x² + 2x + 1
The seemingly simple polynomial x³ + 3x² + 2x + 1 serves as a microcosm of the broader field of mathematics. Its analysis requires a blend of algebraic techniques, calculus, and numerical methods, showcasing the interconnectedness of different mathematical areas. Its applications span diverse fields, highlighting the practical relevance of abstract mathematical concepts. By delving into this seemingly simple equation, we've uncovered a wealth of mathematical richness and its significant impact on our understanding of the world around us. The journey of exploring this cubic polynomial is a testament to the beauty and power of mathematics, revealing layers of complexity and elegance within a simple expression.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 3 3x 2 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.