X 3 4x 2 9x 36
News Co
Apr 25, 2025 · 5 min read
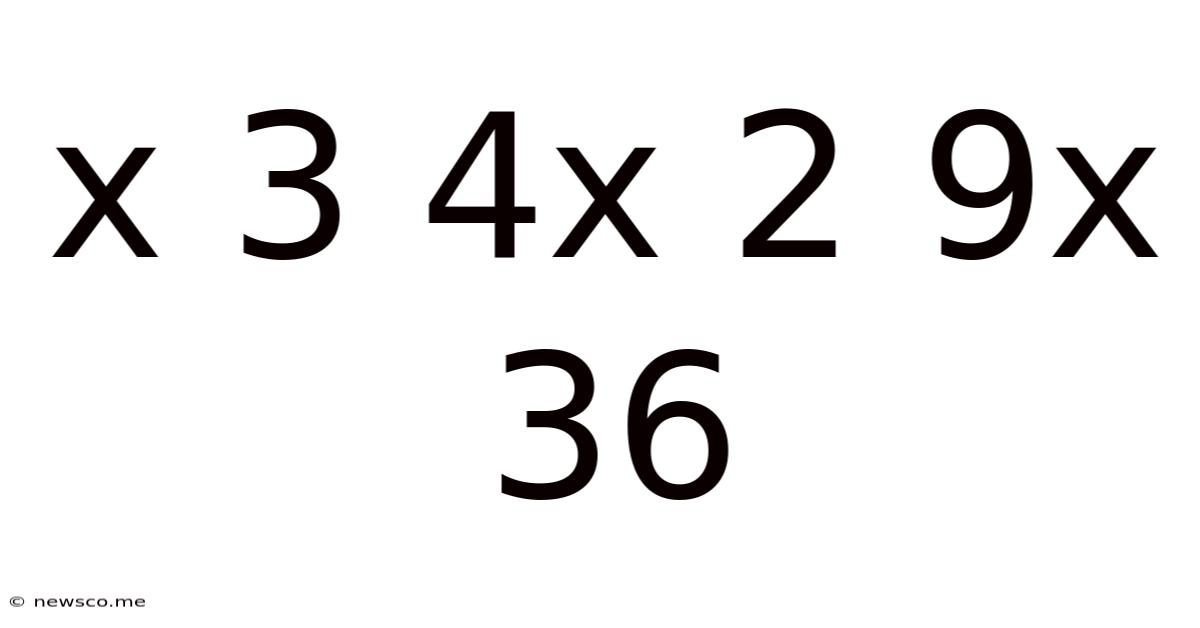
Table of Contents
Decoding the Pattern: Exploring the Mathematical Sequence x 3, 4x, 2, 9x, 36
The seemingly simple sequence "x 3, 4x, 2, 9x, 36" presents a fascinating challenge: deciphering the underlying mathematical logic and predicting subsequent terms. This article will delve deep into this sequence, exploring potential patterns, applying mathematical principles, and ultimately, offering possible solutions and extensions. We'll consider different perspectives, from simple arithmetic progressions to more intricate geometric and recursive relationships.
Identifying Potential Patterns: A Step-by-Step Approach
At first glance, the sequence might seem random. However, a closer inspection reveals the presence of both multiplication and, potentially, a hidden pattern related to the numbers 3 and 4. Let's break down the sequence to uncover potential relationships:
- x 3: This term clearly involves multiplication by 3.
- 4x: This term involves multiplication by 4.
- 2: This term appears to be an outlier, deviating from the multiplication pattern.
- 9x: This term uses multiplication by 9, a square of 3.
- 36: This term is 6 squared (6 x 6), and notably 4 x 9.
The Role of Multiplication
The prominent use of multiplication in several terms suggests a strong mathematical connection. The multipliers 3, 4, and 9 themselves display an interesting relationship. We see that 9 is the square of 3, and 4 lies between 3 and 9. This observation might indicate a sequential pattern of multipliers, potentially involving squares or powers.
Investigating the Outlier: The Significance of "2"
The inclusion of "2" as a seemingly independent term requires careful consideration. It's crucial to explore how it might fit into the overall pattern. Could it represent a specific operation, a break in the sequence, or even an error? Several hypotheses could explain its presence:
- Alternating Pattern: Perhaps the sequence alternates between two distinct types of operations: multiplication by a specific number and another, independent operation. This might explain the appearance of "2" which doesn't neatly fit the multiplication pattern.
- Remainder or Residue: The number "2" could be the result of a calculation involving the preceding and/or following terms. Finding this link would unlock a deeper understanding of the pattern.
- A Separate Sequence: It's possible that the sequence is not a single coherent mathematical pattern, but rather a combination of two or more intertwining sequences. The "2" might belong to a separate pattern occurring at specific intervals.
Advanced Analysis: Exploring Potential Mathematical Functions
To unravel the complexities of this sequence, we can explore more advanced mathematical concepts:
Recursive Relationships
A recursive relationship defines a sequence where each term is dependent on the preceding ones. While it's difficult to definitively establish a simple recursive relationship for the given sequence, we can explore potential formulations. For instance, a recursive function could consider the previous terms, calculating the next based on a combination of operations. A more complicated relationship could account for "2" as a special case, modifying the rules when encountering this term.
Geometric Progressions
Geometric progressions involve a constant multiplier between successive terms. While the sequence "x 3, 4x, 2, 9x, 36" doesn't perfectly fit this model due to the presence of "2," a geometric progression could form a sub-sequence within the larger sequence. This might mean we are dealing with two separate patterns interwoven.
Polynomial Relationships
A more complex approach involves fitting a polynomial function to the data points of the sequence. By representing the sequence as a set of (n, a_n) pairs, where n is the position and a_n is the term, we could try to find a polynomial of degree n that perfectly fits (or closely approximates) this data. However, the "x" variable makes this approach more challenging as it must be incorporated into the polynomial's independent variable.
Constructing Possible Solutions and Extensions
Based on the analysis, several hypotheses can explain the sequence, offering various ways to predict future terms:
Hypothesis 1: The Alternating Pattern
This hypothesis suggests alternating between multiplication by an increasing power of 3 and a separate function producing the term "2". This produces the following sequence:
- x3
- 4x
- 2
- 9x
- 36
- 2 (or another term if a different pattern emerges for the second alternating sequence)
- 27x
- ...and so on
Hypothesis 2: The Intertwined Sequence
This hypothesis proposes two intertwined sequences: one based on multiples of x and the other an independent sequence. The sequence might continue with an independent term (not necessarily "2"), followed by 27x, and another independent term, and so forth. This requires further investigation to identify the pattern of the independent sequence.
Hypothesis 3: The Modified Geometric Progression
This approach modifies the geometric progression concept. We could consider a geometric progression for the multiples of "x," creating a sub-sequence: x3, 9x, 27x, 81x, etc. This leaves the sequence of the other terms (4x, 2, 36,...) to be identified as the second sub-sequence.
Conclusion: The Importance of Context and Further Investigation
The sequence "x 3, 4x, 2, 9x, 36" offers a rich problem illustrating the multifaceted nature of mathematical pattern recognition. Without additional context or information, pinpointing a single definitive solution remains challenging. The lack of clarity around the nature of "x" itself further complicates this. If "x" is a specific constant, it would vastly simplify the possibilities. If it's a variable within a wider mathematical context, additional equations or conditions could unlock the sequence's true nature.
Further investigation might involve:
- Additional Terms: More terms in the sequence would provide more data points, allowing for a more robust analysis and the possibility of definitively identifying the underlying pattern.
- Contextual Information: Understanding the origin or context of the sequence would be crucial. If it's part of a larger mathematical problem, this could provide valuable clues.
- Alternative Interpretations: It's crucial to consider alternative interpretations of the sequence's symbols. For example, could "x" represent a specific operation rather than a variable?
This exploration has highlighted the importance of critical thinking, methodical analysis, and the careful application of mathematical principles to decipher complex sequences. The journey to understanding this sequence exemplifies the continuous learning and evolution of mathematical problem-solving.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 3 4x 2 9x 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.