X 3 X 2 X 3
News Co
May 08, 2025 · 6 min read
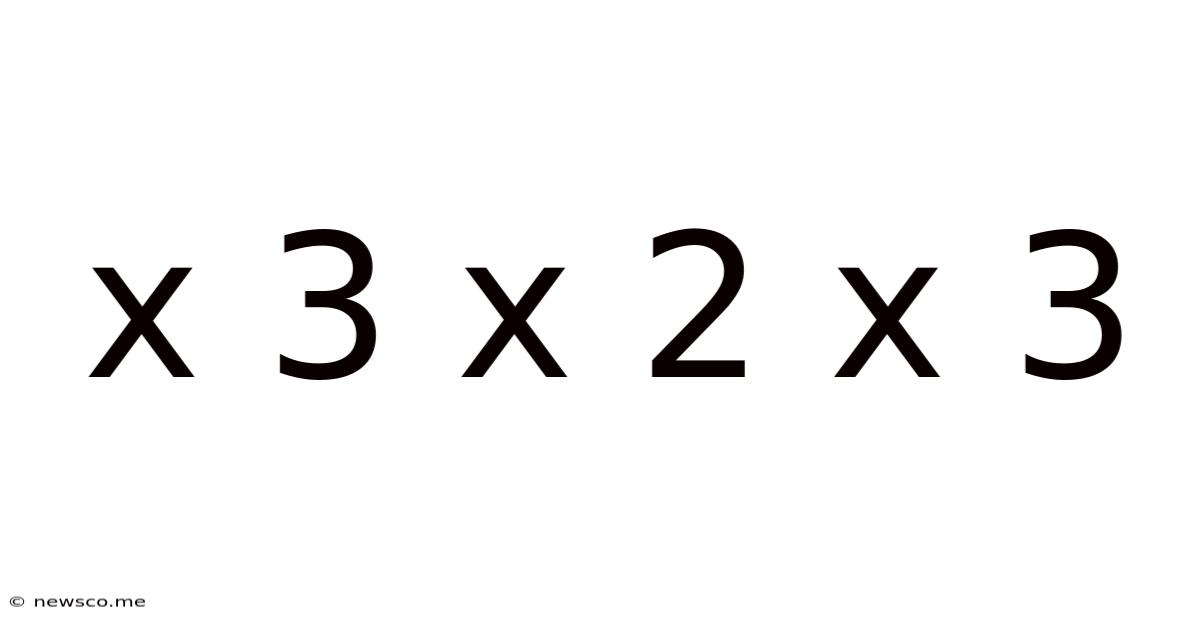
Table of Contents
Decoding the Enigma: A Deep Dive into the Seemingly Simple "x 3 x 2 x 3"
The expression "x 3 x 2 x 3" might appear deceptively simple at first glance. However, a deeper exploration reveals a rich tapestry of mathematical concepts, practical applications, and potential interpretations depending on the context. This article delves into the multifaceted nature of this seemingly basic arithmetic sequence, exploring its significance across various fields, from elementary mathematics to advanced algorithms.
Understanding the Fundamentals: Basic Arithmetic
At its core, "x 3 x 2 x 3" represents a sequence of multiplications. The variable 'x' acts as a placeholder, representing an unknown value. The numbers 3, 2, and 3 are constants, indicating specific multipliers. The order of operations dictates that we perform the multiplication from left to right. Therefore, the expression can be simplified as:
x * 3 * 2 * 3 = 18x
This fundamental simplification highlights the core concept: the expression simplifies to eighteen times the value of 'x'. The simplicity of this initial interpretation should not, however, overshadow the broader implications and varied contexts in which this expression can appear.
Expanding the Scope: Applications Across Disciplines
The seemingly simple "18x" derived from our initial expression has far-reaching applications across numerous disciplines. Let's explore some key areas:
1. Algebra and Equation Solving
In algebra, the expression "x 3 x 2 x 3" forms the basis of many equations. For instance, imagine an equation such as:
18x = 36
Solving this equation involves isolating the variable 'x'. Dividing both sides by 18 gives us:
x = 2
This straightforward example demonstrates how the expression is integral to algebraic problem-solving. The core concept of simplifying the expression is crucial for efficiently solving equations of varying complexity.
2. Geometry and Volume Calculations
Consider a rectangular prism with dimensions:
- Length: x
- Width: 3
- Height: 2 x 3 = 6
The volume of this prism is calculated by multiplying length, width, and height:
Volume = x * 3 * 6 = 18x
This demonstrates that the expression "18x" can represent the volume of a geometric shape, where 'x' represents the length. Variations of this concept extend to other geometric calculations, showcasing the expression's versatility in geometric problem-solving.
3. Physics and Rate Problems
Imagine a car traveling at a speed of 'x' meters per second. If the car maintains this speed for 3 seconds, then slows down to half the speed (x/2) for another 2 seconds, and finally returns to the initial speed for 3 more seconds, the total distance covered can be expressed using our core expression:
Distance = (x * 3) + (x/2 * 2) + (x * 3) = 9x
Although the calculation is not directly represented by 18x, a modification to the initial speed or time parameters could easily lead to an equation directly employing our 18x expression. This example illustrates how the underlying principles of multiplication and variable representation are applicable to complex real-world scenarios.
4. Computer Science and Algorithms
In computer science, the expression "18x" might represent a loop that iterates 18 times, where 'x' could represent the amount of work performed in each iteration. This iterative process is essential in many computational algorithms. Furthermore, understanding the simplification of this expression is fundamental to optimizing algorithms for speed and efficiency.
Furthermore, the concept of repeated multiplication, inherent in "x 3 x 2 x 3," is directly applied in various computer algorithms involving matrix multiplication, which is fundamental to many areas of computing, including machine learning and graphics processing.
5. Finance and Compound Interest
While not directly represented, the concept of repeated multiplication is core to calculating compound interest. The formula involves repeated multiplications, similar to our expression, although typically involving exponents to reflect the compounding effect over time. The core principles of repeated multiplication are therefore directly applicable to understanding the growth of an investment or loan.
Beyond the Basics: Advanced Considerations
The seemingly simple "x 3 x 2 x 3" can be explored further by introducing more complex mathematical concepts:
1. Functions and Mapping
The expression can be viewed as a function, where 'x' is the input and '18x' is the output. This functional approach allows us to explore the relationship between input and output, analyzing its properties and behavior. For instance, we can analyze the function's domain, range, and even its derivative, depending on the context.
2. Calculus and Derivatives
In calculus, we can consider the derivative of the function f(x) = 18x. The derivative, f'(x), which represents the rate of change of the function, is simply 18. This constant derivative implies a consistent rate of change, regardless of the value of 'x'. This analysis reveals more profound insights into the function's behavior and can have implications in optimization problems and other calculus-related applications.
3. Abstract Algebra and Group Theory
At a more abstract level, the expression's multiplicative nature can be examined within the context of group theory. This involves exploring the properties of the multiplicative group of integers modulo n (where 'n' is a specific integer). This is a significant area of abstract algebra, which provides further depth and complexity to understanding the expression's underlying mathematical principles.
Practical Applications and Real-World Scenarios
The understanding of "x 3 x 2 x 3" translates directly to practical real-world applications across a wide range of fields:
- Construction: Calculating material quantities for projects.
- Manufacturing: Determining production rates and output.
- Engineering: Solving equations related to force, stress, and strain.
- Business: Predicting revenue, costs, and profits based on variable factors.
- Data Analysis: Working with spreadsheets and databases to calculate totals and aggregates.
These are just a few examples. The ability to quickly simplify and understand the expression is a foundational skill applicable in a myriad of professional situations.
Conclusion: Unveiling the Power of Simplicity
While seemingly elementary, the expression "x 3 x 2 x 3" reveals a surprising depth of mathematical concepts and practical applications. From basic arithmetic to advanced calculus and abstract algebra, this simple sequence serves as a springboard for understanding more complex mathematical ideas. Moreover, its practical applications across various disciplines underscore the importance of foundational mathematical skills in solving real-world problems. The seemingly simple expression is, in fact, a microcosm of the power and versatility of mathematics itself. By understanding its implications and applications, we can appreciate the beauty and significance of even the simplest mathematical constructs. The ability to simplify and manipulate this expression translates directly into improved problem-solving capabilities and enhances our understanding of the mathematical foundations underlying many complex systems and phenomena. Therefore, a deep understanding of this deceptively simple expression provides a powerful foundation for tackling more challenging mathematical and real-world problems.
Latest Posts
Latest Posts
-
Explain Why This Quadrilateral Is Not A Parallelogram
May 09, 2025
-
What Are The Prime Factorization Of 15
May 09, 2025
-
What Is The Reciprocal Of 9 8
May 09, 2025
-
What Is The Volume Of A Solid Figure
May 09, 2025
-
Corollary To The Isosceles Triangle Theorem
May 09, 2025
Related Post
Thank you for visiting our website which covers about X 3 X 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.