X 3 X 3 X 2
News Co
Mar 27, 2025 · 5 min read
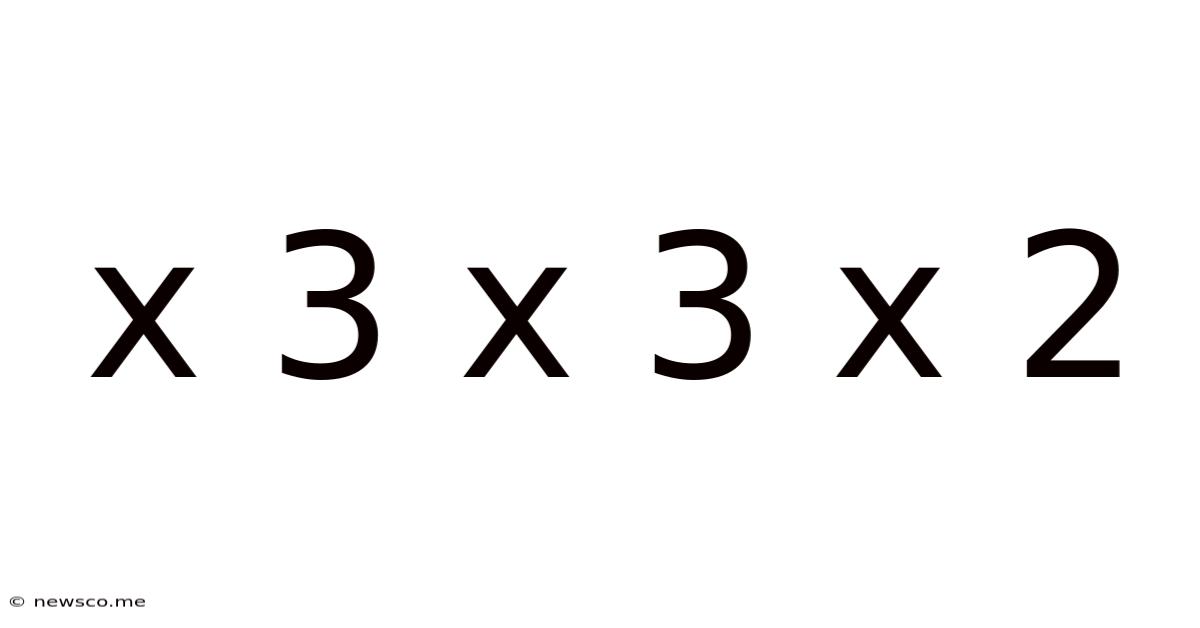
Table of Contents
Decomposing and Exploring 3 x 3 x 3 x 2: A Mathematical Journey
The seemingly simple expression "3 x 3 x 3 x 2" hides a wealth of mathematical concepts and applications. This article will explore this expression in depth, examining its various interpretations, practical uses, and the broader mathematical principles it illustrates. We'll delve into factorization, prime numbers, volume calculations, and even touch upon its relevance in computer science and combinatorics. This comprehensive exploration aims to demonstrate how a seemingly basic calculation can open doors to a deeper understanding of mathematics.
Understanding the Fundamentals: Prime Factorization
At its core, "3 x 3 x 3 x 2" represents a multiplication problem. However, its true power lies in understanding its prime factorization. Prime numbers, which are only divisible by 1 and themselves, are the building blocks of all other numbers. In this case, we have:
- Three factors of 3: This signifies the repeated multiplication of the prime number 3.
- One factor of 2: This is a single instance of the prime number 2.
This prime factorization (2 x 3 x 3 x 3) is unique to the number 54. The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers (disregarding the order of the factors). This fundamental principle is crucial in various areas of mathematics, including cryptography and number theory.
Exploring Factorization Techniques
Finding the prime factorization of a number is a fundamental skill in mathematics. There are several methods, including:
-
Trial Division: This involves systematically dividing the number by each prime number, starting with the smallest (2). This method is straightforward but can be time-consuming for larger numbers.
-
Factor Trees: A visual method using branching to progressively break down the number into its prime factors. This method is particularly helpful for visualizing the factorization process.
-
Algorithm-Based Methods: For very large numbers, sophisticated algorithms like the Pollard rho algorithm or the general number field sieve are employed. These algorithms are computationally efficient for factoring extremely large composite numbers.
Practical Applications: Volume and Dimensions
The expression "3 x 3 x 3 x 2" readily lends itself to geometrical interpretations. Consider a rectangular prism (a box). We can interpret the expression as representing the dimensions of such a prism:
- 3 units x 3 units x 3 units x 2 units: This could represent a box with a base of 3 x 3 units, a height of 3 units and a depth or length of 2 units.
Calculating the volume of this prism is straightforward: Volume = Length x Width x Height. In this case:
- Volume = 3 x 3 x 3 x 2 = 54 cubic units
This shows the direct application of the expression to a real-world problem – calculating the volume of a three-dimensional object.
Beyond Simple Volumes: Applications in Engineering and Design
The ability to calculate volumes precisely is crucial in various engineering disciplines. Think about:
- Civil Engineering: Calculating the volume of concrete needed for a structure.
- Mechanical Engineering: Determining the volume of a component in a machine.
- Architectural Design: Calculating the space within a building.
The fundamental concept of volume calculations using multiplicative expressions like "3 x 3 x 3 x 2" underpins these critical tasks.
Expanding the Scope: Combinatorics and Permutations
While directly related to volume, the expression "3 x 3 x 3 x 2" can also be interpreted within the realm of combinatorics, a branch of mathematics that deals with counting and arranging things.
Imagine you have three different colors of paint (let's say red, blue, and green) and two different brush sizes (small and large). If you wanted to find the number of possible combinations using one color and one brush size, you would use the following calculation:
- Number of color choices (3) x Number of brush size choices (2) = 6 different combinations
This showcases a simpler instance of multiplication leading to combinatoric results. While not directly "3 x 3 x 3 x 2", it demonstrates the broader principle of multiplication in determining the number of possible arrangements or combinations.
Advanced Combinatorial Problems: Expanding the Possibilities
Combinatorial problems can quickly become far more complex. Think about scenarios involving larger sets and multiple choices. The fundamental principle of multiplication, however, remains a core tool for solving these problems, regardless of complexity.
The Expression in Computer Science: Bit Manipulation and Data Structures
In computer science, binary numbers (numbers based on powers of 2) are fundamental. Although "3 x 3 x 3 x 2" doesn't directly translate to a binary operation in a simple manner, the underlying principles of multiplication and factorization are important in several contexts:
-
Bit manipulation: Understanding the binary representation of numbers is crucial for efficient bitwise operations. These operations manipulate individual bits within a number and are used for tasks like data compression and encryption.
-
Data structures: The efficient organization and manipulation of data often require understanding the multiplicative relationships between data elements. For example, calculating the size of an array or determining memory allocation involves multiplicative operations.
Beyond the Calculation: A Springboard to Deeper Mathematical Understanding
The seemingly simple expression "3 x 3 x 3 x 2" serves as an excellent introduction to a range of advanced mathematical concepts. Through its exploration, we've touched upon:
- Prime factorization: A fundamental concept in number theory.
- Volume calculations: An essential part of geometry and engineering.
- Combinatorics: A branch of mathematics dealing with counting and arranging.
- Computer science principles: The role of multiplication in data structures and bit manipulation.
By examining this simple expression, we've seen how interconnected these seemingly disparate areas of mathematics truly are. This demonstrates that even basic mathematical concepts can open doors to a deeper understanding of the mathematical world.
Further Exploration and Challenges: Expanding Your Mathematical Horizons
We encourage further exploration of these concepts. Try to:
- Factorize larger numbers: Challenge yourself with increasingly complex factorization problems.
- Explore different geometric shapes: Calculate the volumes of more complex shapes, utilizing your understanding of multiplicative relationships.
- Investigate advanced combinatorics: Explore problems involving permutations, combinations, and the binomial theorem.
- Learn more about binary numbers and bit manipulation: Delve deeper into the workings of computer science at a fundamental level.
By continually engaging with mathematical concepts and applying them in diverse contexts, you can significantly enhance your mathematical skills and appreciation for the intricate beauty of this discipline. The journey begins with small steps, like understanding the significance of "3 x 3 x 3 x 2," and evolves into a deeper understanding of the mathematical world.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 3 X 3 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.