X Is Greater Than Or Equal To 0
News Co
May 07, 2025 · 7 min read
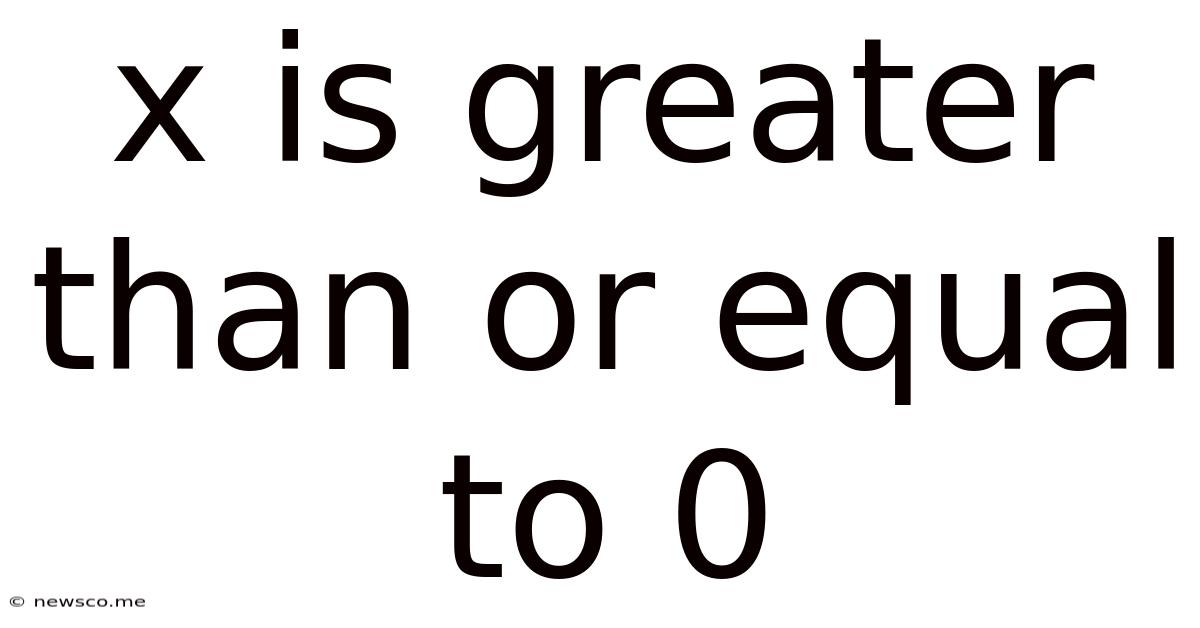
Table of Contents
x ≥ 0: Exploring the Non-Negative Realm in Mathematics
The simple inequality, x ≥ 0, might seem rudimentary at first glance. However, this seemingly straightforward statement underpins a vast array of mathematical concepts and applications, impacting fields from linear programming and probability to computer science and physics. This comprehensive exploration delves into the meaning, implications, and far-reaching consequences of x ≥ 0, demonstrating its significance beyond its initial simplicity.
Understanding the Inequality: x ≥ 0
The inequality x ≥ 0 states that the variable x is greater than or equal to zero. This means x can take on any value on the non-negative portion of the real number line, including zero itself. This seemingly small constraint has profound implications across various mathematical domains. Visualizing this on a number line helps clarify its meaning: a closed circle (or a filled-in dot) at zero indicates that zero is included, and the line extends infinitely to the right, encompassing all positive real numbers.
Key Implications of x ≥ 0
The non-negativity constraint imposed by x ≥ 0 significantly alters the characteristics and potential solutions of mathematical problems. It introduces limitations, but also opens up new avenues of analysis and solution methods specific to this constrained domain.
-
Restricting the Solution Space: This constraint immediately shrinks the potential values x can assume. Instead of ranging across the entire real number line from negative infinity to positive infinity, x is confined to the non-negative half. This restriction simplifies problem-solving in many cases by eliminating irrelevant or impossible solutions.
-
Defining Valid Domains: In many mathematical contexts, particularly those involving functions with square roots, logarithms, or other operations with restricted domains, x ≥ 0 ensures that the operations remain well-defined and avoid mathematical errors such as taking the square root of a negative number or calculating the logarithm of a non-positive number.
-
Enabling Specific Solution Methods: The constraint x ≥ 0 often allows for the application of specialized algorithms and techniques that wouldn't be applicable to the unrestricted real number line. This is particularly relevant in optimization problems, as we will see later.
Applications in Various Mathematical Fields
The impact of the inequality x ≥ 0 extends far beyond its simple definition. Its implications resonate across diverse mathematical branches, shaping their methodologies and solutions.
1. Linear Programming
Linear programming, a crucial technique in operations research and optimization, heavily relies on non-negativity constraints. Many real-world problems, such as resource allocation, production planning, and transportation networks, naturally involve non-negative variables (e.g., you cannot produce a negative number of units). The simplex method, a cornerstone algorithm for solving linear programming problems, often assumes non-negative variables (x ≥ 0, y ≥ 0, etc.) to guarantee the feasibility and optimality of solutions. The constraint significantly simplifies the algorithm's execution and interpretation of results. Without the non-negativity constraint, the problem’s complexity dramatically increases.
2. Probability and Statistics
In probability and statistics, the non-negativity constraint is fundamental. Probabilities, representing the likelihood of events, are always non-negative (0 ≤ P(A) ≤ 1, where P(A) is the probability of event A). Similarly, many statistical measures, like variances and standard deviations, are inherently non-negative due to their definitions involving squared differences. The constraint x ≥ 0 underpins the theoretical foundations of probability distributions, ensuring that the probability mass or density functions remain well-defined and consistent.
3. Calculus and Analysis
The non-negativity constraint plays a critical role in integral calculus and real analysis. In evaluating definite integrals, the limits of integration often define a non-negative interval, ensuring meaningful calculations of areas under curves. Furthermore, concepts like monotonicity and convergence of sequences and series are often studied within the context of non-negative values, simplifying analysis and drawing more straightforward conclusions. For example, proving the convergence of a series of non-negative terms is often easier than proving the convergence of a series with both positive and negative terms.
4. Computer Science and Algorithm Design
The non-negativity constraint appears implicitly and explicitly in various aspects of computer science and algorithm design. Index values in arrays, representing the position of elements, are always non-negative integers (starting from 0 or 1). In graph theory, the weights associated with edges often need to be non-negative, especially in algorithms dealing with shortest paths or minimum spanning trees. The efficiency and correctness of many algorithms depend on these implicit or explicit non-negativity assumptions. Data structures like heaps, designed for efficient sorting and retrieval based on priority, inherently require non-negative keys.
5. Physics and Engineering
Many physical quantities are intrinsically non-negative. For example, mass, energy, temperature (in Kelvin), and length are all non-negative. In classical mechanics, the kinetic energy of a particle is always non-negative, a direct consequence of the definition involving the square of velocity. In quantum mechanics, probabilities of finding a particle in certain states must be non-negative. Engineering applications frequently utilize non-negativity constraints in modelling systems to represent quantities like concentration levels, power output, and material amounts. These constraints ensure physical realism and prevent nonsensical outcomes.
Solving Inequalities Involving x ≥ 0
Solving inequalities that include x ≥ 0 often involves combining the constraint with other inequalities to find the solution set that satisfies all conditions.
Example 1: Simple Combination
Solve the inequality 2x + 3 ≥ 5 and x ≥ 0.
First, solve 2x + 3 ≥ 5: 2x ≥ 2 x ≥ 1
Since x must also satisfy x ≥ 0, the solution set is x ≥ 1. The constraint x ≥ 0 doesn't further restrict the solution because all values greater than or equal to 1 are also greater than or equal to 0.
Example 2: More Complex Scenario
Solve the inequality √(x+2) ≤ 3 and x ≥ 0.
First, we have the constraint x ≥ 0. Next, let's solve √(x+2) ≤ 3: x + 2 ≤ 9 x ≤ 7
Now, we need to find the intersection of the two conditions: x ≥ 0 and x ≤ 7. This means the solution set is 0 ≤ x ≤ 7.
Example 3: Absolute Value Inequality
Solve the inequality |x - 1| ≤ 2 and x ≥ 0.
The inequality |x - 1| ≤ 2 is equivalent to -2 ≤ x - 1 ≤ 2. This simplifies to -1 ≤ x ≤ 3. Combining this with x ≥ 0 gives the solution set 0 ≤ x ≤ 3.
Advanced Concepts and Extensions
The simple inequality x ≥ 0 serves as a foundation for more complex concepts within advanced mathematical fields.
1. Non-Negative Matrices and their Applications
Matrices with all non-negative entries (x<sub>ij</sub> ≥ 0 for all entries) are prevalent in various areas, such as Markov chains, graph theory, and economic modelling. Their properties and associated algorithms (e.g., Perron-Frobenius theorem) are crucial in understanding their behavior and applications.
2. Non-Negative Polynomials and their Roots
Polynomials with only non-negative coefficients have special properties concerning their roots and their behavior on the non-negative real line. Such polynomials appear in numerous applications, including approximation theory and optimization.
3. Cone Programming and its Extensions
Cone programming, a generalization of linear programming, deals with optimization problems over cones (geometric structures with certain properties). The non-negative orthant (the set of all non-negative vectors) is a fundamental example of a cone, and many cone programming problems involve non-negativity constraints. Semidefinite programming, a subclass of cone programming, deals with positive semidefinite matrices, which naturally connects to the non-negativity of eigenvalues.
Conclusion: The Unsung Power of x ≥ 0
The seemingly simple inequality x ≥ 0 is far from trivial. Its presence subtly, yet profoundly, shapes mathematical concepts, problem-solving strategies, and applications across diverse scientific and engineering disciplines. From ensuring the validity of mathematical operations to enabling efficient algorithms and providing the basis for important theoretical results, its significance extends far beyond its initial, straightforward definition. Recognizing its impact provides a deeper understanding of the underlying structure and power of many mathematical frameworks. As we continue to delve into the intricate world of mathematics, the foundational role of this simple inequality remains undeniable.
Latest Posts
Related Post
Thank you for visiting our website which covers about X Is Greater Than Or Equal To 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.