X Less Than Or Equal To
News Co
Mar 17, 2025 · 6 min read
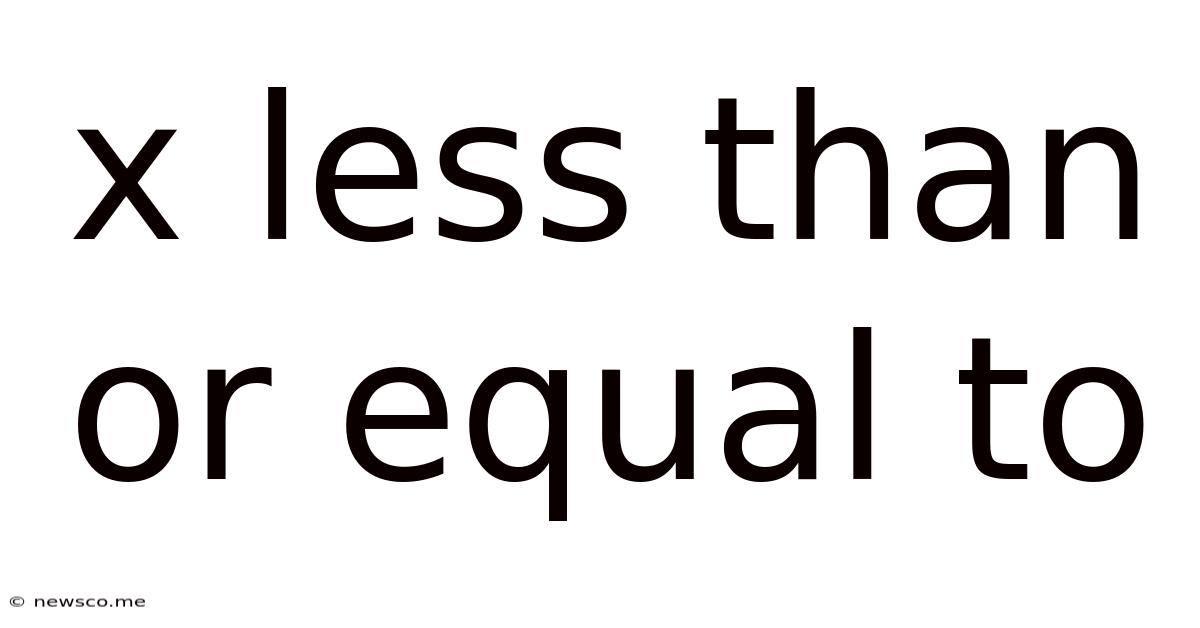
Table of Contents
X Less Than or Equal To: A Comprehensive Guide to Inequalities
The concept of "x less than or equal to" (x ≤) is a fundamental element in mathematics, underpinning a wide range of applications from simple problem-solving to advanced calculus. Understanding this inequality, its graphical representation, and its application in various mathematical contexts is crucial for anyone seeking to master algebraic concepts. This comprehensive guide will delve deep into the intricacies of "x ≤," exploring its meaning, properties, and practical implications.
Understanding the Inequality: x ≤
The symbol "≤" signifies "less than or equal to." This means that the variable 'x' can take on any value that is either strictly less than a given number or exactly equal to that number. Unlike an equation, which asserts equality, an inequality describes a range of possible values.
Example:
If we have the inequality x ≤ 5, this means x can be any number from negative infinity up to and including 5. Thus, x could be 5, 4, 3, 0, -1, -10, or any other number less than or equal to 5.
Graphical Representation of x ≤
Inequalities are often represented graphically on a number line. This visual representation makes it easier to understand the range of values satisfying the inequality.
For "x ≤ 5," the graphical representation would involve:
- Drawing a number line: A horizontal line with numbers marked at regular intervals.
- Locating the critical value: Mark the number 5 on the number line.
- Using a closed circle (or filled-in dot): Since x can be equal to 5, we use a closed circle at 5 to indicate its inclusion in the solution set.
- Shading to the left: Shade the portion of the number line to the left of 5, indicating that all values less than 5 are also part of the solution set.
Solving Inequalities Involving x ≤
Solving inequalities involving "x ≤" follows similar rules to solving equations, with one crucial exception: when multiplying or dividing by a negative number, the inequality sign must be reversed.
Example 1: Simple Inequality
Solve 2x + 3 ≤ 7
- Subtract 3 from both sides: 2x ≤ 4
- Divide both sides by 2: x ≤ 2
The solution is x ≤ 2.
Example 2: Inequality with Negative Multiplication
Solve -3x + 6 ≤ 9
- Subtract 6 from both sides: -3x ≤ 3
- Divide both sides by -3 (and reverse the inequality sign): x ≥ -1
Notice how the inequality sign changed from "≤" to "≥" because we divided by a negative number. The solution is x ≥ -1.
Compound Inequalities involving x ≤
Compound inequalities involve more than one inequality condition. A common type is the "and" compound inequality, which combines two inequalities. For example:
2 ≤ x ≤ 5
This means x must be greater than or equal to 2 and less than or equal to 5. Graphically, this would be represented by a shaded region on the number line between 2 (inclusive) and 5 (inclusive).
Applications of x ≤ in Real-World Scenarios
The "x ≤" inequality has numerous applications in real-world problems:
- Budgeting: If you have a budget of $100 to spend on groceries (x), the inequality x ≤ 100 represents the constraint on your spending.
- Weight limits: If a bridge has a weight limit of 5 tons (x), then x ≤ 5 tons describes the safe weight limit for vehicles crossing the bridge.
- Speed limits: If the speed limit is 65 mph (x), then x ≤ 65 mph represents the legal speed limit.
- Temperature ranges: If a certain plant thrives in temperatures less than or equal to 25°C (x), then x ≤ 25°C represents the optimal temperature range for the plant.
- Manufacturing tolerances: In manufacturing, tolerances specify the acceptable range of variation for a dimension. If the acceptable diameter of a part is less than or equal to 10mm, this can be represented as x ≤ 10mm.
These are just a few examples. The concept of "x ≤" is fundamental to modeling and solving real-world problems involving constraints and limitations.
Solving Inequalities with Absolute Values and x ≤
Absolute value inequalities introduce another layer of complexity. Let's consider inequalities involving the absolute value of x. Recall that the absolute value of a number is its distance from zero. For example, |x| = 3 means x = 3 or x = -3.
Example 1: |x| ≤ 3
This inequality means the distance of x from zero is less than or equal to 3. This translates to:
-3 ≤ x ≤ 3
The solution is the interval [-3, 3].
Example 2: |x + 2| ≤ 5
This is similar to the previous example, but it involves an expression within the absolute value. We solve this by considering two cases:
- Case 1: x + 2 ≥ 0 This implies x ≥ -2. In this case, |x + 2| = x + 2, so we have:
x + 2 ≤ 5 x ≤ 3
Since we assumed x ≥ -2, the solution for this case is -2 ≤ x ≤ 3.
- Case 2: x + 2 < 0 This implies x < -2. In this case, |x + 2| = -(x + 2), so we have:
-(x + 2) ≤ 5 -x - 2 ≤ 5 -x ≤ 7 x ≥ -7
Since we assumed x < -2, the solution for this case is -7 ≤ x < -2.
Combining both cases, the complete solution is -7 ≤ x ≤ 3.
Inequalities in Two Variables and x ≤
Inequalities can also involve two variables, such as x and y. Consider the inequality:
y ≤ x + 2
This represents a half-plane below the line y = x + 2. To graph this, first graph the line y = x + 2. Then, shade the region below the line, because y is less than or equal to x + 2. The line itself is included in the solution set because of the "equal to" part of the inequality.
Solving Systems of Inequalities with x ≤
Often, you'll encounter systems of inequalities, where you need to find the values of x that satisfy multiple inequalities simultaneously. The solution is the intersection of the solution sets of the individual inequalities.
Example:
Find the solution to the system of inequalities:
x ≤ 3 x ≥ -1
The solution to this system is the intersection of x ≤ 3 and x ≥ -1, which is -1 ≤ x ≤ 3. Graphically, it would be the shaded region between -1 and 3 on the number line, inclusive of both endpoints.
Linear Programming and x ≤
Linear programming is an optimization technique used to find the maximum or minimum value of a linear objective function subject to linear constraints, often expressed as inequalities. The "x ≤" inequality plays a critical role in defining the feasible region—the set of all points that satisfy all constraints. The optimal solution is found at one of the vertices (corner points) of the feasible region.
Conclusion: The Importance of x ≤
The seemingly simple inequality "x ≤" forms the backbone of a vast array of mathematical concepts and real-world applications. From basic algebra to advanced optimization techniques, understanding its meaning, graphical representation, and applications is crucial for mastering mathematics and solving practical problems. This guide provides a foundational understanding, enabling you to approach more complex inequalities and related problems with confidence. By mastering the fundamentals of "x ≤," you build a strong mathematical foundation that will serve you well in many future endeavors.
Latest Posts
Latest Posts
-
Find The Point On The Y Axis Which Is Equidistant From
May 09, 2025
-
Is 3 4 Bigger Than 7 8
May 09, 2025
-
Which Of These Is Not A Prime Number
May 09, 2025
-
What Is 30 Percent Off Of 80 Dollars
May 09, 2025
-
Are Alternate Exterior Angles Always Congruent
May 09, 2025
Related Post
Thank you for visiting our website which covers about X Less Than Or Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.