X Square Minus Y Square Is Equal To
News Co
Apr 18, 2025 · 5 min read
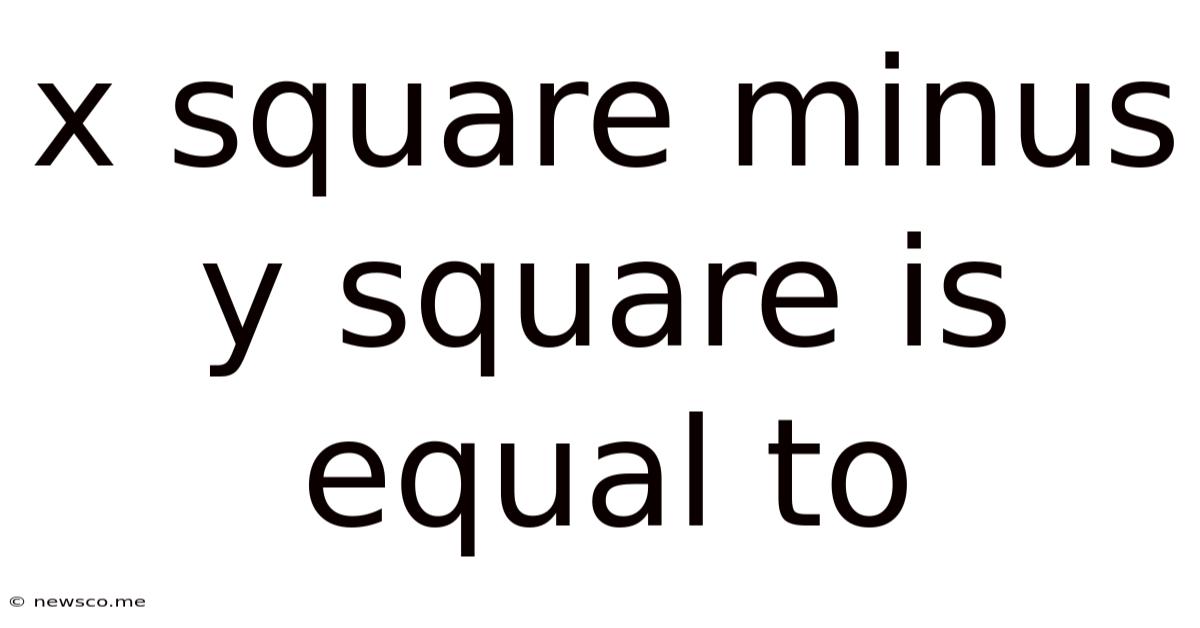
Table of Contents
x² - y² = (x + y)(x - y): A Deep Dive into the Difference of Squares
The equation x² - y² = (x + y)(x - y) represents a fundamental algebraic identity known as the difference of squares. Understanding this identity is crucial for simplifying expressions, solving equations, and tackling more advanced mathematical concepts. This comprehensive guide will explore the difference of squares in detail, covering its derivation, applications, and extensions. We'll delve into its practical uses in various fields, from basic algebra to calculus and beyond.
Understanding the Difference of Squares
The difference of squares states that the difference between two perfect squares (x² and y²) can be factored into the product of their sum (x + y) and their difference (x - y). This seemingly simple identity holds immense power in simplifying complex algebraic expressions.
Let's visualize this through a geometric representation:
Imagine a large square with side length 'x' and a smaller square with side length 'y' cut out from one corner. The area of the large square is x², and the area of the smaller square is y². The remaining area represents the difference of squares, x² - y².
We can rearrange this remaining area into a rectangle. One dimension of this rectangle will be (x + y), and the other will be (x - y). The area of this rectangle is (x + y)(x - y), demonstrating visually that x² - y² = (x + y)(x - y).
Derivation using FOIL
We can also rigorously derive the identity using the FOIL method (First, Outer, Inner, Last) for expanding binomials:
(x + y)(x - y) = x(x) + x(-y) + y(x) + y(-y) = x² - xy + xy - y² = x² - y²
The middle terms, -xy and +xy, cancel each other out, leaving us with the difference of squares, x² - y².
Applications of the Difference of Squares
The difference of squares identity has a wide range of applications across various mathematical domains. Here are some key examples:
1. Simplifying Algebraic Expressions
The identity is invaluable for simplifying complex algebraic expressions. Consider the expression:
4x² - 9y²
This can be factored using the difference of squares as:
(2x)² - (3y)² = (2x + 3y)(2x - 3y)
This simplified form is often easier to manipulate and analyze than the original expression.
2. Solving Quadratic Equations
The difference of squares can simplify the process of solving certain quadratic equations. Consider the equation:
x² - 16 = 0
This can be rewritten as:
x² - 4² = 0
Using the difference of squares, we get:
(x + 4)(x - 4) = 0
This leads to two solutions: x = -4 and x = 4.
3. Calculus and Differentiation
The difference of squares plays a role in various calculus techniques, particularly when dealing with limits and derivatives. For example, when simplifying expressions before applying L'Hôpital's rule, recognizing and applying the difference of squares can simplify calculations significantly.
4. Number Theory
In number theory, the difference of squares is crucial for understanding the properties of integers. It helps in determining whether a number can be factored into specific forms. Fermat's method of factoring relies heavily on this identity.
5. Geometry and Trigonometry
The difference of squares finds applications in geometric problems involving areas and volumes. It's also useful in simplifying trigonometric identities and expressions.
Extending the Difference of Squares
The concept of the difference of squares can be extended to more complex scenarios:
1. Higher Powers
While the basic identity deals with squares, the concept can be generalized to higher powers. For example, the difference of cubes (x³ - y³) can be factored as:
x³ - y³ = (x - y)(x² + xy + y²)
Similarly, there are factorization formulas for higher-order differences of powers.
2. Complex Numbers
The difference of squares holds true even when dealing with complex numbers. For example:
(a + bi)² - (c + di)² = [(a + bi) + (c + di)][(a + bi) - (c + di)]
Where 'i' is the imaginary unit (√-1).
Common Mistakes to Avoid
When applying the difference of squares, several common mistakes should be avoided:
-
Misidentifying Perfect Squares: Ensure that both terms are indeed perfect squares before applying the identity. For instance, x² - 2y isn't a difference of squares because 2y isn't a perfect square.
-
Incorrect Factoring: Pay close attention to the signs. The factored form is (x + y)(x - y), not (x + y)(x + y) or (x - y)(x - y).
-
Overlooking Simplification: After applying the identity, always check if further simplification is possible.
Practical Exercises
To solidify your understanding, try factoring the following expressions using the difference of squares:
- 25x² - 49y²
- 100 - x⁴
- (a + b)² - (c + d)²
- x⁶ - y⁶ (Hint: consider this as a difference of cubes then apply the difference of squares again)
- 16x⁸ - 81y¹⁰
Conclusion
The difference of squares, x² - y² = (x + y)(x - y), is a seemingly simple yet powerful algebraic identity with widespread applications in mathematics and beyond. Mastering this identity is crucial for anyone pursuing a deeper understanding of algebra, calculus, and other related fields. Its versatility extends to simplifying expressions, solving equations, and even exploring more complex mathematical concepts. By understanding its derivation, applications, and potential extensions, you can significantly enhance your mathematical problem-solving skills. Remember to practice regularly to avoid common pitfalls and fully grasp the power of this fundamental algebraic tool. The more you utilize this identity in diverse contexts, the more intuitive and comfortable you'll become with its application. Through consistent practice and application, the difference of squares will transition from a formula to an integral part of your mathematical toolkit.
Latest Posts
Related Post
Thank you for visiting our website which covers about X Square Minus Y Square Is Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.