X Squared Divided By X Squared
News Co
Apr 15, 2025 · 5 min read
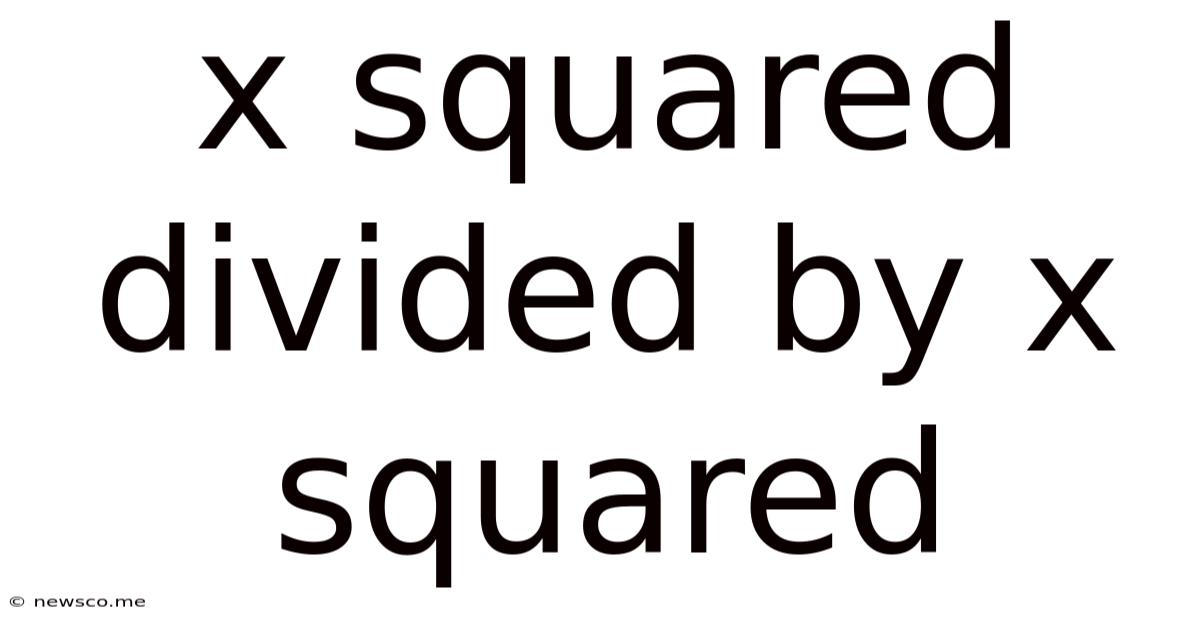
Table of Contents
X Squared Divided by X Squared: A Deep Dive into Mathematical Simplification
The seemingly simple expression "x² / x²" presents a fascinating opportunity to explore fundamental concepts in algebra, particularly concerning simplification, division by zero, and the implications for different mathematical domains. While the immediate answer might appear obvious to many, a closer examination reveals nuances and potential pitfalls that are crucial for a solid understanding of mathematics.
The Obvious Answer and its Limitations
At first glance, the solution to x² / x² is undeniably 1. This is based on the fundamental rule of algebra stating that any number (except zero) divided by itself equals one. This simplification holds true as long as x ≠ 0. This seemingly small caveat is incredibly important, as it highlights the critical issue of division by zero.
The Forbidden Operation: Division by Zero
The concept of dividing by zero is undefined in standard arithmetic. It's not a matter of getting a large or small number; it's a fundamental breach of mathematical rules. Consider the following:
-
Division as the Inverse of Multiplication: Division is defined as the inverse operation of multiplication. If a / b = c, then b * c = a. Now, let's try to apply this to division by zero: If a / 0 = c, then 0 * c = a. This equation only holds true if 'a' is zero. If 'a' is any other number, there's no value of 'c' that satisfies the equation.
-
Limits and Infinity: We might be tempted to say that x² / x² approaches infinity as x approaches zero. While the expression gets arbitrarily large as x gets closer to zero, it doesn't actually equal infinity. Infinity isn't a number in the same way that 1 or -5 is; it's a concept representing unbounded growth.
-
Graphical Representation: Plotting the function y = x²/x² (excluding x=0) would result in a horizontal line at y = 1. However, there would be a "hole" or discontinuity at x = 0, visually representing the undefined nature of the expression at that point.
Therefore, stating that x² / x² = 1 is only accurate under the condition that x is not equal to zero. This conditional statement is crucial for mathematical precision.
Exploring Different Mathematical Contexts
The simplicity of x² / x² belies its multifaceted nature, especially when considering its behaviour within different mathematical frameworks.
Calculus and Limits
Calculus offers a powerful tool for analyzing the behavior of functions near points where they are undefined. Using limits, we can investigate what happens to x² / x² as x approaches 0. The limit of x²/x² as x approaches 0 is indeed 1. This is written as:
lim (x→0) x²/x² = 1
This means that as x gets infinitely close to 0, the value of x²/x² gets infinitely close to 1. However, it's still crucial to remember that the expression is undefined at x = 0. The limit only describes the behavior near that point.
Algebraic Simplification
In the realm of algebraic simplification, the cancellation of common factors is a key technique. We can rewrite x²/x² as (x * x) / (x * x). Since x (assuming x ≠0) is a common factor in both the numerator and the denominator, we can cancel them out, leaving 1. This cancellation process is a cornerstone of algebraic manipulation and provides a concise way to simplify expressions. However, remember that this cancellation only works if the factors being canceled are not equal to zero.
Advanced Algebra and Polynomial Division
When dealing with polynomials, the expression x²/x² can be viewed as polynomial division. Dividing x² by x² results in a quotient of 1 and a remainder of 0. This reinforces the concept of simplification and provides a framework for handling more complex polynomial divisions.
The Importance of Precision and Notation
Mathematical notation is essential for clarity and avoiding ambiguity. Stating simply "x²/x² = 1" is technically inaccurate without the crucial condition that x ≠ 0. The more precise statement would be:
x²/x² = 1, for x ≠ 0
This highlights the importance of precise mathematical language. Omitting the condition can lead to misunderstandings and errors, especially in more advanced mathematical contexts.
Practical Applications and Real-World Scenarios
While this seemingly simple mathematical concept might seem abstract, it has practical applications in various fields. Understanding the conditions under which x²/x² simplifies to 1 is crucial in:
-
Physics: Many physical formulas involve ratios and fractions. Understanding the limitations of simplification prevents errors in calculations and ensures accurate results.
-
Engineering: In engineering calculations, precise mathematical manipulation is critical for safety and reliability. Ignoring the conditions for simplification can lead to significant errors with potentially disastrous consequences.
-
Computer Science: In programming, handling potential division-by-zero errors is essential for creating robust and stable software. Failing to account for this can cause program crashes or unexpected behavior.
-
Economics and Finance: Economic models often involve ratios and fractions. Accurate simplification is vital for making sound financial decisions.
Conclusion: Beyond the Obvious
While the initial response to x² / x² might be a quick "1," a deeper examination reveals a wealth of mathematical concepts and principles. The seemingly straightforward expression highlights the critical importance of understanding division by zero, the power of limits in calculus, the precision of mathematical notation, and the wide-ranging applications of these concepts in various fields. Understanding the nuances surrounding this simple expression strengthens one's foundation in mathematics and improves critical thinking skills crucial for solving more complex problems. It emphasizes that even the simplest expressions can hold hidden complexities and subtle conditions that must be considered for accurate and meaningful interpretations. The journey from the seemingly obvious answer to the deeper understanding is a testament to the beauty and depth of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about X Squared Divided By X Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.