X Squared Times Square Root Of X
News Co
Apr 10, 2025 · 5 min read
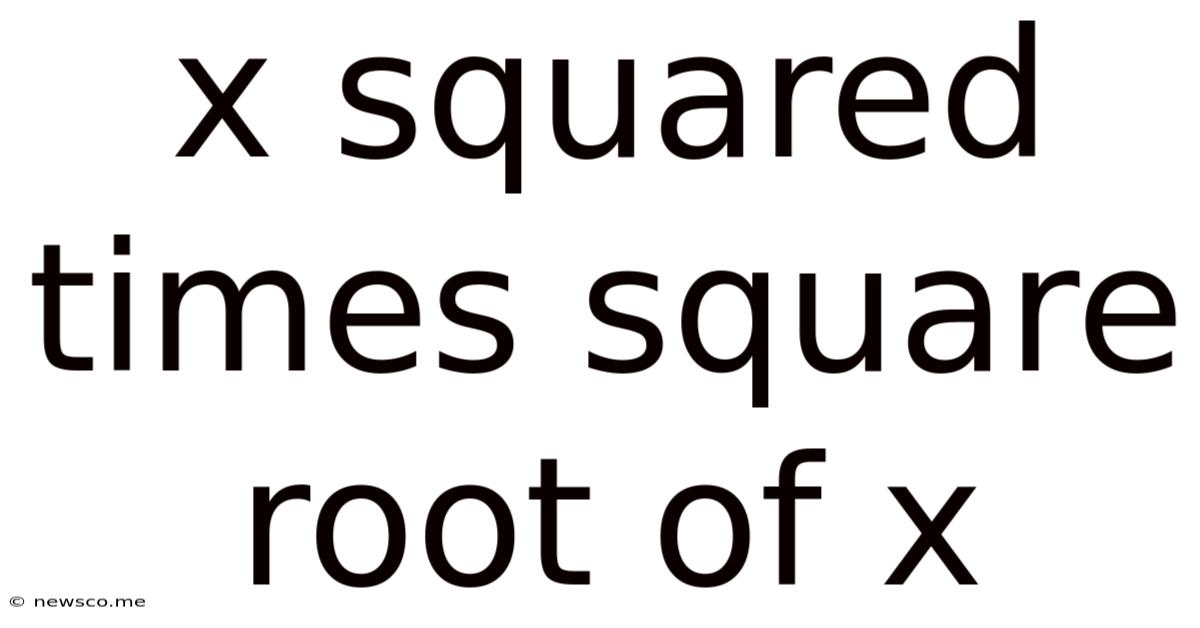
Table of Contents
x²√x: A Deep Dive into Simplifying and Understanding Radical Expressions
Understanding and simplifying radical expressions is a cornerstone of algebra. This article delves into the intricacies of the expression x²√x, exploring its simplification, practical applications, and its relevance within broader mathematical concepts. We'll cover various approaches to simplification, discuss the underlying principles, and even touch upon its representation in calculus.
Understanding the Fundamentals: Exponents and Radicals
Before we dissect x²√x, let's establish a solid foundation in exponents and radicals. Recall that a radical expression, symbolized by the radical symbol √, represents a root (e.g., square root, cube root, etc.). The expression √x is the square root of x, meaning the number that, when multiplied by itself, equals x.
Exponents, on the other hand, represent repeated multiplication. For example, x² means x multiplied by itself (x*x). Understanding the interplay between exponents and radicals is key to simplifying expressions like x²√x.
A critical relationship exists between exponents and radicals: √x can be expressed as x<sup>1/2</sup>. This fractional exponent signifies the square root. Similarly, the cube root of x (∛x) can be written as x<sup>1/3</sup>, and so on. This equivalence is crucial for simplifying complex expressions.
Simplifying x²√x: Combining Exponents
Now, let's tackle the simplification of x²√x. The most straightforward approach leverages the fractional exponent equivalence:
1. Rewrite the Radical as a Fractional Exponent:
We can rewrite √x as x<sup>1/2</sup>. Therefore, x²√x becomes x² * x<sup>1/2</sup>.
2. Apply the Exponent Rule for Multiplication:
When multiplying terms with the same base (in this case, x), we add their exponents. Therefore:
x² * x<sup>1/2</sup> = x<sup>(2 + 1/2)</sup> = x<sup>(5/2)</sup>
3. Final Simplified Form:
Therefore, the simplified form of x²√x is x<sup>5/2</sup>. This representation is more concise and easier to manipulate algebraically.
Alternative Approaches to Simplification
While the fractional exponent method is highly efficient, alternative methods offer further insight into the underlying mathematical principles:
1. Factorization:
We can factor out terms within the radical. Since x² = x * x, we can rewrite the expression as:
√(x² * x)
Since the square root of x² is x, we can simplify to:
x√x
This approach is slightly less concise than the fractional exponent method but highlights the relationship between the squared term and the radical.
2. Visual Representation:
Imagine x²√x as a geometric representation. If we consider x as a length, x² represents the area of a square, and √x a length related to the area. The combined expression then can be viewed as combining these geometric components. While not directly leading to simplification, it provides a more intuitive understanding of the expression's components.
Practical Applications of x<sup>5/2</sup>
The simplified form, x<sup>5/2</sup>, isn't just a theoretical result; it has practical applications across various fields:
1. Calculus:
In calculus, expressions like x<sup>5/2</sup> are common in differentiation and integration problems. The fractional exponent makes it easier to apply power rules for derivatives and integrals. For instance, the derivative of x<sup>5/2</sup> is (5/2)x<sup>3/2</sup>.
2. Physics:
Many physics equations involve fractional exponents. For instance, the power radiated by a black body is proportional to T⁴, where T is temperature. Modifications to this law might involve expressions with fractional exponents, similar to x<sup>5/2</sup>, reflecting complex relationships between physical quantities.
3. Engineering:
Engineering applications, especially those dealing with scaling and geometric relationships, frequently use fractional exponents. The volume of a sphere is proportional to r³. Variations on this concept may introduce fractional exponents, potentially incorporating relationships like x<sup>5/2</sup>.
4. Economics and Finance:
In models describing growth or decay, fractional exponents frequently appear. These models often incorporate time as a variable, where fractional exponents represent non-linear growth patterns.
Expanding the Understanding: Generalization
The techniques used to simplify x²√x are applicable to a broader range of expressions involving exponents and radicals. Consider a more general case:
x<sup>m</sup>√x<sup>n</sup>
Following the same principle, we can rewrite this as:
x<sup>m</sup> * x<sup>n/2</sup> = x<sup>(m + n/2)</sup>
This demonstrates the generality of the approach. The specific values of 'm' and 'n' will determine the final simplified form, but the methodology remains consistent.
Potential Pitfalls and Considerations
While simplifying these expressions is relatively straightforward, certain considerations can prevent errors:
1. Restrictions on the Variable:
Remember that the square root of a negative number is undefined within the real number system. Therefore, if x is a negative number, the expression x²√x would be undefined in the context of real numbers (although it may have a solution in the complex number system).
2. Simplification vs. Solution:
Simplification aims to express an equation in a more concise or manageable form. It's crucial not to confuse simplification with solving an equation. Simplification alters the form of the expression without changing its value; solving an equation seeks to determine the value of the variable that satisfies the equation.
Conclusion: Mastering Radical Expressions
Mastering the simplification of expressions like x²√x is essential for success in algebra and its various applications. By understanding the interplay between exponents and radicals and applying the rules of exponents, we can efficiently simplify complex expressions, ultimately making them easier to work with in more advanced mathematical contexts. The approaches discussed – from fractional exponents to factorization and visual representations – provide a multi-faceted understanding of these fundamental algebraic concepts. Remember the importance of considering the domain of the variables to avoid errors and appreciate the practical relevance of these techniques across diverse fields. Continuing to practice and explore these concepts will undoubtedly strengthen your mathematical abilities and problem-solving skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about X Squared Times Square Root Of X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.