Y Mx B Solve For B
News Co
Apr 12, 2025 · 6 min read
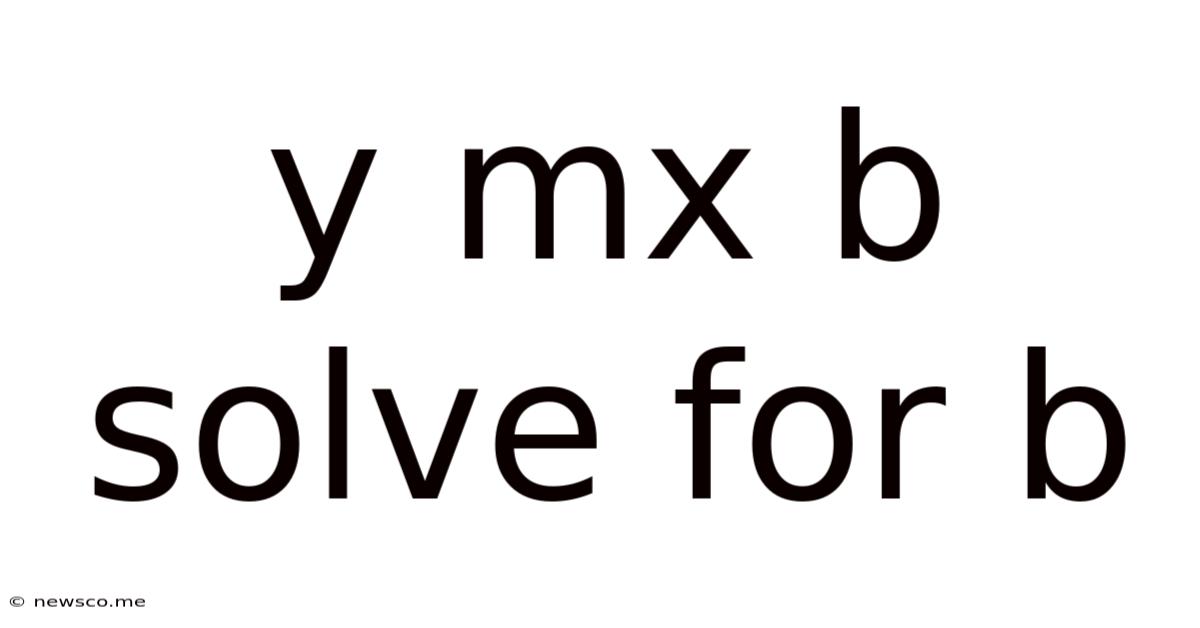
Table of Contents
Solving for b: A Deep Dive into the Equation y = mx + b
The equation y = mx + b represents a fundamental concept in algebra and is the slope-intercept form of a linear equation. Understanding this equation and how to manipulate it is crucial for various mathematical applications, from graphing lines to solving complex real-world problems. This comprehensive guide delves into the intricacies of solving for 'b' in the equation y = mx + b, providing step-by-step instructions, practical examples, and insightful explanations to solidify your understanding.
Understanding the Components of y = mx + b
Before we tackle solving for 'b', let's review what each component of the equation represents:
-
y: Represents the dependent variable. Its value depends on the value of x. Think of 'y' as the output or result.
-
x: Represents the independent variable. You can choose any value for 'x', and the equation will calculate the corresponding value of 'y'. 'x' is the input.
-
m: Represents the slope of the line. The slope indicates the steepness and direction of the line. A positive slope indicates an upward trend, while a negative slope indicates a downward trend. The slope is calculated as the change in 'y' divided by the change in 'x' (rise over run).
-
b: Represents the y-intercept. The y-intercept is the point where the line crosses the y-axis (where x = 0). It's the value of 'y' when x is zero.
Step-by-Step Guide to Solving for b
The process of solving for 'b' in the equation y = mx + b is relatively straightforward. It involves isolating 'b' on one side of the equation using algebraic manipulations. Here's a step-by-step guide:
1. Identify the known values:
First, you need to identify the values of y, m, and x. These values will be given to you in a problem or derived from a graph. Without these values, you cannot solve for 'b'.
2. Substitute the known values into the equation:
Substitute the known values of y, m, and x into the equation y = mx + b. Make sure to replace the variables with their corresponding numerical values.
3. Isolate 'b':
To isolate 'b', you need to perform the following algebraic operations:
-
Subtract mx from both sides of the equation: This step removes the 'mx' term from the right-hand side, leaving only 'b'. The equation will now look like this:
y - mx = b -
Rearrange the equation (optional): While not strictly necessary, it's common practice to rearrange the equation to have 'b' on the left-hand side. This gives you:
b = y - mx
4. Calculate the value of b:
Finally, perform the arithmetic calculations to determine the numerical value of 'b'. This involves subtracting the product of 'm' and 'x' from 'y'.
Example Problems: Solving for b
Let's work through a few examples to illustrate the process:
Example 1:
Given: y = 10, m = 2, x = 3
- Substitute: 10 = 2(3) + b
- Isolate b: 10 - 6 = b
- Calculate b: b = 4
Therefore, the y-intercept (b) is 4.
Example 2:
Given: y = -5, m = -1, x = 2
- Substitute: -5 = -1(2) + b
- Isolate b: -5 + 2 = b
- Calculate b: b = -3
Therefore, the y-intercept (b) is -3.
Example 3: A more complex scenario
Let's say you are given two points on a line: (2, 5) and (4, 9). First, you need to calculate the slope (m) using the formula: m = (y2 - y1) / (x2 - x1).
-
Calculate the slope (m): m = (9 - 5) / (4 - 2) = 4 / 2 = 2
-
Substitute one point into the equation: Let's use (2, 5). Substitute y = 5, m = 2, and x = 2 into
y = mx + b: 5 = 2(2) + b -
Isolate b: 5 - 4 = b
-
Calculate b: b = 1
Therefore, the y-intercept (b) is 1.
Practical Applications of Solving for b
Solving for 'b' is not just a theoretical exercise; it has various practical applications across different fields:
-
Graphing Linear Equations: The y-intercept ('b') is a crucial point for graphing a linear equation. Knowing 'b' allows you to plot one point on the graph immediately, making it easier to draw the entire line.
-
Data Analysis: In data analysis, the y-intercept can represent a baseline value or initial condition. For example, in a sales trend analysis, 'b' could represent the initial sales before a marketing campaign.
-
Predictive Modeling: Linear equations are used for predictive modeling in various fields, such as finance, economics, and engineering. The y-intercept provides valuable insights into the initial state or expected value before the effect of other variables.
-
Physics and Engineering: Many physical phenomena can be modeled using linear equations. Solving for 'b' provides valuable insights into the initial conditions or constant parameters within the system.
-
Computer Programming: Linear equations and their manipulation are frequently encountered in computer programming, particularly in graphics programming and game development. Understanding how to solve for 'b' is essential for programmers who are working on algorithms involving lines and coordinate systems.
Advanced Concepts and Extensions
While the basic process of solving for 'b' is relatively simple, there are more complex scenarios to consider:
-
Systems of Equations: Sometimes you might need to solve for 'b' in a system of linear equations. This typically involves using techniques like substitution or elimination to solve for all the unknowns simultaneously.
-
Nonlinear Equations: The concept of a y-intercept extends to some nonlinear equations, although the calculation might be more complex.
-
Multivariable Equations: In multivariable calculus, linear equations can involve multiple independent variables. The concept of a y-intercept is extended to hyperplanes, and solving for the constants requires more advanced techniques.
Troubleshooting Common Mistakes
Here are some common mistakes to avoid when solving for 'b':
-
Incorrect substitution: Double-check your substitutions to ensure you're using the correct values for y, m, and x.
-
Algebraic errors: Carefully review your algebraic manipulations to avoid errors in addition, subtraction, multiplication, and division.
-
Order of operations: Remember to follow the order of operations (PEMDAS/BODMAS) when performing calculations.
-
Misinterpreting the results: Make sure you correctly interpret the value of 'b' in the context of the problem.
Conclusion: Mastering the Art of Solving for b
Solving for 'b' in the equation y = mx + b is a fundamental skill in algebra that opens doors to a wide range of applications. By understanding the components of the equation, following the step-by-step process, and practicing with examples, you can confidently solve for 'b' and apply this knowledge to various mathematical and real-world problems. Remember to practice regularly and review the common mistakes to further improve your understanding and accuracy. With consistent effort, you’ll master this valuable skill and enhance your overall mathematical proficiency.
Latest Posts
Related Post
Thank you for visiting our website which covers about Y Mx B Solve For B . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.