Y Varies Directly As X And Inversely As Z
News Co
May 07, 2025 · 5 min read
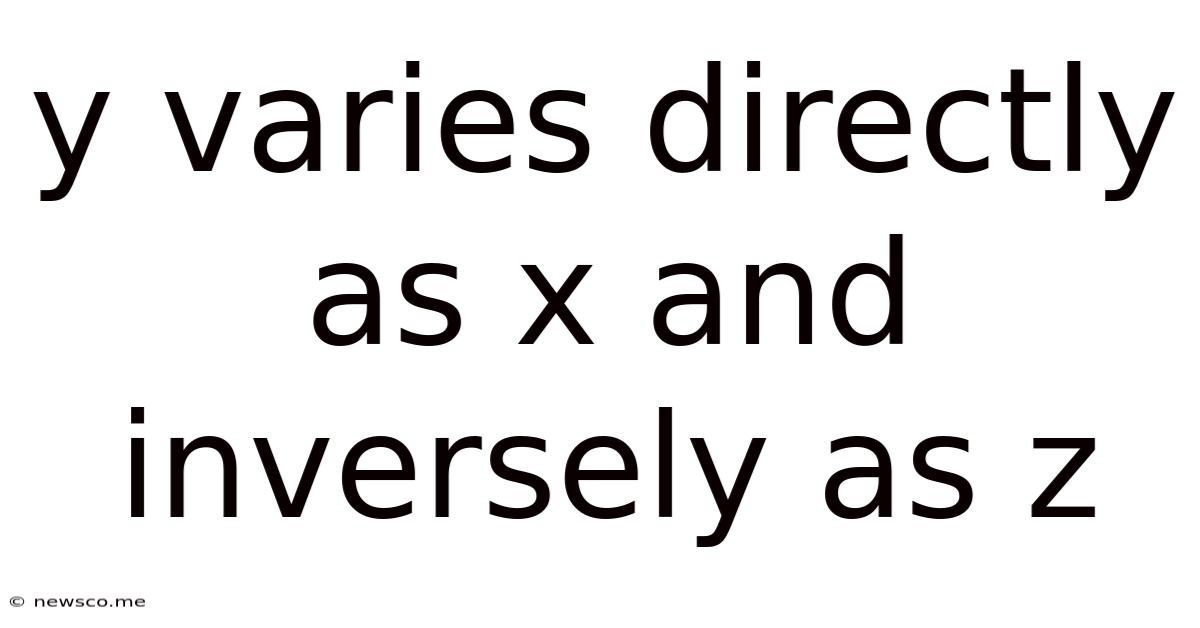
Table of Contents
Y Varies Directly as X and Inversely as Z: A Comprehensive Guide
Understanding the relationship between variables is fundamental in mathematics and numerous real-world applications. This article delves deep into the concept of "y varies directly as x and inversely as z," exploring its mathematical representation, practical applications, and how to solve problems involving this type of variation. We'll cover everything from the basic definition to advanced problem-solving techniques, ensuring a comprehensive understanding for students and professionals alike.
Understanding Direct and Inverse Variation
Before diving into the combined variation, let's solidify our understanding of direct and inverse variations individually.
Direct Variation
In direct variation, two variables are directly proportional. This means that as one variable increases, the other variable increases proportionally, and vice versa. The relationship can be expressed mathematically as:
y = kx
where:
- y and x are the variables.
- k is the constant of proportionality (a constant value).
This equation indicates that y is directly proportional to x; if x doubles, y doubles; if x triples, y triples, and so on. The graph of a direct variation is a straight line passing through the origin (0,0).
Inverse Variation
Inverse variation, on the other hand, describes an inversely proportional relationship. As one variable increases, the other variable decreases proportionally, and vice versa. The mathematical representation is:
y = k/x
where:
- y and x are the variables.
- k is the constant of proportionality.
In this case, if x doubles, y is halved; if x triples, y is reduced to one-third, and so on. The graph of an inverse variation is a hyperbola.
Combining Direct and Inverse Variation: y Varies Directly as X and Inversely as Z
Now, let's explore the scenario where a variable (y) varies directly with one variable (x) and inversely with another variable (z). This combined variation can be expressed as:
y = kx/z
where:
- y is the dependent variable.
- x and z are the independent variables.
- k is the constant of proportionality.
This equation signifies that y increases proportionally with x but decreases proportionally with z. If x doubles, y doubles; if z doubles, y is halved. The interplay between direct and inverse proportionality makes this type of problem more complex but equally fascinating.
Solving Problems Involving Combined Variation
Let's illustrate how to solve problems involving combined variation with examples. The key is to find the constant of proportionality (k) using given information and then utilize this constant to solve for unknown variables.
Example 1: Finding the Constant of Proportionality
The variable y varies directly as x and inversely as z. If y = 6 when x = 2 and z = 3, find the constant of proportionality k.
Solution:
- We start with the formula:
y = kx/z - Substitute the given values:
6 = k(2)/3 - Solve for k:
k = (6 * 3) / 2 = 9
Therefore, the constant of proportionality is 9. The complete equation describing the variation is: y = 9x/z
Example 2: Solving for an Unknown Variable
Using the equation from Example 1 (y = 9x/z), find the value of y when x = 4 and z = 6.
Solution:
- Substitute the given values into the equation:
y = 9(4)/6 - Solve for y:
y = 36/6 = 6
Therefore, when x = 4 and z = 6, y = 6.
Example 3: A More Complex Scenario
The volume (V) of a gas varies directly as its temperature (T) and inversely as its pressure (P). If V = 20 liters when T = 300 Kelvin and P = 2 atmospheres, find the volume when T = 350 Kelvin and P = 2.5 atmospheres.
Solution:
- Establish the equation:
V = kT/P - Find k using the initial values:
20 = k(300)/2=>k = (20 * 2) / 300 = 2/15 - The complete equation is:
V = (2/15)T/P - Substitute the new values:
V = (2/15)(350)/2.5 - Solve for V:
V = (700/15) / 2.5 = 18.67liters (approximately).
This problem demonstrates the practical application of combined variation in physics, specifically in the Ideal Gas Law.
Real-World Applications of Combined Variation
Combined variation isn't just a mathematical concept; it has numerous real-world applications across various fields:
-
Physics: The Ideal Gas Law (as shown in Example 3), relating pressure, volume, and temperature of a gas, is a prime example. Other applications include gravitational force, electrical force, and magnetic fields.
-
Engineering: Designing structures and systems often involves considerations of combined variations. For instance, the strength of a beam might vary directly with its width and inversely with its length.
-
Economics: Demand for a product may vary directly with consumer income and inversely with its price.
-
Chemistry: Chemical reactions often involve variables that exhibit combined variation. The rate of a reaction might vary directly with the concentration of reactants and inversely with the activation energy.
Advanced Problem-Solving Techniques
For more complex problems, techniques like dimensional analysis and setting up proportions can prove helpful. Dimensional analysis ensures the units are consistent throughout the calculation, while setting up proportions provides a structured approach to solving for unknown variables.
Conclusion
Understanding combined variation, specifically where 'y varies directly as x and inversely as z,' is crucial for solving a wide array of mathematical and real-world problems. By mastering the fundamental concepts and applying the problem-solving techniques discussed, you can confidently tackle complex scenarios across various disciplines. Remember to always identify the constant of proportionality and use it consistently throughout your calculations. The practical applications of this concept extend far beyond the classroom, demonstrating its importance in understanding the relationships between variables in our world. Continued practice and exploration of diverse examples will strengthen your understanding and problem-solving skills.
Latest Posts
Related Post
Thank you for visiting our website which covers about Y Varies Directly As X And Inversely As Z . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.