1/2 Divided By 1/6 In Fraction Form
News Co
May 07, 2025 · 5 min read
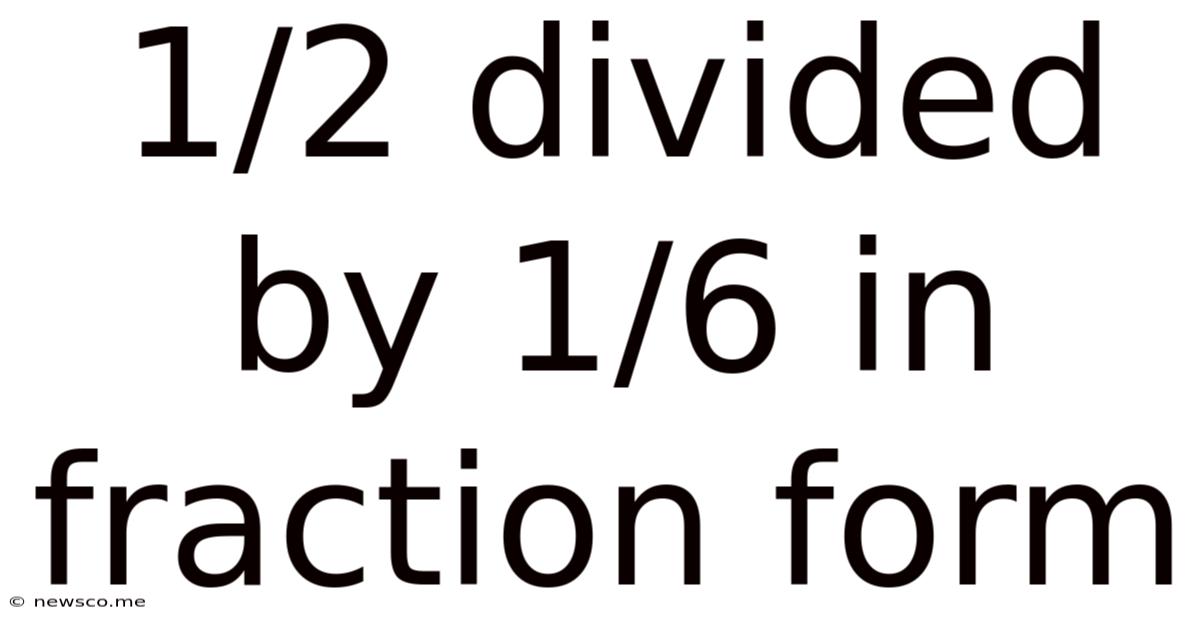
Table of Contents
1/2 Divided by 1/6 in Fraction Form: A Comprehensive Guide
Understanding fraction division can be tricky, but mastering it opens up a world of mathematical possibilities. This comprehensive guide will walk you through the process of dividing 1/2 by 1/6, explaining the underlying principles and providing practical examples to solidify your understanding. We'll explore various methods, delve into the reasoning behind each step, and offer tips to tackle similar fraction division problems with confidence.
Understanding Fraction Division
Before we tackle the specific problem of 1/2 ÷ 1/6, let's establish a solid foundation in fraction division. The core concept revolves around the idea of finding out how many times one fraction fits into another. Unlike multiplication, where we find the combined size, division focuses on finding how many times one quantity is contained within another.
The "Keep, Change, Flip" Method
One of the most common and easiest methods for dividing fractions is the "Keep, Change, Flip" method (also known as the reciprocal method). This method simplifies the process significantly:
- Keep: Keep the first fraction exactly as it is.
- Change: Change the division sign (÷) to a multiplication sign (×).
- Flip: Flip the second fraction (find its reciprocal). The reciprocal of a fraction is simply the fraction turned upside down; the numerator becomes the denominator, and vice-versa.
Let's illustrate this with a simple example: 1/3 ÷ 1/2.
Following the "Keep, Change, Flip" method:
- Keep: 1/3
- Change: ÷ becomes ×
- Flip: 1/2 becomes 2/1 (or simply 2)
This transforms the division problem into a multiplication problem: 1/3 × 2/1 = 2/3.
Solving 1/2 Divided by 1/6
Now, let's apply this method to our specific problem: 1/2 ÷ 1/6.
- Keep: 1/2
- Change: ÷ becomes ×
- Flip: 1/6 becomes 6/1 (or simply 6)
This gives us the multiplication problem: 1/2 × 6/1.
To multiply fractions, we multiply the numerators together and the denominators together:
(1 × 6) / (2 × 1) = 6/2
Finally, we simplify the resulting fraction by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 2:
6/2 = 3
Therefore, 1/2 ÷ 1/6 = 3.
This means that 1/6 fits into 1/2 three times.
Alternative Methods and Deeper Understanding
While the "Keep, Change, Flip" method is efficient, understanding the underlying principles can provide a more robust grasp of fraction division.
Visual Representation
Imagine you have a pizza cut into two equal halves (representing 1/2). Now, imagine each half is further divided into three smaller slices (creating six slices in total). Each of these smaller slices represents 1/6 of the whole pizza. How many of these 1/6 slices are contained within one of the original halves (1/2)?
You'll see that there are three 1/6 slices within one 1/2 slice. This visually confirms our answer of 3.
Common Denominator Method
Another approach involves finding a common denominator for both fractions. While less direct than the "Keep, Change, Flip" method, it reinforces the concept of equivalent fractions.
To divide 1/2 by 1/6 using this method, we first find a common denominator for 2 and 6, which is 6.
We convert both fractions to have a denominator of 6:
1/2 = 3/6 (multiply numerator and denominator by 3) 1/6 = 1/6
Now, we can rewrite the division problem as:
(3/6) ÷ (1/6)
When the denominators are the same, we can simply divide the numerators:
3 ÷ 1 = 3
This method, though slightly longer, illustrates the equivalence of fractions and provides an alternative perspective on fraction division.
Practical Applications and Real-World Examples
Understanding fraction division is not just an academic exercise; it's a crucial skill with many practical applications in everyday life:
- Cooking: Recipes often require dividing ingredients. If a recipe calls for 1/2 cup of flour and you only want to make 1/6 of the recipe, you'd need to calculate 1/2 ÷ 6 = 1/12 cup of flour.
- Sewing: Calculating fabric requirements for smaller projects often involves dividing fractions.
- Construction: Precise measurements in construction frequently utilize fractions, and understanding division is essential for accurate calculations.
- Data Analysis: Many data analysis tasks involve dealing with fractions and percentages, requiring proficiency in fraction division.
Tackling More Complex Fraction Division Problems
The principles we've covered extend to more complex fraction division problems. Here are some tips for tackling these:
- Simplify before you begin: If either fraction can be simplified, do so before applying the "Keep, Change, Flip" method. This will make the multiplication step easier.
- Mixed numbers: If you encounter mixed numbers (e.g., 1 1/2), convert them to improper fractions before performing the division. An improper fraction has a larger numerator than denominator.
- Multiple fractions: If you are dividing by more than one fraction, perform the divisions sequentially, one at a time.
Conclusion: Mastering Fraction Division
Mastering fraction division is a fundamental building block in mathematics and has wide-ranging practical applications. The "Keep, Change, Flip" method provides an efficient and easy-to-remember approach, while understanding alternative methods like the common denominator method strengthens your conceptual understanding. By practicing regularly and applying these principles, you'll build confidence and competence in tackling even the most complex fraction division problems. Remember to always simplify your answers to their lowest terms to ensure accuracy and clarity. With consistent practice and a clear understanding of the underlying concepts, you'll become proficient in handling fraction division, paving the way for further mathematical exploration and success in various fields.
Latest Posts
Latest Posts
-
Each Axis On A Graph Should Be
May 07, 2025
-
How Many 5 8 Are In 1
May 07, 2025
-
Converting Units Of Measurement Worksheet Pdf
May 07, 2025
-
If What Is The Value Of X
May 07, 2025
-
How To Write 450 Dollars On A Check
May 07, 2025
Related Post
Thank you for visiting our website which covers about 1/2 Divided By 1/6 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.