1 2 Divided By 6 In Fraction Form
News Co
May 07, 2025 · 5 min read
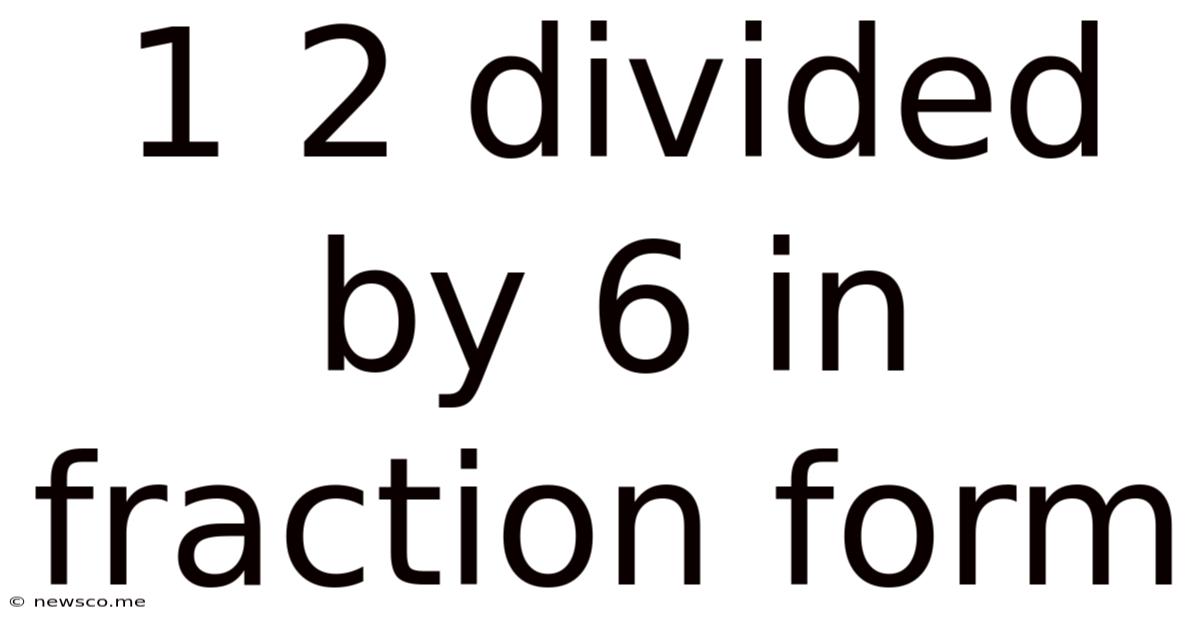
Table of Contents
1/2 Divided by 6: A Deep Dive into Fraction Division
This article explores the seemingly simple mathematical problem of dividing one-half (1/2) by 6, offering a comprehensive explanation suitable for various levels of mathematical understanding. We will unpack the process, discuss the underlying principles of fraction division, and explore related concepts to build a solid foundation in this area of mathematics. We'll also touch upon practical applications and delve into the reasons behind the specific steps involved.
Understanding Fraction Division: The "Invert and Multiply" Rule
The core concept behind dividing fractions involves a crucial rule: invert the second fraction (the divisor) and multiply. This seemingly simple rule underpins a deeper mathematical principle, but for now, let's focus on its practical application.
When we divide 1/2 by 6, we can rewrite 6 as a fraction: 6/1. Our problem then becomes:
(1/2) ÷ (6/1)
Applying the "invert and multiply" rule, we flip the second fraction (6/1 becomes 1/6) and change the division sign to a multiplication sign:
(1/2) x (1/6)
Now, multiplying fractions is straightforward: we multiply the numerators (top numbers) together and the denominators (bottom numbers) together:
(1 x 1) / (2 x 6) = 1/12
Therefore, 1/2 divided by 6 is equal to 1/12.
Visualizing Fraction Division: A Practical Approach
While the "invert and multiply" rule provides a quick and efficient method, visualizing the problem can enhance understanding. Imagine you have half a pizza (1/2). You want to divide this half-pizza into 6 equal slices. Each of these slices represents 1/12th of the original whole pizza.
This visual representation helps solidify the concept that dividing a fraction by a whole number results in a smaller fraction. The denominator increases, reflecting the increased number of parts the original fraction is divided into.
Delving Deeper: The Mathematical Rationale
The "invert and multiply" rule isn't arbitrary; it's grounded in the principles of reciprocal numbers and multiplicative inverses. The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 6 is 1/6.
Dividing by a number is the same as multiplying by its reciprocal. This is why we invert the second fraction and multiply. Mathematically, this is represented as follows:
(a/b) ÷ (c/d) = (a/b) x (d/c)
Where 'a', 'b', 'c', and 'd' are numbers, and 'b' and 'c' are not equal to zero (as division by zero is undefined).
This principle applies regardless of the complexity of the fractions involved. The ability to convert division into multiplication simplifies calculations considerably.
Practical Applications of Fraction Division
Fraction division is not confined to theoretical exercises; it finds applications in various real-world scenarios:
-
Cooking and Baking: Recipes often require adjustments based on the number of servings. If a recipe calls for 1/2 cup of flour and you want to make only 1/6 of the recipe, you'd need to divide 1/2 by 6 to determine the amount of flour needed (1/12 cup).
-
Construction and Engineering: Precise measurements are crucial in these fields. Dividing fractions is essential for calculating material quantities or adjusting plans based on scaled drawings.
-
Finance and Budgeting: Dividing a budget or a share of profit between multiple individuals often involves fraction division.
-
Science and Research: Data analysis in scientific fields frequently involves dealing with fractions and proportions, requiring calculations like dividing one fraction by another.
Beyond the Basics: Working with More Complex Fractions
While 1/2 divided by 6 is a relatively straightforward problem, the principles discussed extend to more complex scenarios. Consider dividing a fraction by a mixed number or another fraction. The core concept remains the same:
-
Convert mixed numbers to improper fractions: A mixed number (e.g., 1 1/2) needs to be converted into an improper fraction (e.g., 3/2) before applying the "invert and multiply" rule.
-
Simplify before multiplying: After inverting the second fraction and changing the operation to multiplication, it is often beneficial to simplify the fractions before performing the multiplication. This can reduce the size of the numbers and make the calculation easier. For example, if you have (2/6) x (3/4), you can simplify 2/6 to 1/3 before multiplying, making the calculation less cumbersome.
-
Reduce to the lowest terms: Once the multiplication is completed, reduce the resulting fraction to its lowest terms (simplest form) by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
Troubleshooting Common Mistakes
Several common mistakes can occur when dividing fractions. Understanding these pitfalls can help avoid errors:
-
Forgetting to invert: This is the most frequent error. Remember, you must invert (reciprocate) the second fraction before multiplying.
-
Incorrect simplification: Failure to simplify fractions before or after multiplication can lead to cumbersome calculations and incorrect answers.
-
Mixing up multiplication and division: Carefully review the operation to ensure you are applying the "invert and multiply" rule correctly.
Conclusion: Mastering Fraction Division
Understanding fraction division is fundamental to a strong mathematical foundation. The "invert and multiply" rule, though simple in its application, stems from deeper mathematical principles. By grasping these principles, visualizing the problem, and practicing regularly, you can confidently tackle more complex fraction division problems and apply this skill to various real-world situations. Remember to practice regularly to solidify your understanding and build confidence in your mathematical abilities. The more you work with fractions, the more intuitive the process will become. This article serves as a stepping stone to mastering this essential mathematical skill, empowering you to approach more complex problems with ease and confidence. Through practice and a thorough understanding of the underlying principles, you will become proficient in fraction division and its numerous applications.
Latest Posts
Latest Posts
-
The Ratios Of The Variables Are Not Equivalent Equal
May 08, 2025
-
List All The Factors Of 6
May 08, 2025
-
Find Area Of A Parallelogram With Vertices
May 08, 2025
-
1 3 4 2 1 2
May 08, 2025
-
How To Divide Decimals With Fractions
May 08, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Divided By 6 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.