11 Over 5 As A Mixed Number
News Co
May 08, 2025 · 5 min read
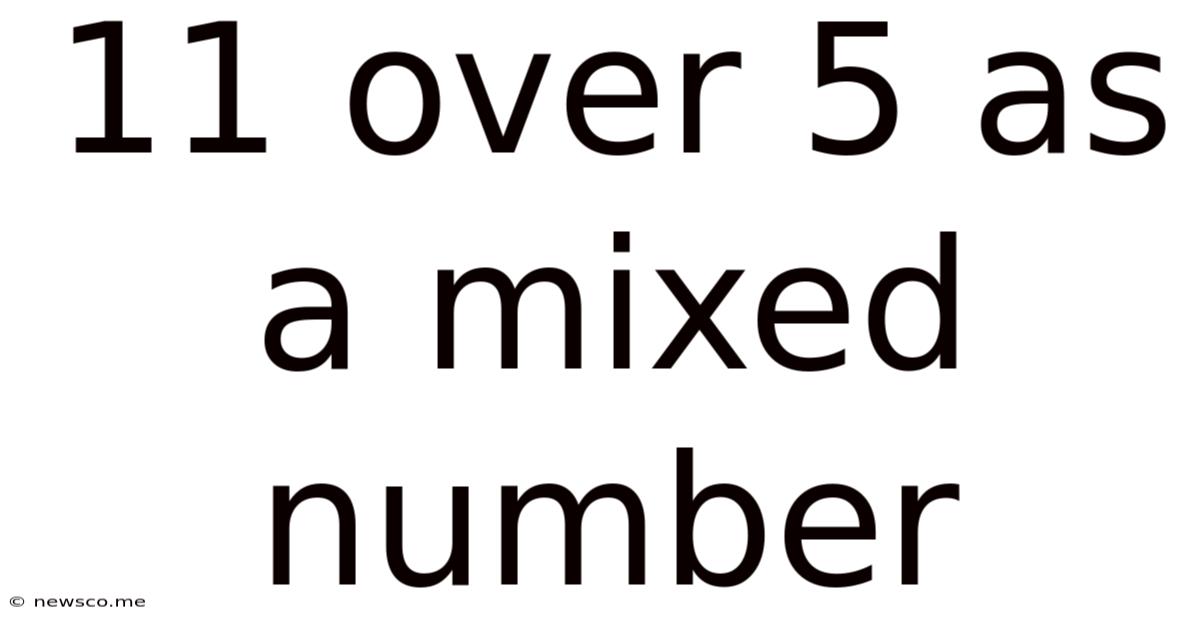
Table of Contents
11 Over 5 as a Mixed Number: A Comprehensive Guide
Converting improper fractions to mixed numbers is a fundamental skill in mathematics. Understanding this process is crucial for various applications, from basic arithmetic to more advanced calculations in algebra and calculus. This comprehensive guide will delve into the conversion of the improper fraction 11/5 into a mixed number, explaining the process step-by-step and providing numerous examples to solidify your understanding. We'll also explore the practical applications and significance of this conversion.
Understanding Improper Fractions and Mixed Numbers
Before we tackle the conversion of 11/5, let's clarify the definitions:
-
Improper Fraction: An improper fraction is a fraction where the numerator (the top number) is greater than or equal to the denominator (the bottom number). Examples include 7/4, 11/5, and 9/9.
-
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction is where the numerator is smaller than the denominator. Examples include 1 ¾, 2 ⅓, and 5 ⅛.
The core concept behind converting an improper fraction to a mixed number is to determine how many times the denominator goes into the numerator and express the remainder as a fraction.
Converting 11/5 to a Mixed Number: The Step-by-Step Process
Let's break down the conversion of 11/5 into a mixed number:
-
Division: Divide the numerator (11) by the denominator (5). 11 ÷ 5 = 2 with a remainder of 1.
-
Whole Number: The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 2.
-
Fraction: The remainder (1) becomes the numerator of the fractional part of the mixed number. The denominator remains the same (5). This gives us the fraction 1/5.
-
Combining: Combine the whole number and the fraction to form the mixed number. Therefore, 11/5 as a mixed number is 2 1/5.
Visual Representation: Understanding the Concept
Imagine you have 11 slices of pizza, and each pizza has 5 slices. You can make two whole pizzas (2 x 5 = 10 slices) with one slice remaining. This remaining slice represents the 1/5. Therefore, you have 2 whole pizzas and 1/5 of a pizza – 2 1/5. This visual representation helps solidify the understanding of the conversion process.
Practical Applications of Mixed Numbers
Mixed numbers are incredibly useful in various real-world scenarios:
-
Measurement: When measuring lengths, weights, or volumes, mixed numbers are commonly used. For instance, a board might measure 2 1/2 feet long, or a recipe might call for 1 ⅔ cups of flour.
-
Time: We use mixed numbers to express time. For example, 2 ½ hours or 1 ¼ hours.
-
Cooking and Baking: Recipes often utilize mixed numbers for precise ingredient measurements.
-
Construction and Engineering: Mixed numbers are essential for precise measurements and calculations in construction and engineering projects.
-
Everyday Calculations: Many everyday situations require the use of fractions, often expressed as mixed numbers for easier understanding.
Working with Mixed Numbers: Addition, Subtraction, Multiplication, and Division
Once you have converted an improper fraction to a mixed number, you can perform various arithmetic operations. However, it's often simpler to convert mixed numbers back into improper fractions before performing calculations, especially multiplication and division.
Converting Mixed Numbers back to Improper Fractions:
To convert a mixed number back to an improper fraction, follow these steps:
- Multiply: Multiply the whole number by the denominator. (In our example: 2 x 5 = 10)
- Add: Add the result to the numerator. (10 + 1 = 11)
- Keep the Denominator: Keep the original denominator. (5)
- Improper Fraction: The result is the improper fraction (11/5).
Further Examples of Improper Fraction to Mixed Number Conversion
Let's look at a few more examples to solidify your understanding:
-
17/3: 17 ÷ 3 = 5 with a remainder of 2. Therefore, 17/3 = 5 ⅔
-
23/6: 23 ÷ 6 = 3 with a remainder of 5. Therefore, 23/6 = 3 ⁵/₆
-
31/8: 31 ÷ 8 = 3 with a remainder of 7. Therefore, 31/8 = 3 ⁷/₈
-
100/12: 100 ÷ 12 = 8 with a remainder of 4. Therefore, 100/12 = 8 ⁴/₁₂ (This can be simplified to 8 ⅓)
Simplifying Fractions
Often, the resulting fraction in a mixed number can be simplified. For example, in the case of 100/12 simplified to 8 ⅓, the fraction ⁴/₁₂ can be reduced to ⅓ by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 4. Always simplify fractions to their lowest terms for clarity and ease of use.
The Importance of Mastering Fraction Conversion
The ability to convert between improper fractions and mixed numbers is a cornerstone of mathematical proficiency. It's a skill that underlies many more advanced concepts and is essential for success in various academic and professional fields. The more you practice, the more confident and efficient you'll become in performing these conversions. Regular practice and revisiting the concepts will ensure a solid grasp of this fundamental mathematical skill.
Beyond the Basics: Advanced Applications
While this guide focuses on the basic conversion of 11/5, the underlying principles extend to more complex scenarios involving larger numbers and different types of fractions. Understanding the core concepts presented here will provide a solid foundation for tackling these more advanced mathematical challenges. This includes working with fractions in algebra, calculus, and other advanced mathematical disciplines.
Conclusion: Mastering Fraction Conversions for Success
Converting 11/5 to the mixed number 2 1/5 is a straightforward process that involves division, identifying the whole number and the fractional part, and then combining them. This seemingly simple conversion is a crucial skill that underpins many mathematical operations and finds application in diverse real-world situations. By mastering this skill, you'll enhance your mathematical understanding and build a strong foundation for future learning and problem-solving. Remember to practice regularly and don't hesitate to revisit the steps and examples provided to reinforce your understanding. With consistent effort, you'll confidently navigate the world of fractions and mixed numbers.
Latest Posts
Latest Posts
-
Half Of 5 7 8 Inches
May 08, 2025
-
How Is 2 3 Not Always Equal To 4 6
May 08, 2025
-
What Is 2 3 Divided By 2 As A Fraction
May 08, 2025
-
Find The Radian Measure Of The Central Angle
May 08, 2025
-
Factors Of 225 That Add Up To 30
May 08, 2025
Related Post
Thank you for visiting our website which covers about 11 Over 5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.