23 5 As A Mixed Number
News Co
May 07, 2025 · 4 min read
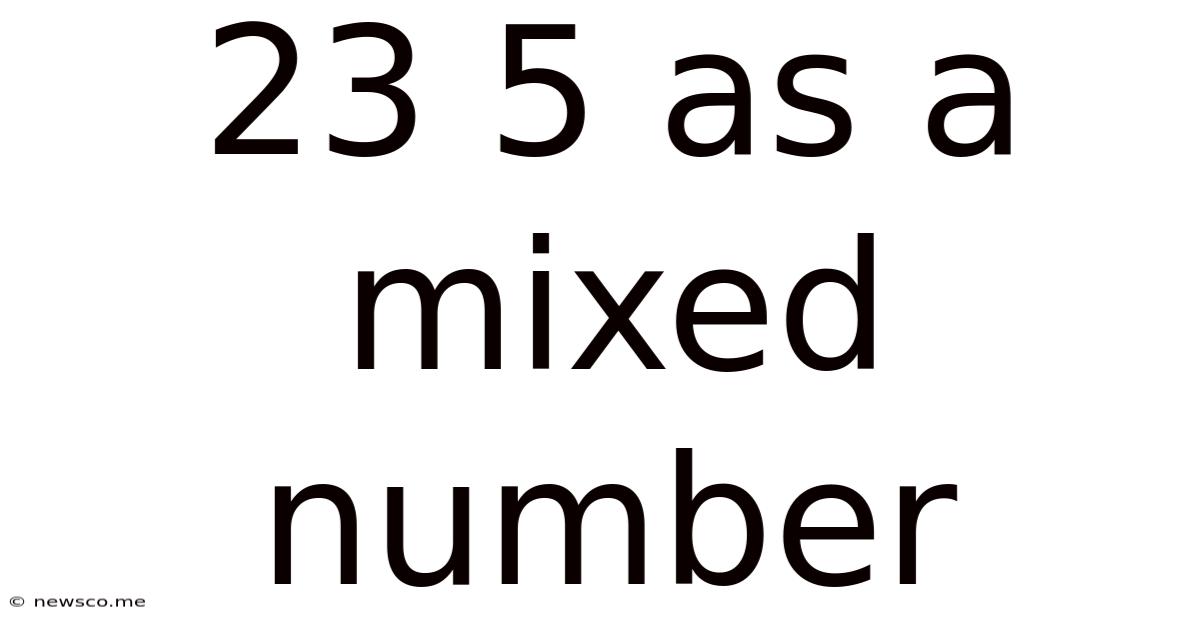
Table of Contents
23/5 as a Mixed Number: A Comprehensive Guide
Understanding fractions and how to convert them into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will delve deep into the process of converting the improper fraction 23/5 into a mixed number, explaining the concept in detail and providing various approaches to solve similar problems. We'll also explore the practical applications of mixed numbers and offer helpful tips and tricks to master this crucial mathematical concept.
What is a Mixed Number?
A mixed number is a number that combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾, 2 ⅔, and 5 ⅛ are all mixed numbers. They represent a quantity larger than one whole unit.
Converting Improper Fractions to Mixed Numbers
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. 23/5 is an improper fraction because 23 (the numerator) is larger than 5 (the denominator). To convert an improper fraction to a mixed number, we need to determine how many whole numbers are contained within the fraction and the remaining fractional part.
Methods for Converting 23/5 to a Mixed Number
There are several ways to convert 23/5 into a mixed number. Let's explore the most common methods:
Method 1: Division
The most straightforward method involves simple division. We divide the numerator (23) by the denominator (5):
23 ÷ 5 = 4 with a remainder of 3
The quotient (4) represents the whole number part of our mixed number. The remainder (3) becomes the numerator of the fractional part, and the denominator remains the same (5).
Therefore, 23/5 as a mixed number is 4 ⅗.
Method 2: Repeated Subtraction
This method involves repeatedly subtracting the denominator from the numerator until the result is less than the denominator.
- 23 - 5 = 18
- 18 - 5 = 13
- 13 - 5 = 8
- 8 - 5 = 3
We subtracted 5 four times, which gives us the whole number part (4). The remaining amount (3) is the numerator of the fraction, and the denominator remains 5. This again yields 4 ⅗.
Method 3: Visual Representation
While less practical for larger numbers, visualizing the fraction can be helpful for understanding the concept. Imagine 23/5 as 23 equal parts of a whole divided into 5 equal sections. Each 5 parts make up one whole. You can create 4 full sets of 5, leaving 3 parts remaining. This visually represents 4 ⅗.
Understanding the Concept: Why This Conversion is Important
Converting improper fractions to mixed numbers is crucial for several reasons:
-
Clarity and Understanding: Mixed numbers often provide a more intuitive and easily understandable representation of quantities than improper fractions. It's easier to grasp the concept of "4 and three-fifths" than "twenty-three-fifths."
-
Real-world Applications: Mixed numbers are frequently used in everyday life. Think about measuring ingredients for a recipe (2 ½ cups of flour), measuring distances (4 ¾ miles), or calculating time (1 ½ hours).
-
Mathematical Operations: While some calculations are easier with improper fractions, others are simpler with mixed numbers. Adding and subtracting mixed numbers can be more straightforward than dealing with their improper fraction equivalents.
-
Simplifying Calculations: Converting an improper fraction to a mixed number can simplify complex calculations, making them less prone to errors.
Practicing with Similar Problems
Let's solidify our understanding by working through a few more examples:
- Convert 17/4 to a mixed number:
17 ÷ 4 = 4 with a remainder of 1. Therefore, 17/4 = 4 ¼
- Convert 29/6 to a mixed number:
29 ÷ 6 = 4 with a remainder of 5. Therefore, 29/6 = 4 ⅚
- Convert 35/8 to a mixed number:
35 ÷ 8 = 4 with a remainder of 3. Therefore, 35/8 = 4 ⅜
Advanced Applications and Considerations
While converting simple improper fractions is relatively easy, larger numbers may require more complex calculations. However, the underlying principles remain the same: division and understanding remainders.
Consider the fraction 127/12. Using division:
127 ÷ 12 = 10 with a remainder of 7. Therefore, 127/12 = 10 ⁷⁄₁₂
Tips and Tricks for Success
-
Mastering Division: Proficiency in division is key to efficiently converting improper fractions to mixed numbers.
-
Practice Regularly: The more you practice, the more comfortable and confident you'll become.
-
Use Visual Aids: For beginners, visual aids like diagrams or fraction bars can be incredibly helpful.
-
Check Your Work: Always double-check your calculations to avoid errors. You can convert the mixed number back to an improper fraction to verify your answer.
Conclusion: Mastering Mixed Numbers for Mathematical Proficiency
Understanding how to convert improper fractions to mixed numbers is a cornerstone of mathematical literacy. This skill is not just essential for academic success but also for navigating everyday situations that involve fractions and measurements. By mastering the methods outlined in this guide and practicing regularly, you'll build a strong foundation in this fundamental mathematical concept and enhance your overall mathematical proficiency. Remember, the key lies in understanding the process of division, utilizing remainders effectively, and building confidence through consistent practice. From simple everyday tasks to complex mathematical problems, the ability to work confidently with mixed numbers will serve you well throughout your life.
Latest Posts
Latest Posts
-
What Is The Percentage Of 5 3
May 08, 2025
-
Find The Value Of X And Z Geometry
May 08, 2025
-
What Is 3 Of A Million
May 08, 2025
-
How To Write 15000 On A Check
May 08, 2025
-
Is 28 A Multiple Of 7
May 08, 2025
Related Post
Thank you for visiting our website which covers about 23 5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.