27 To The Power Of 2/3
News Co
Apr 05, 2025 · 6 min read
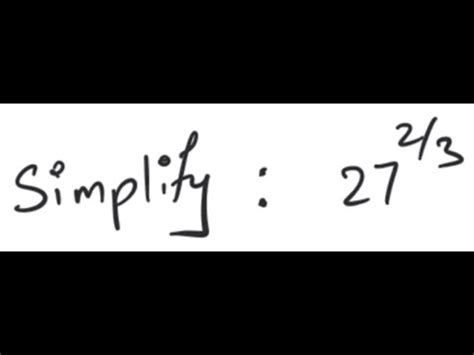
Table of Contents
Decoding 27 to the Power of 2/3: A Comprehensive Exploration
The seemingly simple mathematical expression, 27<sup>2/3</sup>, presents a fascinating opportunity to delve into the fundamentals of exponents, roots, and their practical applications. This exploration will go beyond simply calculating the answer; we'll dissect the underlying concepts, explore various approaches to solving the problem, and examine the broader implications within mathematics and beyond.
Understanding Exponents and Fractional Exponents
Before tackling 27<sup>2/3</sup> directly, let's establish a strong foundation in exponents. An exponent, or power, indicates how many times a number (the base) is multiplied by itself. For instance, 2<sup>3</sup> (2 to the power of 3) means 2 x 2 x 2 = 8.
Fractional exponents introduce a new layer of complexity. A fractional exponent, such as 2/3, combines the concepts of exponents and roots. The numerator represents the power, and the denominator represents the root. Therefore, 27<sup>2/3</sup> can be interpreted in two equivalent ways:
- (27<sup>1/3</sup>)<sup>2</sup>: This means we first find the cube root of 27 (the denominator is 3, indicating a cube root), and then we square the result (the numerator is 2, indicating a power of 2).
- (27<sup>2</sup>)<sup>1/3</sup>: Alternatively, we could first square 27, and then find the cube root of the result.
Calculating 27<sup>2/3</sup>: Step-by-Step Solutions
Let's explore both approaches:
Method 1: Cube Root First, then Square
-
Find the cube root of 27: What number, multiplied by itself three times, equals 27? The answer is 3 (3 x 3 x 3 = 27). Therefore, 27<sup>1/3</sup> = 3.
-
Square the result: Now, we square the cube root we found: 3<sup>2</sup> = 3 x 3 = 9.
Therefore, 27<sup>2/3</sup> = 9.
Method 2: Square First, then Cube Root
-
Square 27: 27<sup>2</sup> = 27 x 27 = 729.
-
Find the cube root of 729: What number, multiplied by itself three times, equals 729? The answer is 9 (9 x 9 x 9 = 729). Therefore, 729<sup>1/3</sup> = 9.
Therefore, 27<sup>2/3</sup> = 9.
Both methods yield the same result, confirming that 27<sup>2/3</sup> = 9.
Expanding the Understanding: Negative Exponents and Radicals
The concept of fractional exponents extends to negative exponents as well. A negative exponent indicates the reciprocal of the positive exponent. For instance, x<sup>-n</sup> = 1/x<sup>n</sup>. This principle applies to fractional exponents too. For example, 27<sup>-2/3</sup> = 1/27<sup>2/3</sup> = 1/9.
Furthermore, fractional exponents are intimately linked to radicals. The expression 27<sup>2/3</sup> can also be written as √∛27² This notation emphasizes the root and the power more explicitly. The cube root (∛) is applied first, followed by squaring.
Applications of Exponents and Roots in Various Fields
The concepts explored here—exponents, fractional exponents, and roots—are not merely abstract mathematical exercises. They find widespread applications in numerous fields, including:
1. Science and Engineering:
- Physics: Many physical phenomena, such as radioactive decay, population growth, and wave behavior, are modeled using exponential functions.
- Chemistry: Chemical reactions often involve exponential rate laws.
- Engineering: Exponential functions are crucial in circuit analysis, signal processing, and structural mechanics.
2. Finance and Economics:
- Compound Interest: The growth of money invested with compound interest is governed by exponential functions.
- Economic Growth: Economic models often utilize exponential functions to describe economic growth or decline.
3. Computer Science:
- Algorithms: The efficiency of many algorithms is expressed using exponential notation (e.g., O(2<sup>n</sup>)).
- Cryptography: Cryptography relies heavily on exponential functions for encryption and decryption.
4. Biology:
- Population Dynamics: Exponential functions are used to model population growth (or decay) in biological systems.
5. Statistics:
- Probability Distributions: Many probability distributions, like the exponential distribution and the normal distribution, are defined using exponential functions.
Beyond the Calculation: Exploring Mathematical Depth
While calculating 27<sup>2/3</sup> is relatively straightforward, the underlying concepts offer a gateway to deeper mathematical exploration. Understanding the relationship between exponents and roots allows us to tackle more complex expressions and fosters a stronger intuition for mathematical operations.
For example, consider the general case of a<sup>m/n</sup>, where 'a' is the base, and 'm/n' is the fractional exponent. This can be expressed as (a<sup>1/n</sup>)<sup>m</sup> or (a<sup>m</sup>)<sup>1/n</sup>, illustrating the interchangeability of the order of operations. This understanding is crucial when dealing with complex algebraic manipulations.
Furthermore, exploring irrational exponents, like π or e, introduces new challenges and opportunities for applying calculus and other advanced mathematical tools. The foundations laid by understanding simple expressions like 27<sup>2/3</sup> are essential for navigating these more intricate mathematical landscapes.
Practical Applications and Problem-Solving
Let's consider some practical scenarios where understanding 27<sup>2/3</sup> and similar concepts is vital:
Scenario 1: Volume of a Cube
Imagine a cube with a volume of 27 cubic units. To find the length of one side (s), we need to find the cube root of the volume: s = 27<sup>1/3</sup> = 3 units. Now, suppose we want to find the area of one face of this cube. The area of one face is s², which is 3² = 9 square units. This calculation inherently involves fractional exponents, although it may not be explicitly written as such.
Scenario 2: Scaling and Proportions
In design and engineering, scaling objects often involves fractional exponents. If we need to increase the volume of a similar object by a factor of 27<sup>2/3</sup> = 9, we can determine the scaling factor for each dimension. Since volume scales with the cube of the linear dimension, finding the cube root of 9 provides the scaling factor for each side length.
Scenario 3: Scientific Modeling
In many scientific models, exponential functions are used to describe growth or decay. Understanding the properties of fractional exponents allows scientists to manipulate and interpret these models effectively. For example, in analyzing radioactive decay, we might use fractional exponents to calculate the amount of a substance remaining after a specific time period.
Conclusion: The Significance of 27<sup>2/3</sup>
The seemingly simple calculation of 27<sup>2/3</sup> opens the door to a rich understanding of exponents, roots, and their interconnectedness. This exploration moves beyond a simple arithmetic solution to delve into the broader mathematical landscape and its practical applications in diverse fields. By grasping these fundamental concepts, we build a stronger foundation for tackling more complex mathematical problems and applying these principles to real-world situations. The number 9, the result of 27<sup>2/3</sup>, therefore represents not just a numerical answer but a key to unlocking deeper mathematical insights.
Latest Posts
Latest Posts
-
How To Find The Zeros Of A Cubic Function
Apr 05, 2025
-
What Is 6 Percent Of 8
Apr 05, 2025
-
What Are The Factors For 88
Apr 05, 2025
-
What Are The Prime Factors Of 225
Apr 05, 2025
-
Sum Of Interior Angles In A Heptagon
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about 27 To The Power Of 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
