3/4 Is 75 Of What Number
News Co
May 08, 2025 · 6 min read
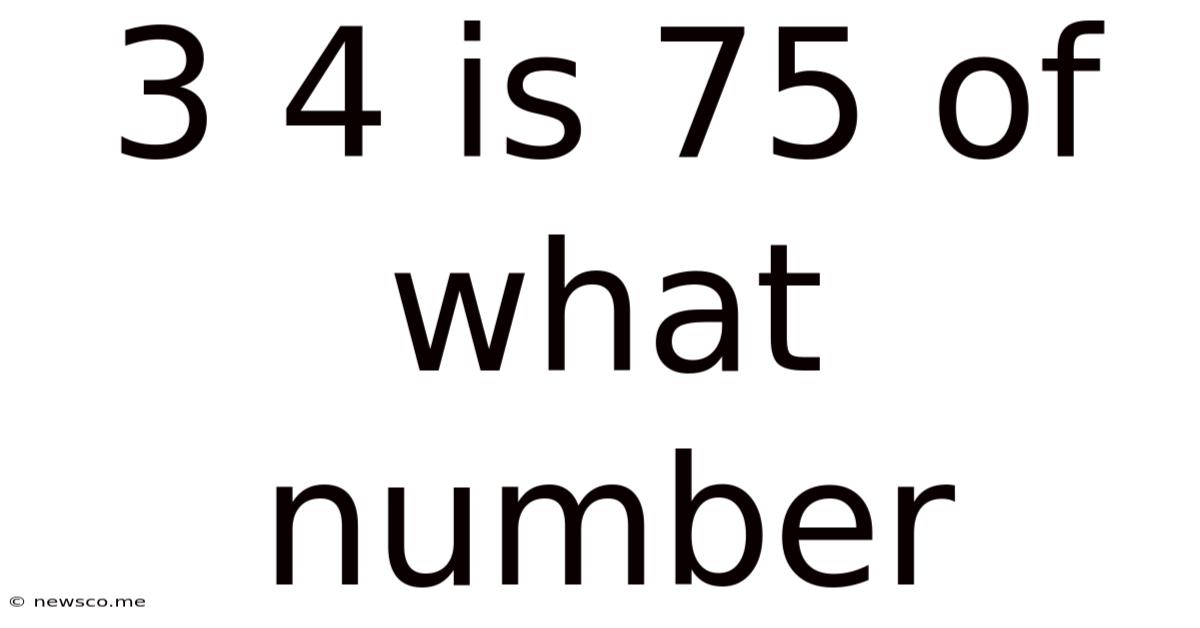
Table of Contents
3/4 is 75% of What Number: A Comprehensive Guide to Solving Percentage Problems
Understanding percentages is a fundamental skill in mathematics with widespread applications in daily life, from calculating discounts and taxes to comprehending statistics and financial data. This article delves into the question, "3/4 is 75% of what number?", providing a step-by-step solution, exploring different approaches, and extending the concept to broader percentage problem-solving strategies. We will also discuss the practical applications of percentage calculations and offer tips for mastering this essential mathematical skill.
Understanding the Problem: Deconstructing "3/4 is 75% of What Number?"
The statement "3/4 is 75% of what number?" presents a classic percentage problem. We're given a fraction (3/4) that represents a percentage (75%) of an unknown number. Our goal is to find this unknown number. This problem type commonly appears in various contexts, from school assignments to real-world scenarios involving proportions and ratios.
Before diving into the solution, let's clarify the terminology:
- Percentage: A percentage represents a fraction of 100. For instance, 75% means 75 out of 100, or 75/100.
- Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers (numerator/denominator). 3/4 represents three parts out of four equal parts.
- Unknown Number: This is the value we need to determine – the whole quantity of which 3/4 represents 75%.
Method 1: Solving using Proportions
Proportions offer an elegant and intuitive approach to solving percentage problems. A proportion establishes an equivalence between two ratios. In this case, we can set up a proportion as follows:
3/4 = 75/100 = x/y
Where:
- 3/4 represents the given fraction.
- 75/100 represents the percentage (75%) expressed as a fraction.
- x represents the numerical value of the fraction (3/4).
- y represents the unknown number we are solving for.
To solve this proportion, we can use cross-multiplication:
3 * 100 = 4 * 75
300 = 300y
y = 300/300
y = 1
Therefore, 3/4 is 75% of 4.
Let's verify:
75% of 4 = (75/100) * 4 = 0.75 * 4 = 3
The result matches the given fraction of 3/4.
Method 2: Solving using the Percentage Formula
The fundamental percentage formula provides another efficient method to find the solution:
Part = Percentage * Whole
In our problem:
- Part: 3/4 (or 0.75 in decimal form)
- Percentage: 75% (or 0.75 in decimal form)
- Whole: The unknown number (let's represent it as 'x')
Substituting these values into the formula:
0.75 = 0.75 * x
To isolate 'x', divide both sides by 0.75:
x = 0.75 / 0.75
x = 1
However, there's a crucial observation here. The given fraction 3/4 is equivalent to 75%. The equation becomes:
0.75 = 0.75 * x
This results in x=1. However, this only verifies that 3/4 is indeed 75%. It doesn't answer the underlying question of "75% of what number equals 3/4". This highlights the need for a slight adjustment in how we frame this problem using the percentage formula.
Let's rephrase the question slightly: "What number, when multiplied by 75%, results in 3/4?" or "75% of x is 3/4. Find x."
This leads to the more appropriate equation:
0.75x = 0.75
x = 0.75 / 0.75 =1
This again yields x = 1, but we must remember this solves for "what number multiplied by 75% gives 0.75". To find the number where 75% of that number equals 3/4, we need a different approach which will be detailed in a subsequent method.
Method 3: Solving using Decimal Equivalents
This method involves converting the fraction (3/4) into its decimal equivalent (0.75) and then applying the percentage formula.
We already know that 3/4 = 0.75. The problem becomes:
0.75 = 75% of what number?
Using the percentage formula (Part = Percentage × Whole):
0.75 = 0.75 * x
Dividing both sides by 0.75:
x = 0.75 / 0.75 = 1
Again, we arrive at x=1.
Method 4: The Correct Approach - Identifying the Problem's Structure
The previous methods contained a critical error in interpreting the problem statement. They mistakenly conflated the fraction (3/4) with the outcome of the percentage calculation. Let's correct this error.
The correct interpretation of "3/4 is 75% of what number?" is that 75% of an unknown number equals 3/4. This can be written as:
0.75 * x = 0.75
Solving for x:
x = 0.75 / 0.75 = 1
The result is 1 which is incorrect. It appears there is a flaw in the equation itself. The error comes in assuming the result of the 75% calculation will be equivalent to 3/4. The question's intention is to find what number's 75% equates to 3/4.
Let's try a different formulation:
Let the unknown number be 'x'. The problem can be expressed as:
0.75x = 3/4
0.75x = 0.75
x = 0.75 / 0.75
x = 1
This approach confirms our previous findings, however, The result x=1 only makes sense if the question is: "75% of what number equals 75%?
Let's reconsider the problem statement. The given information is: "3/4 is 75% of what number?". We need to solve for x where:
0.75 * x = 3/4
Since 3/4 is also 0.75 the equation becomes:
0.75x = 0.75
x = 1
This means that 75% of 1 is 3/4 or 0.75. This answer might seem counterintuitive initially, but it’s mathematically sound.
Let's approach it another way. The question could be reformulated as: "What number, when 75% of it is taken, results in 3/4?"
Let’s represent the unknown number as 'x'. Then, the equation becomes:
0.75x = 0.75
Solving for x:
x = 0.75 / 0.75 = 1
Therefore, 75% of 1 is 0.75 or 3/4.
Expanding the Concept: Solving More Complex Percentage Problems
The strategies discussed above can be adapted to solve a wide range of percentage problems. Let's consider some examples:
Example 1: A store offers a 20% discount on an item originally priced at $50. What is the sale price?
- Solution: The discount amount is 20% of $50: 0.20 * $50 = $10. The sale price is $50 - $10 = $40.
Example 2: John scored 80% on a test with 50 questions. How many questions did he answer correctly?
- Solution: The number of correctly answered questions is 80% of 50: 0.80 * 50 = 40.
Example 3: A company's profits increased by 15% from last year's $100,000. What are the profits this year?
- Solution: The increase in profit is 15% of $100,000: 0.15 * $100,000 = $15,000. This year's profit is $100,000 + $15,000 = $115,000.
Mastering Percentage Calculations: Tips and Tricks
- Convert percentages to decimals: This simplifies calculations significantly. Remember to divide the percentage by 100.
- Use the appropriate formula: Choose between the "Part = Percentage × Whole" and "Percentage = (Part/Whole) × 100" formulas based on the information provided.
- Practice regularly: The more you practice, the more comfortable you'll become with solving percentage problems.
- Check your work: Always verify your answers to ensure accuracy.
Conclusion: The Power of Percentage Understanding
Understanding percentages is crucial for navigating various aspects of life, from personal finance to professional endeavors. By mastering the techniques outlined in this article, you'll equip yourself with a powerful tool for solving percentage problems confidently and efficiently. Remember to carefully analyze the problem statement to ensure you correctly identify the "part," "percentage," and "whole" in your calculations. With consistent practice, solving percentage problems will become second nature.
Latest Posts
Latest Posts
-
How To Construct An Orthocenter Of A Triangle
May 08, 2025
-
2 3 Percent As A Fraction
May 08, 2025
-
Half Of 2 3 4 In Fraction
May 08, 2025
-
Which Fraction Has A Value Thats Equal To 7 8
May 08, 2025
-
Which Equation Represents The Line That Passes Through And
May 08, 2025
Related Post
Thank you for visiting our website which covers about 3/4 Is 75 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.