30 Is 10 Of What Number
News Co
May 07, 2025 · 4 min read
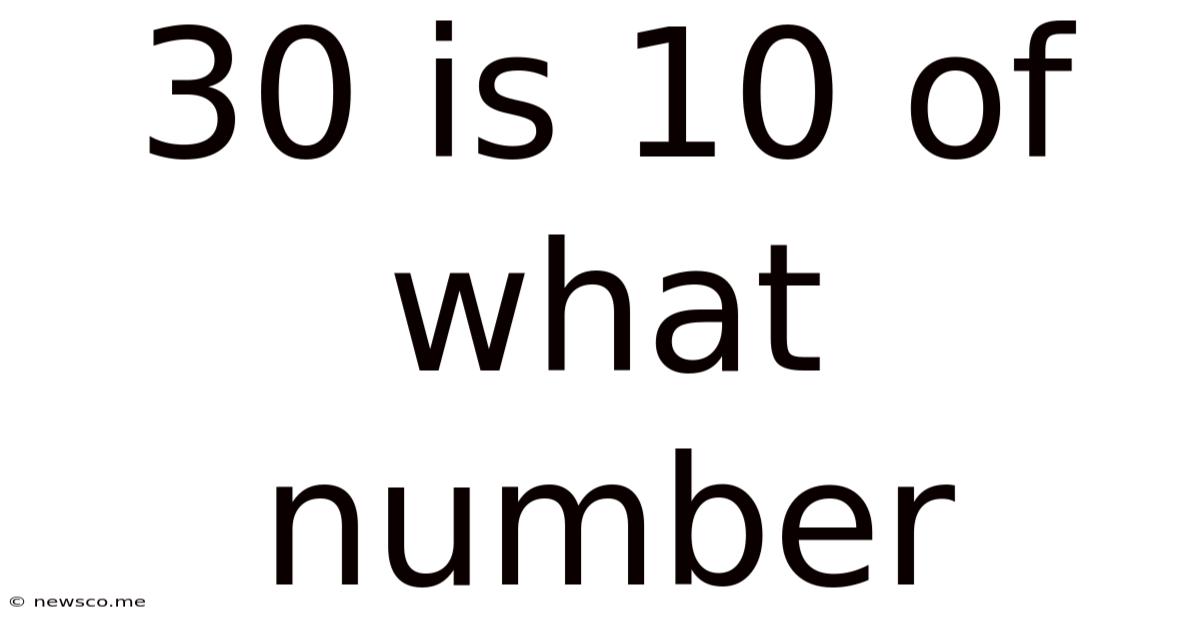
Table of Contents
30 is 10% of What Number? Solving Percentage Problems
Many everyday situations require understanding percentages. Whether you're calculating discounts, figuring out tips, or analyzing financial data, knowing how to work with percentages is a crucial skill. This article will delve into how to solve the classic percentage problem: "30 is 10% of what number?". We'll explore multiple methods, providing a comprehensive understanding of the underlying concepts and offering practical applications.
Understanding the Problem
The question, "30 is 10% of what number?", is a percentage problem where we know the percentage (10%) and the resulting value (30), but we need to find the original number. This original number is often referred to as the "base" or "whole". Let's break it down:
- Percentage: 10% (This represents a fraction of the whole).
- Part: 30 (This is the portion of the whole represented by the percentage).
- Whole: This is the unknown value we need to find (Let's represent it with 'x').
Method 1: Using the Percentage Formula
The most common approach to solving percentage problems involves the basic percentage formula:
(Part / Whole) * 100% = Percentage
We can rearrange this formula to solve for the unknown "Whole":
Whole = (Part / Percentage) * 100
Plugging in our known values:
x = (30 / 10) * 100
x = 3 * 100
x = 300
Therefore, 30 is 10% of 300.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. A proportion sets two ratios equal to each other. In this case, we can set up a proportion as follows:
10/100 = 30/x
This proportion states that the ratio of 10 (the percentage) to 100 (the whole representing 100%) is equal to the ratio of 30 (the part) to x (the unknown whole).
To solve this proportion, we can cross-multiply:
10 * x = 30 * 100
10x = 3000
x = 3000 / 10
x = 300
Again, we find that 30 is 10% of 300.
Method 3: Using Decimal Equivalents
Percentages can also be expressed as decimals. 10% is equivalent to 0.10 (or simply 0.1). We can rewrite the problem as:
0.1 * x = 30
To solve for x, we divide both sides of the equation by 0.1:
x = 30 / 0.1
x = 300
This method provides a concise and straightforward solution.
Practical Applications: Real-World Examples
Understanding percentage calculations is essential for various real-world applications:
1. Sales and Discounts:
Imagine a store is offering a 10% discount on an item priced at $300. To find the discount amount, you calculate 10% of $300, which is $30 (as we've already established). The final price after the discount would be $300 - $30 = $270.
2. Taxes and Interest:
Calculating sales tax or interest earned on savings accounts often involves percentages. For instance, if you earn 10% interest on a $300 investment, you'd earn $30 in interest.
3. Tip Calculations:
When calculating tips in restaurants, you typically use percentages. A 10% tip on a $300 bill would be $30.
4. Financial Analysis:
Percentage changes are frequently used in financial analysis to track the performance of investments or businesses. For instance, a 10% increase in profit would be calculated based on the previous profit figure.
5. Surveys and Statistics:
Percentages are fundamental to representing data in surveys and statistics. For example, if 30 out of 300 respondents answered "yes" to a question, this represents 10% of the total respondents.
Expanding the Concept: Different Percentages and Values
Let's explore how to solve similar problems with different percentage values and resulting amounts. The methods outlined above remain consistent.
Example 1: 60 is 20% of what number?
Using the formula:
x = (60 / 20) * 100 = 300
Example 2: 15 is 5% of what number?
Using the formula:
x = (15 / 5) * 100 = 300
Example 3: 75 is 25% of what number?
Using the formula:
x = (75 / 25) * 100 = 300
Notice that despite different percentage values and resulting amounts, the underlying method remains the same. The key is to correctly identify the "part," "percentage," and "whole" in the problem.
Advanced Applications: Compound Interest and Growth Rates
Percentage calculations extend beyond simple scenarios to more complex applications like compound interest and growth rates. Compound interest involves calculating interest on both the principal amount and accumulated interest. Growth rates represent the percentage change over time. Understanding these concepts is crucial in personal finance and business.
Conclusion: Mastering Percentage Calculations
Mastering percentage calculations is a valuable skill with wide-ranging applications. By understanding the different methods – using the formula, proportions, or decimal equivalents – you can confidently tackle various percentage problems encountered in daily life, finance, and other fields. Remember to clearly identify the "part," "percentage," and "whole" in each problem to ensure accurate calculations. Practice is key to developing proficiency in this fundamental mathematical concept. The ability to quickly and accurately calculate percentages will improve your problem-solving skills and empower you to make informed decisions across various aspects of life.
Latest Posts
Latest Posts
-
What Does The Word By Mean In Math
May 08, 2025
-
Can A Rhombus Be A Trapezoid
May 08, 2025
-
11 Divided By 3 As A Fraction
May 08, 2025
-
How Do You Find The Distance Between Two Parallel Lines
May 08, 2025
-
Round 7 5791 To The Nearest Hundredth
May 08, 2025
Related Post
Thank you for visiting our website which covers about 30 Is 10 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.