4 Divided By 3 In A Fraction
News Co
May 08, 2025 · 5 min read
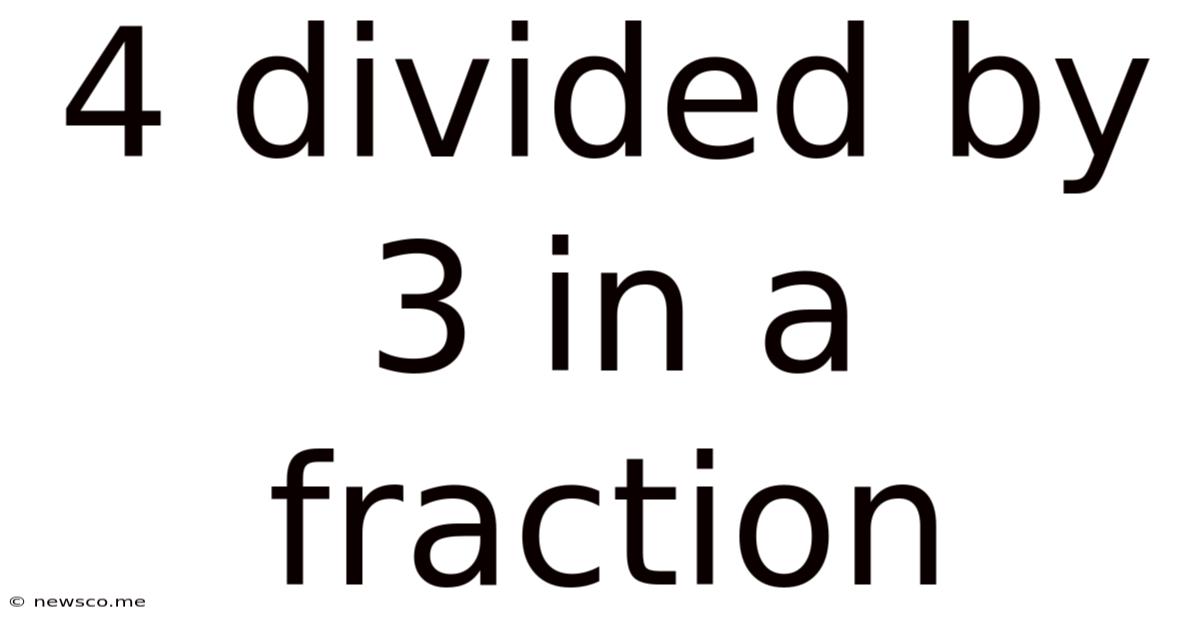
Table of Contents
4 Divided by 3 in a Fraction: A Deep Dive into Division and Fractions
Understanding how to express division as a fraction is a fundamental concept in mathematics. This article delves deep into the seemingly simple problem of 4 divided by 3 as a fraction, exploring the underlying principles, different approaches, and practical applications. We'll go beyond the simple answer and explore the nuances of fraction representation, its implications in various mathematical contexts, and how to effectively communicate this concept.
Understanding Division and Fractions
Before tackling 4 divided by 3, let's establish a strong foundation. Division is the process of splitting a quantity into equal parts. Think of it as sharing something equally amongst a group. A fraction, on the other hand, represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, the fraction 1/2 (one-half) represents one part out of two equal parts. Similarly, 3/4 (three-quarters) represents three parts out of four equal parts.
Expressing 4 Divided by 3 as a Fraction
The problem "4 divided by 3" can be written as a fraction directly. The dividend (the number being divided, 4) becomes the numerator, and the divisor (the number dividing, 3) becomes the denominator. Therefore:
4 ÷ 3 = 4/3
This fraction, 4/3, is an improper fraction because the numerator (4) is larger than the denominator (3). Improper fractions represent values greater than one.
Converting an Improper Fraction to a Mixed Number
Improper fractions are often converted into mixed numbers for easier understanding and interpretation. A mixed number combines a whole number and a proper fraction. To convert 4/3 to a mixed number:
- Divide the numerator by the denominator: 4 ÷ 3 = 1 with a remainder of 1.
- The quotient (1) becomes the whole number part of the mixed number.
- The remainder (1) becomes the numerator of the fraction part, and the denominator remains the same (3).
Therefore, 4/3 is equivalent to 1 1/3. This means one whole unit and one-third of another unit.
Visualizing the Fraction
Imagine you have 4 pizzas. You want to share these pizzas equally among 3 people. Each person receives 4/3 or 1 1/3 pizzas. This visual representation solidifies the concept of an improper fraction and its mixed number equivalent.
Practical Applications of 4/3
The fraction 4/3, or its equivalent 1 1/3, appears in various real-world scenarios:
- Recipe Scaling: A recipe calls for 3 cups of flour, but you want to make a larger batch, using 4 cups. The ratio of the new amount to the original amount is 4/3.
- Measurement Conversions: Converting between different units of measurement, like inches and centimeters, can often involve fractions like 4/3.
- Geometry: Calculating areas and volumes of shapes sometimes results in improper fractions such as 4/3. For example, the volume of a sphere has pi as a factor and involves improper fractions depending on the dimensions.
- Data Analysis: Representing proportions or ratios in data analysis often involves fractions, sometimes yielding improper fractions.
Further Exploration: Decimal Representation
The fraction 4/3 can also be expressed as a decimal. To do this, divide the numerator (4) by the denominator (3):
4 ÷ 3 ≈ 1.333...
The decimal representation is a repeating decimal, with the digit 3 repeating infinitely. This is denoted by a bar over the repeating digit (1.3̅).
Comparing and Ordering Fractions
Understanding the concept of 4/3 allows us to effectively compare and order fractions. For example, we can easily see that 4/3 is greater than 1 but less than 2. The ability to compare fractions is crucial in various mathematical applications and problem-solving scenarios.
Solving Problems Involving 4/3
Let's explore a few example problems that involve 4/3:
Example 1: A painter needs 3 liters of paint to cover a wall. How many liters of paint are needed to cover 4 such walls?
Solution: To cover 4 walls, the painter needs 4 * 3 = 12 liters of paint. This can also be represented as a ratio: (4 walls) / (1 wall) = 4/1. So the total paint required is 4/1 * 3 liters = 12 liters.
Example 2: A recipe calls for 3 cups of sugar. If you want to make 1 1/3 times the recipe, how much sugar do you need?
Solution: You need 1 1/3 * 3 cups of sugar = (4/3) * 3 cups = 4 cups of sugar.
Example 3: A rectangular box has a length of 4 meters and a width of 3 meters. The length to width ratio of this box is 4/3.
Solution: The ratio 4/3 implies that the length of the box is 4/3 times its width. This ratio remains constant regardless of the actual values of length and width.
These examples illustrate the versatility of the fraction 4/3 and its relevance in various problem-solving contexts.
Conclusion: The Significance of 4/3
The seemingly simple fraction 4/3, representing 4 divided by 3, unlocks a world of mathematical understanding. Its representation as an improper fraction, its conversion to a mixed number, and its decimal equivalent showcase the interconnectedness of different mathematical concepts. From practical applications in everyday life to more complex mathematical problems, understanding 4/3, and fractions in general, is essential for building a solid mathematical foundation. Mastering this concept opens doors to further exploration of more advanced mathematical ideas and problem-solving techniques. The ability to represent division as a fraction, whether it's a proper or improper fraction, is a key skill that transcends simple arithmetic, impacting various fields from cooking to engineering. Through visual representations, practical examples, and a deep understanding of the underlying principles, the seemingly simple act of dividing 4 by 3 unveils a wealth of mathematical insights.
Latest Posts
Latest Posts
-
What Is Half Of 3 And 1 4
May 08, 2025
-
Cannot Be Measured Ray Or Line Segment
May 08, 2025
-
Completing The Square To Find The Vertex
May 08, 2025
-
2 3 5 7 11 13 17 19 23 29
May 08, 2025
-
Use The Graph To Find The Following
May 08, 2025
Related Post
Thank you for visiting our website which covers about 4 Divided By 3 In A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.