4 Of What Number Is 5
News Co
May 08, 2025 · 5 min read
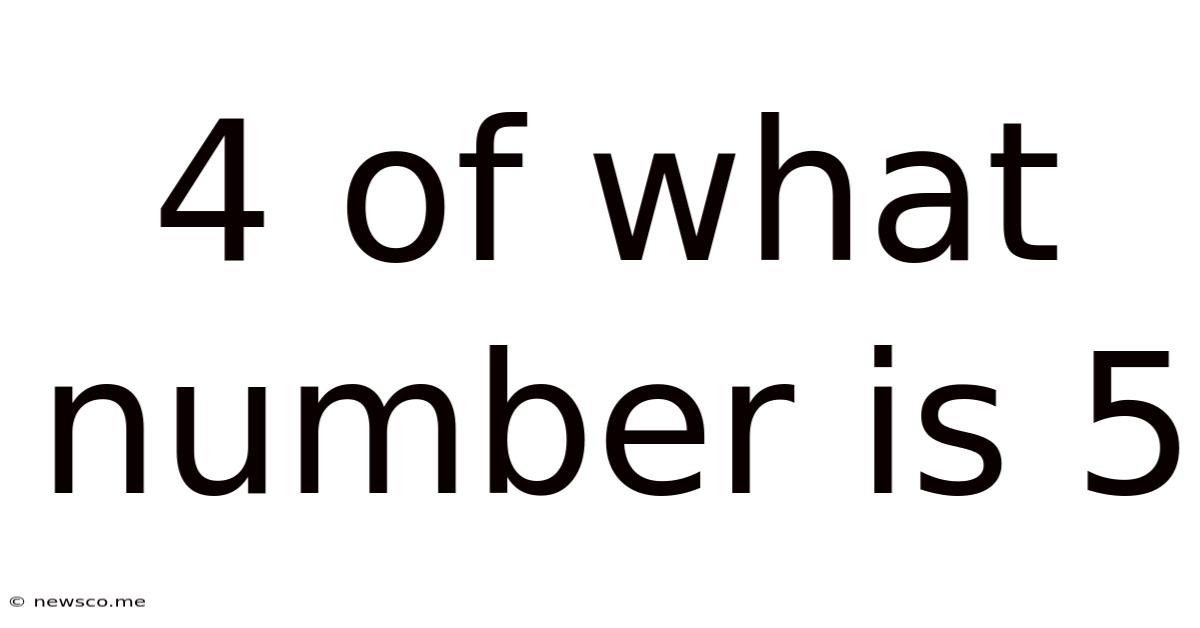
Table of Contents
4 Times What Number is 5? Unpacking a Simple Equation and its Broader Implications
The seemingly simple question, "4 times what number is 5?", hides a wealth of mathematical concepts and practical applications. At its core, it's a basic algebraic equation, but exploring its solution reveals fundamental principles applicable across various fields, from elementary arithmetic to advanced calculus and even real-world problem-solving. This article will delve into the solution, explore the underlying concepts, and showcase the broader implications of such seemingly simple mathematical problems.
Solving the Equation: A Step-by-Step Guide
The question, "4 times what number is 5?", can be translated into an algebraic equation:
4x = 5
Where 'x' represents the unknown number we're trying to find. To solve for 'x', we need to isolate it on one side of the equation. This involves using inverse operations. Since 'x' is being multiplied by 4, we perform the inverse operation – division – on both sides of the equation:
4x / 4 = 5 / 4
This simplifies to:
x = 1.25
Therefore, 4 times 1.25 is 5.
Understanding the Fundamentals: Multiplication and Division
The solution relies heavily on the fundamental arithmetic operations of multiplication and division. Multiplication is repeated addition; 4 x 1.25 means adding 1.25 four times: 1.25 + 1.25 + 1.25 + 1.25 = 5. Division is the inverse of multiplication; it finds how many times one number is contained within another. In our equation, dividing 5 by 4 tells us how many times 4 fits into 5 (1.25 times).
The Commutative Property of Multiplication
It's crucial to understand that multiplication is commutative, meaning the order of the numbers doesn't affect the result. 4 x 1.25 is the same as 1.25 x 4. This property simplifies calculations and helps in understanding the relationship between the numbers involved.
Beyond the Basics: Exploring Fractions and Decimals
Our solution, 1.25, is expressed as a decimal. However, it can also be represented as a fraction:
5/4
This fractional representation highlights the division inherent in the problem. The numerator (5) represents the total value, and the denominator (4) represents the number of parts we're dividing it into. Understanding fractions is essential for comprehending ratios, proportions, and various other mathematical concepts. Converting between decimals and fractions is a valuable skill for solving diverse problems.
Working with Fractions: A Practical Example
Imagine you have 5 pizzas to share equally among 4 friends. Each friend would receive 5/4 or 1.25 pizzas. This simple example demonstrates how fractions and decimals can solve real-world problems involving division and sharing.
Applications in Various Fields: From Finance to Physics
The ability to solve equations like "4x = 5" isn't confined to abstract mathematical exercises. It has far-reaching applications across various fields:
-
Finance: Calculating interest rates, determining loan payments, and analyzing investment returns often involve solving similar algebraic equations.
-
Physics: Many physical phenomena are described using mathematical equations. Calculating velocity, acceleration, force, or energy often requires solving for unknown variables, similar to our example.
-
Engineering: Engineers use mathematics extensively in designing and building structures, analyzing stresses and strains, and optimizing designs. Solving algebraic equations is a fundamental tool in their work.
-
Computer Science: Programming and algorithms rely heavily on mathematical logic and problem-solving skills. Solving equations is crucial for creating efficient and accurate programs.
-
Chemistry: Stoichiometry, the study of quantitative relationships between reactants and products in chemical reactions, involves solving equations to determine the amounts of substances involved.
Advanced Concepts: Linear Equations and Beyond
Our simple equation, 4x = 5, is an example of a linear equation – an equation where the highest power of the unknown variable (x) is 1. Linear equations are fundamental building blocks in algebra and are used extensively in more complex mathematical models. Understanding how to solve linear equations provides a strong foundation for tackling more advanced mathematical concepts, such as:
-
Simultaneous Equations: Solving multiple equations with multiple unknown variables.
-
Quadratic Equations: Equations where the highest power of the variable is 2.
-
Calculus: Calculus involves studying rates of change and accumulation, and solving equations is essential for analyzing and understanding these concepts.
Developing Problem-Solving Skills: A Crucial Life Skill
The ability to solve mathematical problems, even seemingly simple ones like "4 times what number is 5?", is a crucial life skill. It's not just about memorizing formulas; it's about developing a systematic approach to problem-solving, involving:
-
Understanding the problem: Clearly identifying what is being asked.
-
Formulating an equation: Translating the problem into mathematical language.
-
Solving the equation: Applying appropriate techniques to find the unknown variable.
-
Interpreting the solution: Understanding the meaning of the solution in the context of the original problem.
These problem-solving skills are transferable and applicable far beyond the realm of mathematics. They are valuable tools for tackling challenges in any aspect of life, from personal finance to career planning.
Conclusion: The Power of Simple Equations
The seemingly simple question, "4 times what number is 5?", serves as a gateway to a vast world of mathematical concepts and their practical applications. By exploring its solution, we've touched upon fundamental arithmetic operations, fractions, decimals, linear equations, and the broader importance of problem-solving skills. Understanding and mastering these concepts empowers us to tackle more complex challenges and enhances our ability to solve problems across diverse fields. The power of simple equations lies not just in their immediate solutions, but in the foundational knowledge and problem-solving abilities they cultivate. It's a reminder that even the most basic mathematical concepts can have profound and far-reaching implications.
Latest Posts
Latest Posts
-
What Is 5 8 As A Grade
May 09, 2025
-
How To Find A Gcf Using Prime Factorization
May 09, 2025
-
A Rhombus Is A Parallelogram With
May 09, 2025
-
What Expression Is Equivalent To 3 5
May 09, 2025
-
A Rhombus Is A Quadrilateral
May 09, 2025
Related Post
Thank you for visiting our website which covers about 4 Of What Number Is 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.