413 Divided By 2 With Remainder
News Co
May 08, 2025 · 5 min read
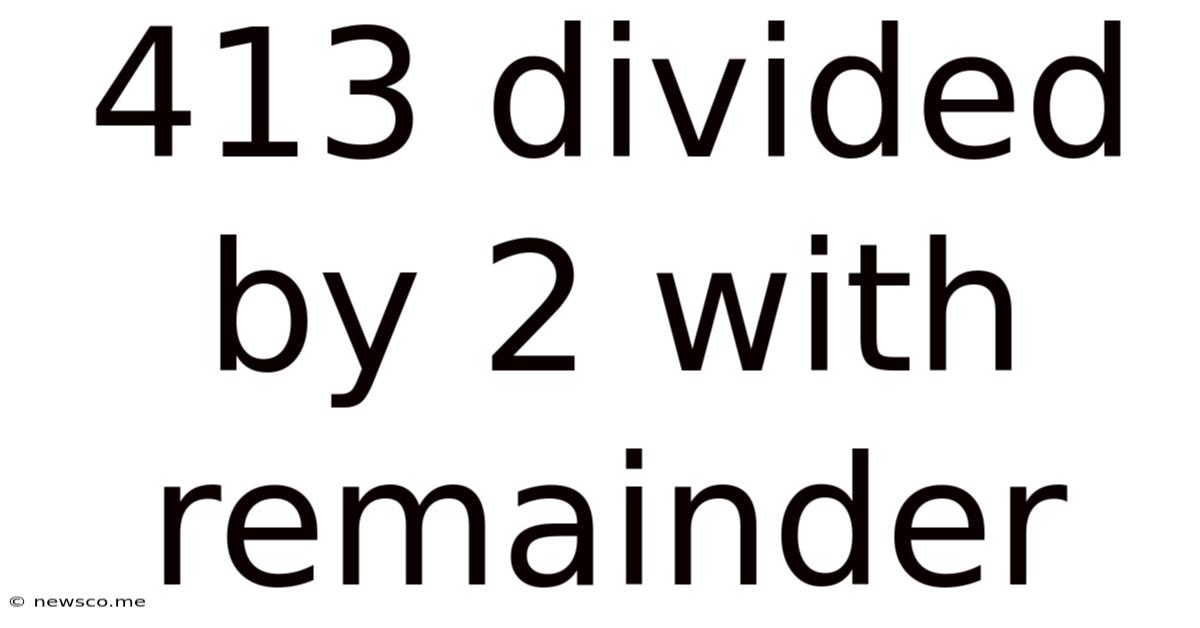
Table of Contents
413 Divided by 2 with Remainder: A Deep Dive into Division and Remainders
The seemingly simple question, "What is 413 divided by 2 with the remainder?", opens a door to a fascinating exploration of fundamental mathematical concepts. While the answer itself is straightforward, the underlying principles and their applications extend far beyond basic arithmetic. This article will delve into the process of division with remainders, explore its practical uses, and touch upon related mathematical ideas. We'll examine various methods of solving this problem, and even look at how this seemingly simple calculation finds relevance in advanced mathematical fields and computer science.
Understanding Division and Remainders
Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity (the dividend) into equal parts (the divisor). When the dividend isn't perfectly divisible by the divisor, we're left with a remainder – a value representing the amount left over after the division process.
In the context of 413 divided by 2, we can represent this mathematically as:
413 ÷ 2 = 206 with a remainder of 1
This means that 413 can be divided into 206 groups of 2, with 1 left over.
The Long Division Method
The long division method is a classical approach to solving division problems, particularly those involving larger numbers. Let's work through 413 ÷ 2 using this method:
-
Set up: Write the dividend (413) inside the long division symbol and the divisor (2) outside.
-
Divide: Start by dividing the first digit of the dividend (4) by the divisor (2). 4 ÷ 2 = 2. Write the quotient (2) above the 4.
-
Multiply: Multiply the quotient (2) by the divisor (2): 2 x 2 = 4. Write this result below the 4.
-
Subtract: Subtract the result (4) from the digit above it (4): 4 - 4 = 0.
-
Bring down: Bring down the next digit from the dividend (1).
-
Repeat: Divide 1 by 2. Since 1 is smaller than 2, the quotient is 0. Write 0 above the 1.
-
Multiply and Subtract: Multiply 0 by 2 (which is 0) and subtract it from 1. This leaves 1.
-
Bring down: Bring down the next digit (3).
-
Repeat: Now we have 13. Divide 13 by 2: 13 ÷ 2 = 6 with a remainder of 1. Write 6 above the 3.
-
Multiply and Subtract: Multiply 6 by 2 (which is 12) and subtract it from 13: 13 - 12 = 1. This is our remainder.
Therefore, the long division shows us that 413 ÷ 2 = 206 with a remainder of 1.
Applications of Division with Remainders
The concept of division with remainders isn't just an abstract mathematical exercise; it has numerous practical applications across various fields.
Everyday Life
-
Sharing: Imagine sharing 413 candies amongst 2 friends. Each friend gets 206 candies, and you have 1 candy left.
-
Grouping: If you have 413 books and want to arrange them into stacks of 2, you'll have 206 stacks with one book remaining.
-
Measurement: Consider cutting a 413-centimeter ribbon into 2-centimeter pieces. You'll get 206 pieces, with a 1-centimeter piece left over.
Computer Science
Remainders play a crucial role in computer science:
-
Modulo Operator (%): Programming languages use the modulo operator (%) to find the remainder of a division. In many programming languages,
413 % 2would return 1. -
Hashing: Hashing algorithms, used in data structures like hash tables, often utilize the modulo operator to distribute data efficiently across different memory locations.
-
Cryptography: Modular arithmetic, which heavily relies on remainders, forms the foundation of many cryptographic systems.
Advanced Mathematics
-
Modular Arithmetic: This branch of number theory studies the remainders after division. It has applications in cryptography, coding theory, and other areas.
-
Group Theory: Concepts related to division and remainders are fundamental in group theory, a significant area of abstract algebra.
-
Number Theory: Many number-theoretic problems involve finding remainders or determining divisibility properties.
Exploring Related Concepts
Understanding division with remainders helps us grasp related mathematical concepts:
Divisibility Rules
Divisibility rules provide quick ways to determine if a number is divisible by another number without performing long division. For example, a number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8). Since 413 ends in 3 (an odd number), it's not perfectly divisible by 2.
Prime and Composite Numbers
A prime number is only divisible by 1 and itself. A composite number is divisible by more than just 1 and itself. The remainder when dividing by 2 helps us identify whether a number is potentially prime (if the remainder is 1) or definitely composite (if the remainder is 0).
Factors and Multiples
Factors are numbers that divide a given number without leaving a remainder. Multiples are the result of multiplying a number by an integer. Understanding remainders can assist in finding factors and multiples.
Beyond 413 ÷ 2: Expanding the Scope
The principles discussed here apply to any division problem involving a remainder. Let's consider some variations:
Larger Numbers
Dividing larger numbers with remainders simply requires extending the long division method. The underlying concepts remain the same.
Different Divisors
The divisor doesn't have to be 2. We can apply the same process to divide 413 by any other number.
Decimal Remainders
Sometimes, instead of expressing the remainder as a whole number, it can be expressed as a decimal fraction. For example, 413 divided by 3 would result in a decimal remainder.
Conclusion
While the initial question of 413 divided by 2 with a remainder may seem basic, it serves as a gateway to understanding fundamental concepts within mathematics and computer science. From everyday applications to advanced mathematical fields, the ability to perform division with remainders and grasp its underlying principles is an essential skill. The long division method provides a systematic approach to finding the quotient and remainder, while the modulo operator offers a concise way to obtain the remainder in programming. Furthermore, an understanding of this concept paves the way for deeper explorations into more advanced areas like modular arithmetic and number theory. By mastering division with remainders, we unlock a wide range of applications and capabilities across multiple disciplines.
Latest Posts
Latest Posts
-
2 Step Word Problems 5th Grade
May 08, 2025
-
4 Of What Number Is 5
May 08, 2025
-
What Is The Modulus Of 6 7i
May 08, 2025
-
Are Rational Numbers Closed Under Subtraction
May 08, 2025
-
How Can I Use Math In Everyday Life
May 08, 2025
Related Post
Thank you for visiting our website which covers about 413 Divided By 2 With Remainder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.