51 8 As A Mixed Number
News Co
May 07, 2025 · 5 min read
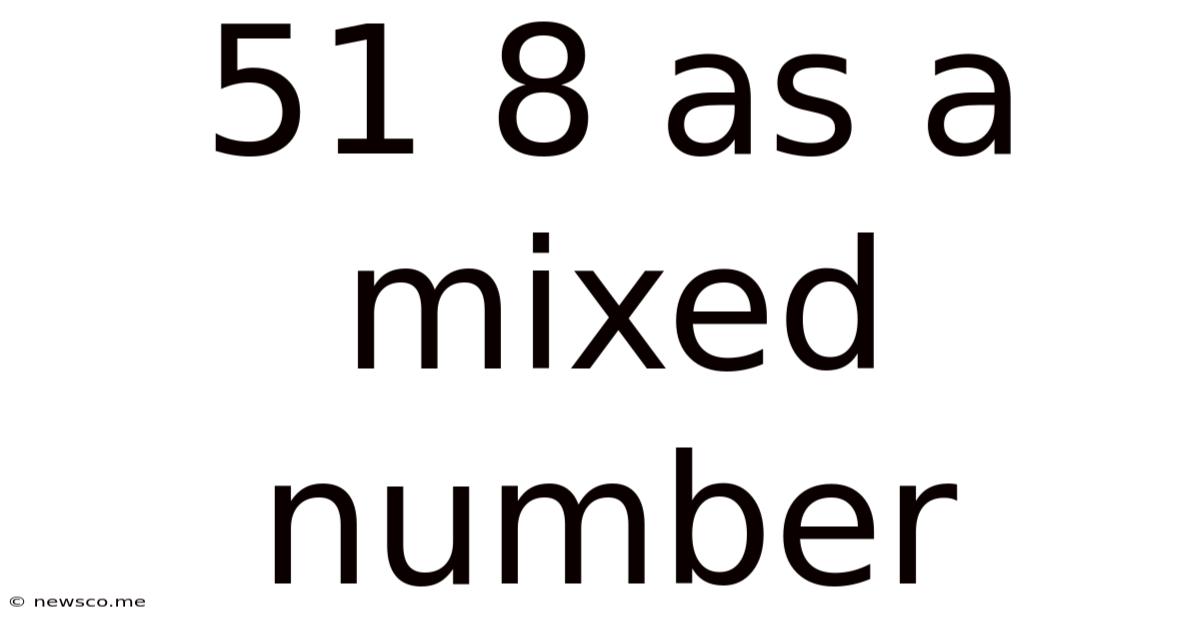
Table of Contents
51/8 as a Mixed Number: A Comprehensive Guide
Understanding how to convert improper fractions, like 51/8, into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will not only show you how to convert 51/8 into a mixed number but will also delve into the underlying concepts, provide alternative methods, and offer practical applications. We’ll explore the process step-by-step, ensuring you gain a solid grasp of this essential mathematical operation.
What is a Mixed Number?
Before diving into the conversion, let's clarify what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number; it represents two whole units and three-quarters of another unit.
Converting 51/8 to a Mixed Number: The Standard Method
The most common method for converting an improper fraction (like 51/8, where the numerator is larger than the denominator) to a mixed number involves division. Here's how it works:
-
Divide the numerator by the denominator: Divide 51 by 8.
- 51 ÷ 8 = 6 with a remainder of 3.
-
The quotient becomes the whole number: The quotient (6) becomes the whole number part of your mixed number.
-
The remainder becomes the numerator: The remainder (3) becomes the numerator of the fractional part.
-
The denominator stays the same: The denominator (8) remains unchanged.
Therefore, 51/8 as a mixed number is 6 ¾.
Visualizing the Conversion
Imagine you have 51 pieces of pizza, and you want to divide them into groups of 8 (because the denominator is 8). You can form 6 complete groups of 8, leaving you with 3 pieces leftover. These 6 full groups represent the whole number (6), and the remaining 3 pieces represent the fraction (3/8). Hence, you have 6 ¾ groups of pizza.
Alternative Method: Repeated Subtraction
While division is the most efficient, you can also use repeated subtraction to convert 51/8 into a mixed number. This method is helpful for understanding the concept more intuitively:
-
Repeatedly subtract the denominator from the numerator: Subtract 8 from 51 repeatedly until you get a number less than 8.
- 51 - 8 = 43
- 43 - 8 = 35
- 35 - 8 = 27
- 27 - 8 = 19
- 19 - 8 = 11
- 11 - 8 = 3
-
Count the number of subtractions: You performed the subtraction 6 times. This is your whole number.
-
The remaining number is the numerator: The remaining number after the subtractions (3) is your numerator.
-
The denominator remains the same: The denominator remains 8.
Again, this gives us the mixed number 6 ¾.
Practical Applications of Converting Improper Fractions to Mixed Numbers
Converting improper fractions to mixed numbers is essential in various real-world scenarios:
-
Cooking and Baking: Recipes often use mixed numbers to represent ingredient quantities (e.g., 2 ½ cups of flour). Understanding the conversion allows you to accurately measure ingredients.
-
Measurement: Mixed numbers are frequently used in measuring lengths, weights, and volumes. Converting an improper fraction to a mixed number provides a clearer understanding of the measurement.
-
Construction and Engineering: Precision is crucial in construction and engineering. Converting improper fractions to mixed numbers helps in accurately calculating dimensions and materials needed for a project.
-
Data Analysis: In data analysis, presenting data as mixed numbers can often be more intuitive and easier to understand than improper fractions.
-
Everyday Life: Many everyday situations involve fractions, whether it’s sharing pizza, measuring fabric, or calculating fuel consumption. Converting improper fractions to mixed numbers helps simplify these calculations.
Importance of Understanding Fractions and Mixed Numbers
A strong understanding of fractions and mixed numbers is vital for success in higher-level mathematics and various fields. It lays the groundwork for more advanced concepts, such as:
-
Decimals: Converting fractions to decimals and vice versa requires a solid understanding of fraction manipulation.
-
Algebra: Working with algebraic expressions containing fractions often involves converting improper fractions to mixed numbers for simplification.
-
Geometry: Calculating areas, volumes, and perimeters often requires working with fractions.
-
Calculus: Calculus builds upon the foundation of fractions and their manipulation.
Beyond 51/8: Practicing Fraction Conversion
To solidify your understanding, practice converting other improper fractions to mixed numbers. Try these examples:
- 23/5
- 37/6
- 49/12
- 65/9
- 82/11
By working through these examples, you'll become more proficient and confident in converting improper fractions to mixed numbers. Remember to always divide the numerator by the denominator, use the quotient as the whole number, and the remainder as the numerator of the fraction. The denominator remains the same.
Troubleshooting Common Mistakes
When converting improper fractions, some common mistakes can occur. Here are some points to watch out for:
-
Incorrect division: Double-check your division to ensure accuracy. A small error in division will lead to an incorrect mixed number.
-
Confusing the numerator and denominator: Always remember the numerator is the top number, and the denominator is the bottom number. Confusing these can lead to incorrect results.
-
Forgetting the remainder: The remainder is crucial for forming the fractional part of the mixed number. Don't forget to include it!
-
Not simplifying the fraction: Once you have your mixed number, always simplify the fractional part if possible. For example, if you end up with 6 6/12, simplify it to 6 ½.
Conclusion: Mastering Fraction Conversion
Converting 51/8 to a mixed number, as demonstrated, is a straightforward process once you grasp the fundamental concept of division and its relation to fractions. By understanding the various methods and their applications, you'll build a strong foundation in fractions, paving the way for success in more complex mathematical concepts. Remember to practice regularly and pay attention to detail to avoid common errors. With consistent effort, converting improper fractions to mixed numbers will become second nature.
Latest Posts
Latest Posts
-
Can You Have A Negative Slope
May 07, 2025
-
14 Divided By 3 With Remainder
May 07, 2025
-
Square Root Of 44 In Radical Form
May 07, 2025
-
A Comparison Of Two Quantities By Division
May 07, 2025
-
Which Pair Of Lines Are Parallel
May 07, 2025
Related Post
Thank you for visiting our website which covers about 51 8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.