60 Is 15 Percent Of What Number
News Co
May 08, 2025 · 4 min read
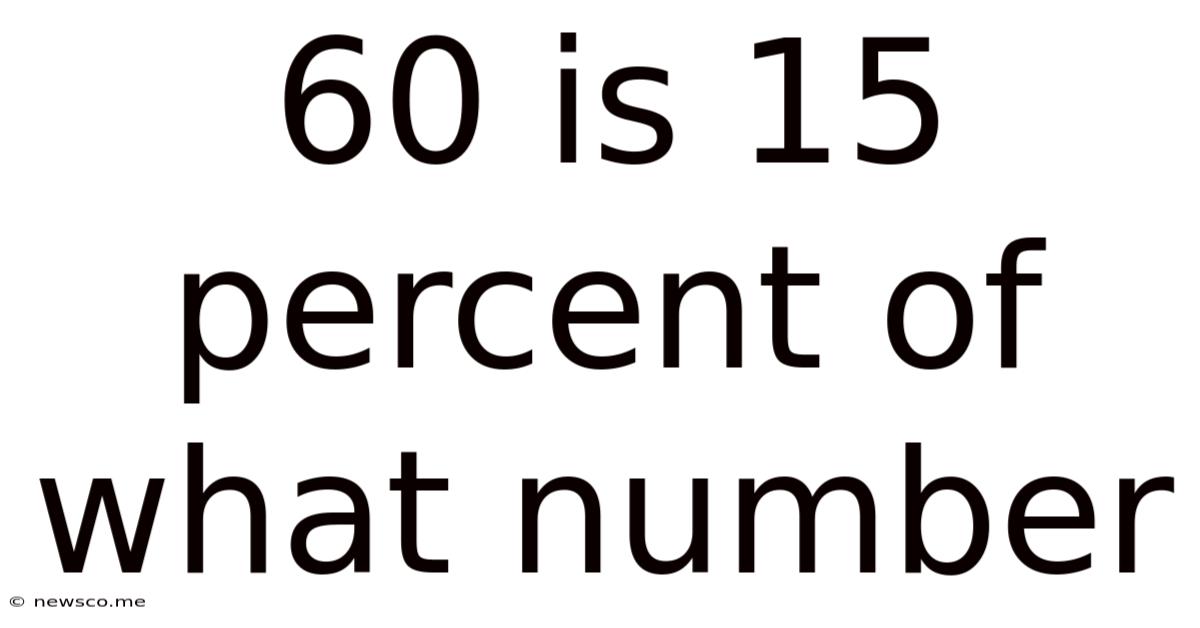
Table of Contents
60 is 15 Percent of What Number? A Comprehensive Guide to Percentage Calculations
Many everyday situations require understanding percentages. Whether you're calculating discounts, figuring out tax rates, or determining the increase in your savings, the ability to work with percentages is crucial. This article dives deep into how to solve the problem "60 is 15 percent of what number," exploring different methods, providing practical examples, and offering tips for mastering percentage calculations.
Understanding the Fundamentals of Percentages
Before we tackle the specific problem, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "percent." For example, 50% means 50 out of 100, which simplifies to 1/2 or 0.5.
Key Concepts:
- Part: This represents a portion of a whole. In our problem, 60 is the part.
- Percent: This is the rate or proportion, expressed as a percentage. In our problem, 15% is the percent.
- Whole: This is the total amount or the complete quantity. This is what we need to find.
Method 1: Using the Formula
The most common way to solve percentage problems is by using the formula:
(Part / Whole) x 100 = Percent
In our case, we know the part (60) and the percent (15%). We need to find the whole. We can rearrange the formula to solve for the whole:
Whole = (Part / Percent) x 100
Let's plug in the values:
Whole = (60 / 15) x 100
Whole = 4 x 100
Whole = 400
Therefore, 60 is 15% of 400.
Method 2: Setting up a Proportion
Another effective approach involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
60/x = 15/100
Where 'x' represents the unknown whole. To solve for x, we can cross-multiply:
60 * 100 = 15 * x
6000 = 15x
x = 6000 / 15
x = 400
This method confirms that 60 is 15% of 400.
Method 3: Using Decimal Equivalents
Percentages can easily be converted to decimals by dividing by 100. 15% is equivalent to 0.15. We can then set up the equation:
0.15 * x = 60
To solve for x, we divide both sides by 0.15:
x = 60 / 0.15
x = 400
This method again demonstrates that 60 represents 15% of 400.
Practical Applications and Real-World Examples
Understanding percentage calculations is vital in numerous real-world scenarios. Let's explore some examples:
1. Sales and Discounts:
Imagine a store offering a 15% discount on an item originally priced at $400. The discount amount would be:
0.15 * $400 = $60
The final price after the discount would be:
$400 - $60 = $340
This example directly relates to our problem, highlighting how understanding percentage calculations helps determine discounts.
2. Tax Calculations:
Suppose a sales tax rate is 15%. If the price of an item before tax is $400, the tax amount would be:
0.15 * $400 = $60
The total price including tax would be:
$400 + $60 = $460
3. Commission and Bonuses:
Salespeople often earn commission based on a percentage of their sales. If a salesperson earns a 15% commission on $4000 worth of sales, their commission would be:
0.15 * $4000 = $600
4. Interest Calculations:
Interest earned on savings accounts or loans is often calculated as a percentage of the principal amount. If you earn 15% interest on a $4000 deposit, your interest earned would be:
0.15 * $4000 = $600
Tips for Mastering Percentage Calculations
- Practice Regularly: Consistent practice is key to mastering any mathematical concept. Solve various percentage problems to build your confidence and speed.
- Understand the Formula: Thoroughly grasp the basic percentage formula and its variations.
- Use Different Methods: Experiment with different methods—formula, proportions, decimals—to find the approach that best suits your understanding.
- Check Your Work: Always double-check your calculations to ensure accuracy.
- Use a Calculator: Don't hesitate to use a calculator, especially for complex problems.
Advanced Percentage Problems and Challenges
Once you've mastered the basics, you can move on to more complex percentage problems. These might involve:
- Calculating percentage increase or decrease: This involves finding the percentage change between two values.
- Finding the original value after a percentage increase or decrease: This is the reverse of the problems we've discussed.
- Solving problems involving multiple percentages: These problems involve applying multiple percentage changes sequentially.
Conclusion: Becoming Proficient in Percentage Calculations
The ability to solve percentage problems like "60 is 15 percent of what number" is a valuable skill applicable in various aspects of life. By understanding the fundamental concepts, utilizing different calculation methods, and practicing regularly, you can confidently tackle percentage problems and apply this knowledge to real-world scenarios. Remember to always check your work and use different methods to reinforce your understanding and build your confidence. Mastering percentages will significantly enhance your numerical literacy and problem-solving capabilities.
Latest Posts
Latest Posts
-
Irrational Numbers Are Closed Under Division
May 08, 2025
-
Which Statement Is True About The Circumference Of A Circle
May 08, 2025
-
In The Following Figure The Value Of X Is
May 08, 2025
-
Chance Of Rolling A 6 With 2 Dice
May 08, 2025
-
Is 7 12 Greater Than 1 2
May 08, 2025
Related Post
Thank you for visiting our website which covers about 60 Is 15 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.