8 Is What Percent Of 8
News Co
May 07, 2025 · 4 min read
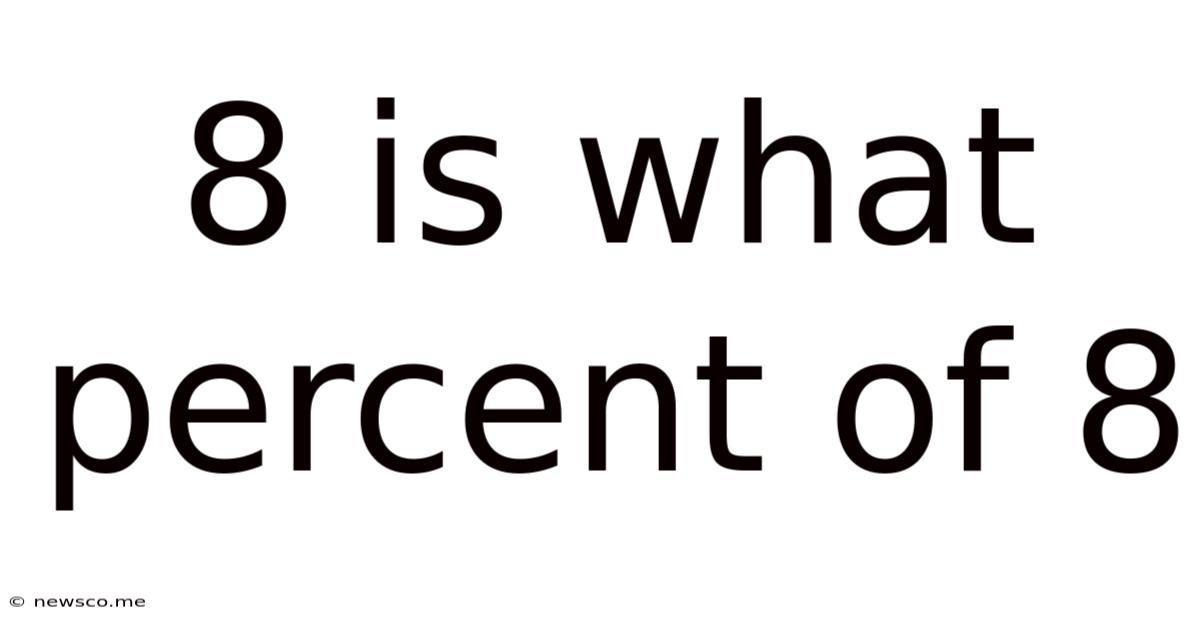
Table of Contents
8 is What Percent of 8? A Deep Dive into Percentage Calculations
This seemingly simple question, "8 is what percent of 8?", opens the door to a broader understanding of percentages, their applications, and the underlying mathematical principles. While the answer itself is straightforward, exploring the methodology and its implications provides valuable insights into a fundamental concept used across various fields. This article will not only answer the question directly but also delve into the process, offering practical examples and exploring the relevance of percentage calculations in everyday life.
Understanding Percentages: The Foundation
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred." Therefore, 10% means 10 out of 100, which can be written as the fraction 10/100 or the decimal 0.10. Understanding this fundamental principle is crucial for tackling percentage problems.
Key Concepts:
- The Whole: This represents the total amount or value you're considering. In our question, "8 is what percent of 8?", the whole is 8.
- The Part: This is the portion of the whole you're interested in. Again, in our example, the part is also 8.
- The Percentage: This expresses the part as a fraction of the whole, multiplied by 100. This is what we need to calculate.
Calculating "8 is What Percent of 8?"
The calculation itself is relatively simple. We use the following formula:
(Part / Whole) * 100 = Percentage
Substituting our values:
(8 / 8) * 100 = 100%
Therefore, 8 is 100% of 8. This makes intuitive sense; any number is 100% of itself.
Expanding the Concept: Practical Applications
While the specific example is straightforward, the underlying principle of percentage calculation is widely applicable. Let's explore some real-world scenarios:
1. Retail Discounts:
Imagine a store offering a 20% discount on an item originally priced at $80. To calculate the discount amount, we use the same percentage formula:
(20/100) * $80 = $16
The discount is $16, and the final price after the discount would be $80 - $16 = $64.
2. Grade Calculation:
A student scores 45 out of 50 on a test. To determine their percentage score:
(45 / 50) * 100 = 90%
The student achieved a 90% score on the test.
3. Financial Growth:
An investment of $1000 increases to $1200. To calculate the percentage increase:
First, find the difference: $1200 - $1000 = $200
Then, use the formula:
($200 / $1000) * 100 = 20%
The investment increased by 20%.
4. Tax Calculations:
A sales tax of 6% is applied to a purchase of $50. To calculate the tax amount:
(6/100) * $50 = $3
The sales tax is $3, and the total cost is $50 + $3 = $53.
Beyond the Basics: Advanced Percentage Applications
The simple percentage calculation extends to more complex scenarios:
1. Percentage Change:
Calculating percentage change involves determining the increase or decrease in a value over time. The formula is:
[(New Value - Old Value) / Old Value] * 100
This is crucial for tracking growth in various areas, from business profits to population statistics.
2. Compound Interest:
Compound interest involves earning interest on both the principal amount and accumulated interest. The calculation involves more complex formulas, but the underlying principle of percentage still plays a crucial role.
3. Statistical Analysis:
Percentages are extensively used in statistical analysis to represent proportions, probabilities, and trends within datasets. Understanding percentages is essential for interpreting statistical findings accurately.
Tips for Accurate Percentage Calculations
To ensure accuracy in percentage calculations, follow these guidelines:
- Identify the Whole and the Part: Clearly define which value represents the whole and which represents the part.
- Use the Correct Formula: Select the appropriate formula based on the specific problem.
- Pay Attention to Units: Ensure consistency in units throughout the calculation.
- Double-Check Your Work: Verify your calculations to avoid errors.
- Use a Calculator: For complex calculations, utilize a calculator for accuracy.
Conclusion: The Ubiquity of Percentages
The question, "8 is what percent of 8?", though seemingly simple, serves as a gateway to understanding the vast applications of percentage calculations. From everyday shopping to complex financial modeling and scientific analysis, percentages provide a crucial tool for expressing proportions and understanding change. Mastering percentage calculations is not just a mathematical skill but a valuable life skill applicable across numerous fields. The ability to confidently interpret and utilize percentages enhances decision-making and problem-solving capabilities in various aspects of life. Therefore, a thorough understanding of this fundamental concept is indispensable.
Latest Posts
Latest Posts
-
What Is The Measurement Of Angle X
May 07, 2025
-
What Is 3 1 3 As A Decimal
May 07, 2025
-
2 And 1 3 As A Improper Fraction
May 07, 2025
-
What Percent Of 500 Is 150
May 07, 2025
-
How To Find The Perimeter Of Hexagon
May 07, 2025
Related Post
Thank you for visiting our website which covers about 8 Is What Percent Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.