An Equation That States Two Ratios Are Equivalent
News Co
May 08, 2025 · 5 min read
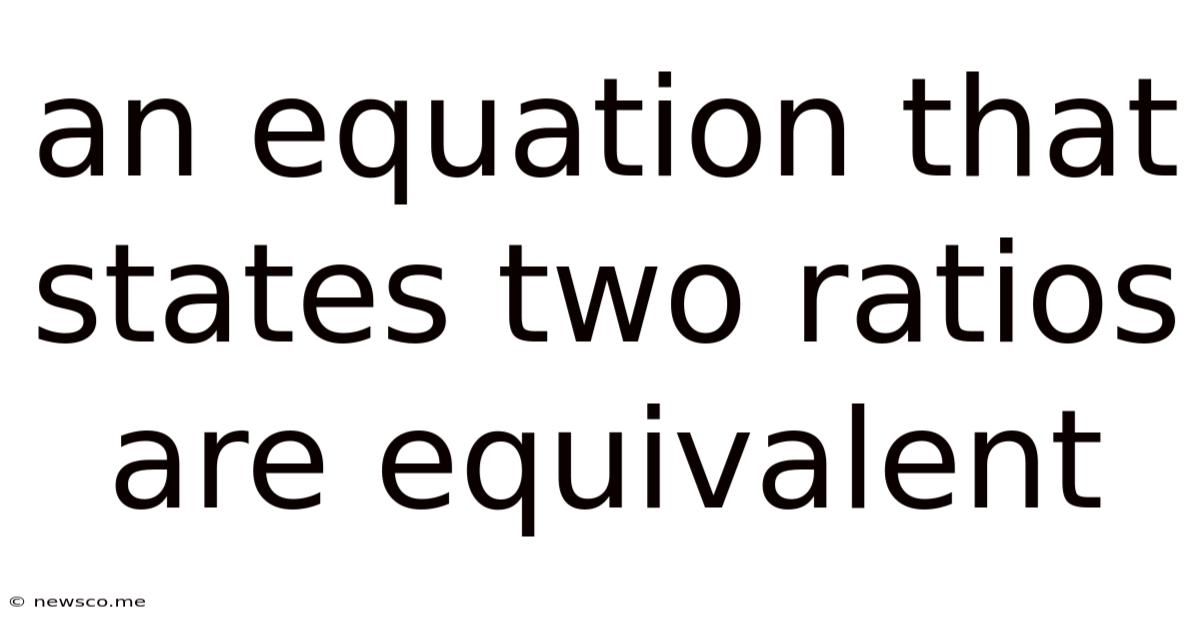
Table of Contents
An Equation That States Two Ratios Are Equivalent: Understanding Proportions
The concept of equivalent ratios, or proportions, is fundamental to mathematics and finds applications across numerous fields, from cooking and construction to finance and scientific research. Understanding what constitutes a proportion and how to manipulate proportional equations is crucial for problem-solving in various contexts. This article delves deep into the equation that states two ratios are equivalent, exploring its properties, applications, and significance in different areas of study.
What is a Ratio?
Before diving into the equation representing equivalent ratios, let's solidify our understanding of ratios themselves. A ratio is a comparison of two or more quantities. It expresses the relative size of one quantity to another. Ratios can be expressed in several ways:
- Using the colon symbol: For example, the ratio of apples to oranges is 3:5. This means for every 3 apples, there are 5 oranges.
- Using the fraction symbol: The same ratio can be represented as 3/5, indicating that the fraction of apples to the total fruit is 3/8 (assuming only apples and oranges exist).
- Using the word "to": The ratio can also be written as "3 to 5."
It's vital to understand that the order of the quantities in a ratio is significant. The ratio 3:5 is different from the ratio 5:3.
What is a Proportion?
A proportion is an equation that states that two ratios are equivalent. It expresses the equality of two ratios. The general form of a proportion is:
a/b = c/d
where 'a', 'b', 'c', and 'd' are numbers (assuming b and d are not zero to avoid division by zero), and the ratios a/b and c/d are equal. This equation essentially states that the relationship between 'a' and 'b' is the same as the relationship between 'c' and 'd'.
Understanding the Cross-Product Property
The most useful property of proportions is the cross-product property. This property states that if a/b = c/d, then:
a * d = b * c
This property provides a powerful tool for solving proportions. By cross-multiplying, we can transform a proportional equation into a simpler linear equation that can be easily solved for an unknown variable.
Applications of Proportions
Proportions are incredibly versatile and find applications in numerous areas:
1. Scaling and Resizing:
Imagine you're enlarging a photograph. If the original photograph has a width of 4 inches and a height of 6 inches, and you want to enlarge it so the width is 8 inches, you can use a proportion to find the new height:
4/6 = 8/x
Cross-multiplying gives:
4x = 48
x = 12 inches (the new height)
This same principle applies to scaling maps, blueprints, and models.
2. Unit Conversions:
Converting between different units, such as kilometers to miles or pounds to kilograms, frequently involves using proportions. For instance, if 1 kilometer is approximately equal to 0.621 miles, you can use a proportion to convert 10 kilometers to miles:
1 km / 0.621 miles = 10 km / x miles
Cross-multiplying and solving for 'x' gives the equivalent distance in miles.
3. Recipe Scaling:
Cooking often involves adjusting recipes to serve more or fewer people. Proportions are ideal for this. If a recipe calls for 2 cups of flour and 1 cup of sugar for 4 servings, and you want to make 8 servings, you can set up a proportion:
2 cups flour / 4 servings = x cups flour / 8 servings
Solving for 'x' will give you the required amount of flour for 8 servings. The same approach applies to scaling all ingredients proportionally.
4. Financial Calculations:
Proportions are commonly used in finance, for instance, in calculating interest, determining profit margins, and analyzing investment returns. For example, if an investment grows by 10% in one year, a proportion can determine the investment's value after multiple years.
5. Scientific Applications:
Proportions play a vital role in scientific experiments and data analysis. They are fundamental to understanding ratios in chemistry (e.g., molar ratios in chemical reactions), physics (e.g., calculating speeds and distances), and biology (e.g., analyzing population growth). Many scientific laws and principles can be expressed using proportional relationships.
Solving Proportions: Different Approaches
Several methods can be employed to solve proportional equations:
1. Cross-Multiplication:
As previously discussed, this is the most common and straightforward method. Cross-multiplying eliminates the fractions, resulting in a simpler equation that can be solved algebraically.
2. Finding a Common Multiplier:
If the ratios are simple enough, you can sometimes find a common multiplier to equate the two ratios. This method is useful for quick mental calculations or problems with small whole numbers.
3. Using Equivalent Fractions:
Sometimes, you might be able to simplify one or both ratios to simpler equivalent fractions. This simplification can make the comparison and solution easier.
Advanced Applications and Concepts:
1. Inverse Proportions:
While we've primarily focused on direct proportions (where an increase in one quantity leads to a proportional increase in the other), it's important to acknowledge inverse proportions. In inverse proportions, an increase in one quantity leads to a decrease in the other. The equation for an inverse proportion is:
xy = k
where 'x' and 'y' are the two quantities and 'k' is a constant.
2. Multiple Proportions:
Some problems involve more than two ratios. These situations can often be broken down into smaller proportional equations, solved individually, and then combined to find the solution.
3. Complex Ratio Problems:
Real-world applications can sometimes involve more complex ratios and proportions. These problems often require careful analysis to correctly set up the equations and solve them.
Conclusion: The Significance of Proportions
The simple equation a/b = c/d, representing the equality of two ratios, is far more powerful than it might initially appear. Understanding proportions is crucial for navigating numerous everyday situations and tackling problems across diverse scientific and practical fields. Mastering the concepts of ratios, proportions, and their applications provides a solid foundation for advanced mathematical studies and enhances problem-solving capabilities in numerous contexts. The cross-product property offers a potent tool for simplifying and solving these equations, making it an essential skill for anyone dealing with quantitative relationships. From adjusting recipes to analyzing scientific data, the versatility of proportions makes it a fundamental concept in mathematics and beyond.
Latest Posts
Latest Posts
-
What Is The Absolute Value Of 14
May 08, 2025
-
What Is 1 3 4 Divided By 2 As A Fraction
May 08, 2025
-
How Do You Write 3 As A Decimal
May 08, 2025
-
Which Of The Pairs Of Angles Are Complementary
May 08, 2025
-
How To Teach Subtraction With Regrouping 3 Digits
May 08, 2025
Related Post
Thank you for visiting our website which covers about An Equation That States Two Ratios Are Equivalent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.