Are Same Side Interior Angles Supplementary
News Co
Apr 04, 2025 · 5 min read
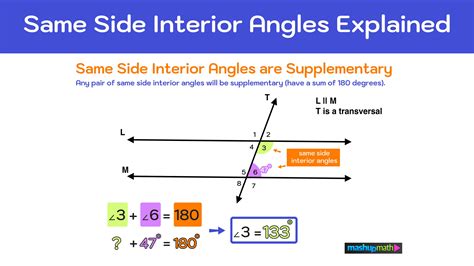
Table of Contents
Are Same-Side Interior Angles Supplementary? A Deep Dive into Parallel Lines and Transversals
Are same-side interior angles supplementary? The short answer is: yes, but only under specific conditions. This seemingly simple question opens a door to a deeper understanding of geometry, particularly the relationships between parallel lines and transversals. This comprehensive guide will explore this concept thoroughly, providing clear explanations, illustrative examples, and practical applications. We'll delve into the proofs, explore exceptions, and discuss how this concept is vital in various fields.
Understanding the Terminology
Before we dive into the core question, let's establish a strong foundation by defining key terms:
-
Parallel Lines: Two lines are parallel if they lie in the same plane and never intersect, no matter how far they are extended. We often denote parallel lines using symbols like ||. For example, line l || line m.
-
Transversal Line: A line that intersects two or more parallel lines is called a transversal. It creates various angles, which we'll explore next.
-
Interior Angles: Angles formed between the parallel lines when a transversal intersects them are called interior angles.
-
Same-Side Interior Angles: These are a pair of interior angles that lie on the same side of the transversal. They are also sometimes called consecutive interior angles.
The Supplementary Angle Theorem
The statement "same-side interior angles are supplementary" is actually a theorem, meaning it's a statement that can be proven using established geometric principles. The theorem states: If two parallel lines are cut by a transversal, then the same-side interior angles are supplementary. This means their measures add up to 180 degrees.
Proof of the Theorem
We can prove this theorem using several methods. One common approach involves using the properties of alternate interior angles and linear pairs:
-
Given: Two parallel lines, l and m, are intersected by a transversal line, t.
-
Alternate Interior Angles: We know that alternate interior angles formed by parallel lines and a transversal are congruent (equal in measure). Let's label the angles: ∠1 and ∠2 are a pair of alternate interior angles, and ∠3 and ∠4 are another pair.
-
Linear Pair: ∠2 and ∠3 form a linear pair. A linear pair consists of two adjacent angles that form a straight line, so their measures add up to 180 degrees (∠2 + ∠3 = 180°).
-
Substitution: Since ∠1 ≅ ∠2 (alternate interior angles are congruent), we can substitute ∠1 for ∠2 in the equation: ∠1 + ∠3 = 180°.
-
Conclusion: Therefore, ∠1 and ∠3 (a pair of same-side interior angles) are supplementary. The same logic can be applied to any pair of same-side interior angles formed by the parallel lines and transversal.
Illustrative Examples
Let's solidify our understanding with a couple of examples:
Example 1:
Imagine two parallel lines intersected by a transversal. One same-side interior angle measures 110 degrees. What is the measure of the other same-side interior angle?
Since same-side interior angles are supplementary, the other angle measures 180° - 110° = 70°.
Example 2:
Two parallel lines are cut by a transversal. Two same-side interior angles are represented by the algebraic expressions (2x + 10)° and (3x - 20)°. Find the value of x and the measure of each angle.
Since these angles are supplementary, their sum is 180°:
(2x + 10) + (3x - 20) = 180
5x - 10 = 180
5x = 190
x = 38
Now substitute x = 38 back into the expressions:
(2 * 38 + 10)° = 86°
(3 * 38 - 20)° = 94°
The two angles measure 86° and 94°, and their sum is indeed 180°.
Converse of the Theorem
The converse of a theorem is formed by switching the hypothesis and the conclusion. The converse of the same-side interior angles theorem is: If two lines are cut by a transversal such that same-side interior angles are supplementary, then the two lines are parallel.
This converse is also true and can be proven using similar geometric principles. This bidirectional relationship is crucial in various applications.
Applications in Real Life and Other Fields
The concept of same-side interior angles and their supplementary nature has far-reaching applications:
-
Construction and Engineering: Architects and engineers utilize these principles when designing parallel structures, ensuring stability and accuracy. For instance, ensuring the parallel alignment of beams or walls in a building.
-
Computer Graphics: In computer-aided design (CAD) and other computer graphics applications, the relationships between parallel lines and transversals are fundamental for creating accurate and realistic representations of objects and scenes.
-
Navigation: Understanding angular relationships between lines helps in navigation, such as determining bearings and directions using maps and compasses.
-
Surveying: Surveyors use these geometric principles to determine distances and angles in land measurement and mapping.
-
Game Development: In game development, understanding these principles is crucial for creating realistic physics engines and accurate rendering of 3D environments.
Exceptions and Important Considerations
While the theorem holds true for parallel lines, it's crucial to understand that if the lines are not parallel, the same-side interior angles will not be supplementary. Their sum will be different from 180 degrees. This is a key distinction.
Advanced Concepts and Extensions
For those seeking a more in-depth understanding, exploring these advanced topics can be beneficial:
-
Proving the converse of the theorem: This provides a deeper understanding of the bi-directional relationship between parallel lines and supplementary same-side interior angles.
-
Exploring other angle relationships formed by transversals: Investigating alternate interior angles, alternate exterior angles, and corresponding angles further solidifies the understanding of parallel lines and their interactions.
-
Applications in non-Euclidean geometry: Investigating how these concepts might differ in geometries beyond the Euclidean system.
Conclusion
The question "Are same-side interior angles supplementary?" leads to a rich exploration of geometric principles. While the answer is a resounding "yes" under the condition that the lines are parallel, understanding the underlying theorem, its proof, and its converse is vital. The applications of this fundamental concept extend far beyond the classroom, playing a crucial role in various fields demanding precision and accuracy. By mastering this concept, you are not only enhancing your geometric knowledge but also acquiring tools applicable in numerous real-world situations. Remember, understanding the conditions under which the theorem holds true is just as important as understanding the theorem itself.
Latest Posts
Latest Posts
-
Which Is Bigger 7 8 Or 3 4
Apr 05, 2025
-
Having A Set Of 2 Coordinates
Apr 05, 2025
-
Decimal Place Value Worksheets Grade 5
Apr 05, 2025
-
How Long Is 48 Weeks In Months
Apr 05, 2025
-
Formula For Standard Deviation Of Grouped Data
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Are Same Side Interior Angles Supplementary . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
