Gcf Of 10 15 And 30
News Co
May 04, 2025 · 5 min read
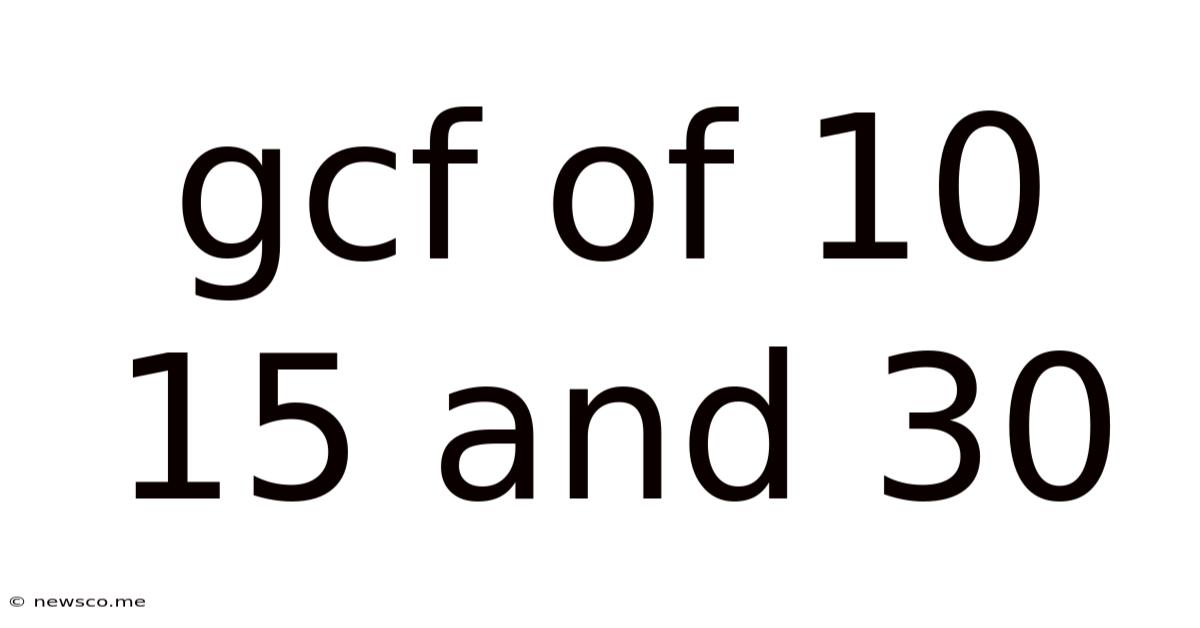
Table of Contents
Finding the Greatest Common Factor (GCF) of 10, 15, and 30: A Comprehensive Guide
Determining the Greatest Common Factor (GCF), also known as the Greatest Common Divisor (GCD), of a set of numbers is a fundamental concept in mathematics with wide-ranging applications. This article delves deep into the process of finding the GCF of 10, 15, and 30, exploring multiple methods and illustrating the underlying principles. We'll move beyond a simple answer and unpack the theory behind GCF calculation, providing a robust understanding that extends to more complex scenarios.
Understanding the Greatest Common Factor (GCF)
The GCF of a set of numbers is the largest number that divides each of the numbers in the set without leaving a remainder. In simpler terms, it's the biggest number that fits perfectly into all the numbers you're considering. For example, if we consider the numbers 12 and 18, their common factors are 1, 2, 3, and 6. The greatest among these is 6, making 6 the GCF of 12 and 18.
Understanding the concept of factors is crucial. Factors are whole numbers that divide another number evenly. For instance, the factors of 10 are 1, 2, 5, and 10. The factors of 15 are 1, 3, 5, and 15. And the factors of 30 are 1, 2, 3, 5, 6, 10, 15, and 30.
Method 1: Listing Factors
This method, while straightforward for smaller numbers like 10, 15, and 30, can become cumbersome with larger numbers. Let's illustrate:
-
List the factors of 10: 1, 2, 5, 10
-
List the factors of 15: 1, 3, 5, 15
-
List the factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
-
Identify common factors: Observe the factors that appear in all three lists. These are 1 and 5.
-
Determine the GCF: The largest common factor is 5. Therefore, the GCF of 10, 15, and 30 is 5.
This method relies on meticulous listing and comparison, making it less efficient for larger numbers or a greater number of inputs.
Method 2: Prime Factorization
Prime factorization is a more systematic and scalable approach, particularly useful when dealing with larger numbers. This method involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Prime factorize 10: 10 = 2 x 5
-
Prime factorize 15: 15 = 3 x 5
-
Prime factorize 30: 30 = 2 x 3 x 5
-
Identify common prime factors: Notice that the number 5 appears in all three prime factorizations.
-
Calculate the GCF: The GCF is the product of the common prime factors. In this case, the GCF is simply 5.
Prime factorization provides a clear and organized method, making it easier to handle larger numbers and identify the GCF effectively. The process is more efficient than listing all factors, particularly for numbers with multiple factors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers. It can be extended to find the GCF of more than two numbers by applying it iteratively.
Let's illustrate with 10, 15, and 30. We'll apply the Euclidean algorithm iteratively:
-
Find the GCF of 10 and 15:
- Divide 15 by 10: 15 = 10 x 1 + 5
- The remainder is 5. Now, consider the divisor (10) and the remainder (5).
- Divide 10 by 5: 10 = 5 x 2 + 0
- The remainder is 0. The GCF of 10 and 15 is the last non-zero remainder, which is 5.
-
Find the GCF of the result (5) and the next number (30):
- Divide 30 by 5: 30 = 5 x 6 + 0
- The remainder is 0. The GCF of 5 and 30 is 5.
Therefore, the GCF of 10, 15, and 30 is 5.
The Euclidean algorithm is particularly efficient for large numbers because it avoids the need to list all factors. It's a powerful tool for computational applications where GCF calculation is a frequent operation.
Applications of GCF
The concept of GCF has far-reaching applications across various mathematical fields and practical scenarios:
-
Simplifying Fractions: Finding the GCF allows us to simplify fractions to their lowest terms. For example, the fraction 30/15 can be simplified by dividing both the numerator and denominator by their GCF (5), resulting in the equivalent fraction 6/3, which further simplifies to 2/1 or 2.
-
Solving Word Problems: Many word problems involving sharing or dividing objects equally rely on the GCF to find the largest equal groups that can be formed. For instance, if you have 30 apples and 15 oranges, the GCF helps determine the largest number of identical fruit baskets you can create.
-
Geometry and Measurement: GCF plays a crucial role in problems related to area, perimeter, and volume calculations, particularly when dealing with rectangular shapes or objects with dimensions that need to be simplified.
-
Number Theory: GCF is a fundamental concept in number theory, forming the basis for more advanced topics like modular arithmetic and cryptography.
-
Computer Science: Algorithms like the Euclidean algorithm are employed extensively in computer science for various applications, including cryptography and data compression.
Extending the Concept: More than Three Numbers
The methods described above can be extended to find the GCF of more than three numbers. For the prime factorization method, you would simply factorize all the numbers and find the common prime factors. For the Euclidean algorithm, you would iteratively find the GCF of two numbers at a time, continuing until you find the GCF of all the numbers.
Conclusion: Mastering GCF Calculations
Finding the GCF of a set of numbers is a cornerstone of mathematical understanding. While simple for smaller numbers, mastering efficient methods like prime factorization and the Euclidean algorithm is crucial for tackling larger numbers and complex problems. Understanding the underlying principles and the various methods empowers you to confidently approach GCF calculations in various mathematical contexts and real-world applications. This comprehensive guide provides a solid foundation for understanding and applying this fundamental concept. Remember to choose the method that best suits the complexity of the numbers involved – listing factors is suitable for smaller numbers, while prime factorization and the Euclidean algorithm are more efficient for larger numbers.
Latest Posts
Latest Posts
-
Are 46 And 105 Relatively Prime
May 04, 2025
-
Are Same Side Exterior Angles Congruent Or Supplementary
May 04, 2025
-
What Fraction Is Represented By Point A
May 04, 2025
-
Difference Between F Test And T Test
May 04, 2025
-
How To Find The General Term Of A Sequence
May 04, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 10 15 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.