Gcf Of 16 24 And 40
News Co
May 07, 2025 · 6 min read
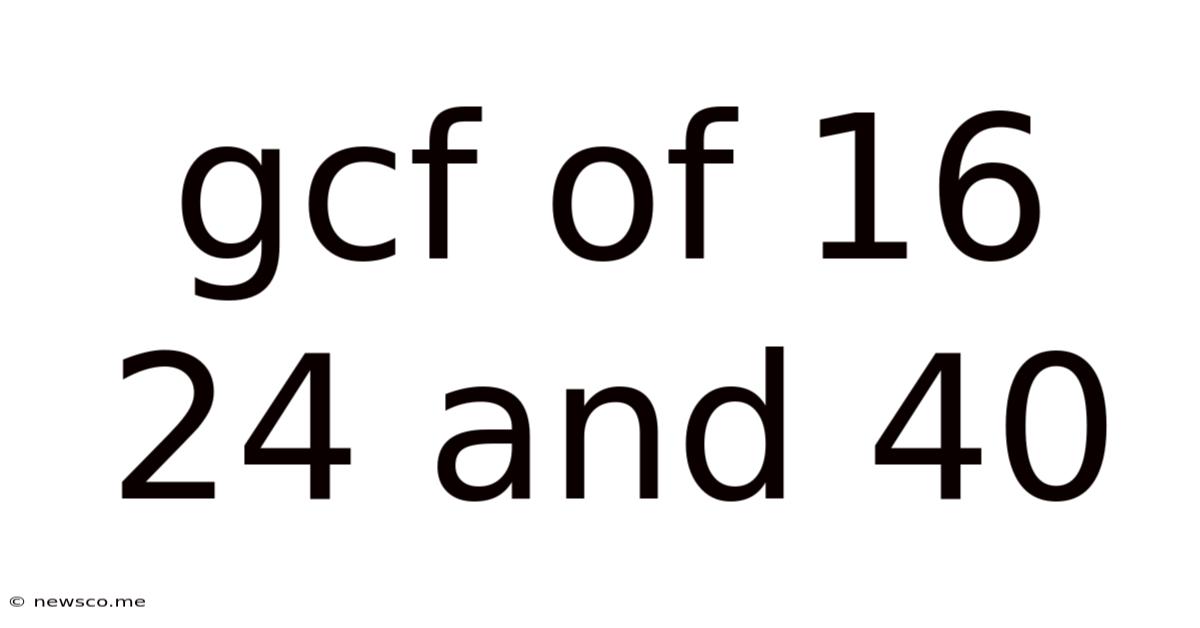
Table of Contents
Finding the Greatest Common Factor (GCF) of 16, 24, and 40: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of a set of numbers is a fundamental concept in mathematics with applications spanning various fields, from simplifying fractions to solving complex algebraic equations. This article delves into the process of determining the GCF of 16, 24, and 40, exploring multiple methods and providing a thorough understanding of the underlying principles. We'll also touch upon the practical applications of finding the GCF and discuss related mathematical concepts.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. It's a crucial concept in simplifying fractions, factoring polynomials, and solving various mathematical problems. Think of it as the largest shared building block of the numbers.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. Therefore, the greatest common factor (GCF) of 12 and 18 is 6.
Methods for Finding the GCF of 16, 24, and 40
Several methods can be employed to find the GCF of 16, 24, and 40. Let's explore the most common ones:
1. Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest factor common to all.
- Factors of 16: 1, 2, 4, 8, 16
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
Comparing the lists, we see that the common factors are 1, 2, 4, and 8. The greatest of these common factors is 8. Therefore, the GCF of 16, 24, and 40 is 8.
This method is straightforward for smaller numbers, but it becomes cumbersome and inefficient when dealing with larger numbers or a greater number of numbers.
2. Prime Factorization Method
This method involves expressing each number as a product of its prime factors. The prime factorization of a number is a unique representation of that number as a product of only prime numbers (numbers greater than 1 that are only divisible by 1 and themselves).
- Prime factorization of 16: 2 x 2 x 2 x 2 = 2⁴
- Prime factorization of 24: 2 x 2 x 2 x 3 = 2³ x 3
- Prime factorization of 40: 2 x 2 x 2 x 5 = 2³ x 5
Once you have the prime factorization of each number, identify the common prime factors and their lowest powers. In this case, the only common prime factor is 2, and its lowest power is 2³. Therefore, the GCF is 2³ = 8.
This method is generally more efficient than listing factors, especially for larger numbers. It provides a structured and systematic approach to finding the GCF.
3. Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF of two numbers. It can be extended to find the GCF of more than two numbers by applying the algorithm repeatedly.
To find the GCF of 16, 24, and 40 using the Euclidean algorithm, we first find the GCF of two of the numbers, say 16 and 24.
- Divide the larger number (24) by the smaller number (16): 24 ÷ 16 = 1 with a remainder of 8.
- Replace the larger number with the smaller number (16) and the smaller number with the remainder (8): Now we find the GCF of 16 and 8.
- Divide 16 by 8: 16 ÷ 8 = 2 with a remainder of 0.
- Since the remainder is 0, the GCF of 16 and 24 is 8.
Now we find the GCF of this result (8) and the remaining number (40).
- Divide 40 by 8: 40 ÷ 8 = 5 with a remainder of 0.
- Since the remainder is 0, the GCF of 8 and 40 is 8.
Therefore, the GCF of 16, 24, and 40 is 8.
The Euclidean algorithm is particularly efficient for larger numbers as it avoids the need to find all factors.
Applications of Finding the GCF
The concept of the greatest common factor has numerous practical applications in various areas of mathematics and beyond:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 24/40 can be simplified by dividing both the numerator and the denominator by their GCF, which is 8. This simplifies the fraction to 3/5.
-
Factoring Polynomials: Finding the GCF of the terms in a polynomial allows you to factor out the common factor, simplifying the polynomial and making it easier to solve equations.
-
Solving Linear Diophantine Equations: The Euclidean algorithm, used to find the GCF, is crucial in solving linear Diophantine equations, which are equations involving only integer variables.
-
Number Theory: The GCF plays a fundamental role in various concepts in number theory, such as modular arithmetic and cryptography.
-
Real-World Applications: GCF concepts are applied in various practical scenarios, including dividing objects into equal groups, determining the largest possible size of square tiles to cover a rectangular area, and scheduling tasks with overlapping time constraints.
Extending the Concept: Least Common Multiple (LCM)
Closely related to the GCF is the least common multiple (LCM). The LCM of two or more numbers is the smallest number that is a multiple of all the given numbers.
The relationship between the GCF and LCM is given by the formula:
LCM(a, b) x GCF(a, b) = a x b
For example, using the numbers 16, 24, and 40, we've found the GCF to be 8. To find the LCM of 16, 24, and 40, we can use the prime factorization method:
- Prime factorization of 16: 2⁴
- Prime factorization of 24: 2³ x 3
- Prime factorization of 40: 2³ x 5
The LCM is found by taking the highest power of each prime factor present in the numbers: 2⁴ x 3 x 5 = 240. Therefore, the LCM of 16, 24, and 40 is 240.
Conclusion
Finding the greatest common factor (GCF) is a vital skill in mathematics with applications extending far beyond the classroom. This article has explored various methods for determining the GCF of 16, 24, and 40, highlighting the advantages and disadvantages of each approach. Understanding the concept of GCF and its relationship to the least common multiple (LCM) is essential for mastering numerous mathematical concepts and solving real-world problems. By utilizing the methods described here, you can confidently tackle GCF problems of any complexity. Remember to choose the method best suited to the numbers involved for efficiency and accuracy.
Latest Posts
Latest Posts
-
Can You Have A Negative Slope
May 07, 2025
-
14 Divided By 3 With Remainder
May 07, 2025
-
Square Root Of 44 In Radical Form
May 07, 2025
-
A Comparison Of Two Quantities By Division
May 07, 2025
-
Which Pair Of Lines Are Parallel
May 07, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 16 24 And 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.