Graphing Quadratic Functions Worksheet With Answers Pdf
News Co
Apr 03, 2025 · 6 min read
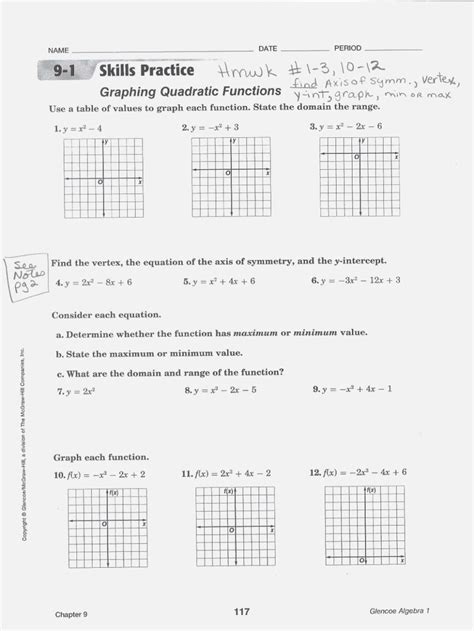
Table of Contents
Graphing Quadratic Functions Worksheet with Answers: A Comprehensive Guide
This comprehensive guide provides a detailed explanation of graphing quadratic functions, accompanied by a sample worksheet with answers. Understanding quadratic functions is crucial for success in algebra and beyond, forming the foundation for more advanced mathematical concepts. This guide aims to equip you with the knowledge and skills to confidently graph these functions and interpret their characteristics.
Understanding Quadratic Functions
A quadratic function is a polynomial function of degree two, meaning the highest power of the variable (usually x) is 2. It's generally represented in the standard form:
f(x) = ax² + bx + c
where a, b, and c are constants, and a ≠ 0 (if a were 0, it wouldn't be a quadratic function). The graph of a quadratic function is a parabola, a U-shaped curve that opens either upwards (if a > 0) or downwards (if a < 0).
Key Features of a Parabola
Several key features help us understand and graph a parabola:
-
Vertex: The vertex is the turning point of the parabola. It's either the lowest point (minimum) if the parabola opens upwards or the highest point (maximum) if it opens downwards. The x-coordinate of the vertex can be found using the formula: x = -b / 2a. Substituting this x-value back into the quadratic equation gives the y-coordinate of the vertex.
-
Axis of Symmetry: This is a vertical line that passes through the vertex, dividing the parabola into two symmetrical halves. Its equation is simply x = -b / 2a, the same as the x-coordinate of the vertex.
-
x-intercepts (Roots or Zeros): These are the points where the parabola intersects the x-axis (where y = 0). They can be found by solving the quadratic equation ax² + bx + c = 0. This can be done using factoring, the quadratic formula, or completing the square.
-
y-intercept: This is the point where the parabola intersects the y-axis (where x = 0). It's simply the value of c in the standard form of the quadratic equation, i.e., (0, c).
Methods for Graphing Quadratic Functions
There are several ways to graph a quadratic function:
1. Using the Vertex Form
The vertex form of a quadratic function provides a straightforward method for graphing:
f(x) = a(x - h)² + k
where (h, k) represents the coordinates of the vertex. The value of 'a' determines the parabola's direction and vertical stretch or compression.
Example: f(x) = 2(x - 3)² + 1
The vertex is (3, 1). Since a = 2 > 0, the parabola opens upwards. We can then plot the vertex and a few other points by substituting x-values into the equation to find their corresponding y-values. The axis of symmetry is x = 3.
2. Using the Standard Form and Key Features
Graphing using the standard form (f(x) = ax² + bx + c) involves finding the vertex, axis of symmetry, x-intercepts, and y-intercept.
Steps:
- Find the vertex: Use the formula x = -b / 2a to find the x-coordinate, and then substitute this value back into the equation to find the y-coordinate.
- Find the axis of symmetry: This is the vertical line x = -b / 2a.
- Find the y-intercept: This is the point (0, c).
- Find the x-intercepts (if any): Solve the quadratic equation ax² + bx + c = 0 using factoring, the quadratic formula, or completing the square.
- Plot the points and sketch the parabola: Plot the vertex, axis of symmetry, y-intercept, and x-intercepts (if they exist). Remember that the parabola is symmetrical around the axis of symmetry, so you can use this to plot additional points if needed.
3. Using a Table of Values
This method involves creating a table of x and y values. Choose several x-values, substitute them into the quadratic equation to find the corresponding y-values, and then plot these points on the coordinate plane to sketch the parabola. This method is particularly useful when dealing with more complex quadratic equations.
Sample Worksheet with Answers
Here’s a sample worksheet to practice graphing quadratic functions. Remember to show your work to fully understand the process.
(Worksheet)
Graph the following quadratic functions. Identify the vertex, axis of symmetry, x-intercepts (if any), and y-intercept for each.
- f(x) = x² + 4x + 3
- f(x) = -x² + 2x + 8
- f(x) = 2x² - 8x + 6
- f(x) = (x - 1)² - 4
- f(x) = - (x + 2)² + 9
(Answers)
Note: The following answers provide the key features. The actual graphing requires plotting these points on a coordinate plane and sketching the parabola.
-
f(x) = x² + 4x + 3
- Vertex: (-2, -1)
- Axis of Symmetry: x = -2
- x-intercepts: (-3, 0), (-1, 0)
- y-intercept: (0, 3)
-
f(x) = -x² + 2x + 8
- Vertex: (1, 9)
- Axis of Symmetry: x = 1
- x-intercepts: (-2, 0), (4, 0)
- y-intercept: (0, 8)
-
f(x) = 2x² - 8x + 6
- Vertex: (2, -2)
- Axis of Symmetry: x = 2
- x-intercepts: (1, 0), (3, 0)
- y-intercept: (0, 6)
-
f(x) = (x - 1)² - 4 (Vertex form)
- Vertex: (1, -4)
- Axis of Symmetry: x = 1
- x-intercepts: (-1, 0), (3, 0)
- y-intercept: (0, -3)
-
f(x) = - (x + 2)² + 9 (Vertex form)
- Vertex: (-2, 9)
- Axis of Symmetry: x = -2
- x-intercepts: (-5, 0), (1, 0)
- y-intercept: (0, 5)
Advanced Concepts and Applications
Understanding quadratic functions extends beyond basic graphing. More advanced concepts include:
-
Completing the Square: This algebraic technique is used to rewrite a quadratic function in vertex form, making it easier to identify the vertex and graph the function.
-
The Discriminant: The discriminant (b² - 4ac) from the quadratic formula helps determine the number and nature of the x-intercepts. If the discriminant is positive, there are two distinct real roots (x-intercepts). If it's zero, there's one real root (the vertex touches the x-axis). If it's negative, there are no real roots (the parabola doesn't intersect the x-axis).
-
Maximum and Minimum Values: The y-coordinate of the vertex represents the maximum or minimum value of the quadratic function. This is crucial in optimization problems, where we need to find the maximum or minimum value of a quantity.
-
Modeling Real-World Situations: Quadratic functions are used to model various real-world phenomena, such as projectile motion, the shape of a satellite dish, and the path of a ball thrown in the air.
By mastering the concepts and techniques outlined in this guide and practicing with numerous examples, you'll develop a strong understanding of graphing quadratic functions, opening doors to more advanced mathematical explorations and real-world applications. Remember that consistent practice is key to success in mastering this essential algebraic topic.
Latest Posts
Latest Posts
-
How Long Is 7 Months In Weeks
Apr 04, 2025
-
Greatest Common Factor For 12 And 16
Apr 04, 2025
-
What Is The Gcf Of 26 And 34
Apr 04, 2025
-
Is 30 A Prime Or Composite Number
Apr 04, 2025
-
How To Compute 90 Confidence Interval
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Graphing Quadratic Functions Worksheet With Answers Pdf . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
