How Do You Find The Volume Of A Pentagonal Prism
News Co
Mar 30, 2025 · 6 min read
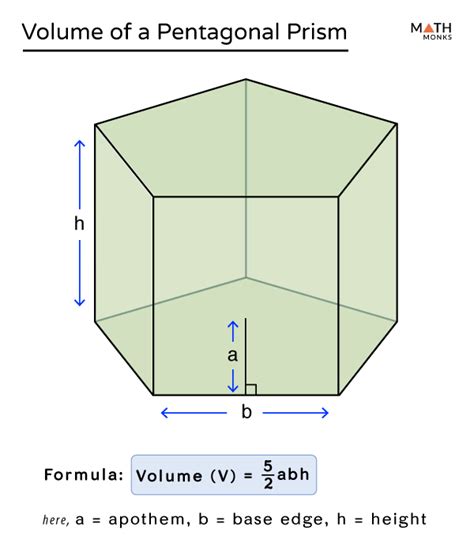
Table of Contents
How to Find the Volume of a Pentagonal Prism: A Comprehensive Guide
Determining the volume of a three-dimensional shape is a fundamental concept in geometry with wide-ranging applications in various fields, from architecture and engineering to physics and computer graphics. This comprehensive guide will delve into the intricacies of calculating the volume of a pentagonal prism, a geometric solid with a pentagon as its base. We will explore different approaches, provide step-by-step instructions, and offer practical examples to solidify your understanding.
Understanding Pentagonal Prisms
Before diving into the calculations, let's clearly define what a pentagonal prism is. A pentagonal prism is a three-dimensional geometric shape composed of two parallel congruent pentagonal bases connected by five rectangular lateral faces. Imagine a regular pentagon (a five-sided polygon with all sides and angles equal) extended into a three-dimensional shape. That's essentially a pentagonal prism.
The base of the prism is the pentagon, and the height of the prism is the perpendicular distance between the two parallel pentagonal bases. Understanding these fundamental components is crucial for calculating the volume.
Key Formulas and Concepts
The volume of any prism, including a pentagonal prism, is calculated using a straightforward formula:
Volume = Base Area × Height
This means that to find the volume, we need to determine the area of the pentagonal base and multiply it by the prism's height. This seemingly simple formula masks a slightly more complex process when dealing with pentagons, as calculating the area of a pentagon requires further steps.
Calculating the Area of a Regular Pentagon
Let's assume, for simplicity, that our pentagonal prism has a regular pentagon as its base. A regular pentagon has all five sides of equal length and all five interior angles equal (108 degrees each). There are several methods to calculate the area of a regular pentagon, each with its own advantages:
Method 1: Using the Apothem
The apothem of a regular polygon is the distance from the center of the polygon to the midpoint of any side. If we know the apothem (a) and the side length (s) of the regular pentagon, we can use the following formula:
Area = (1/2) × Perimeter × Apothem = (1/2) × (5s) × a
Where:
- s is the length of one side of the pentagon.
- a is the apothem of the pentagon.
This method is efficient if the apothem is readily available or easily calculated.
Method 2: Using the Side Length
If only the side length (s) of the regular pentagon is known, we can utilize trigonometry to calculate its area. The formula is derived from dividing the pentagon into five congruent triangles and using the properties of these triangles.
Area = (1/4)√(5(5+2√5)) × s²
This formula directly relates the area to the side length, making it convenient when the apothem is unknown.
Method 3: Dividing into Triangles
This method involves dividing the pentagon into five congruent isosceles triangles. By finding the area of one triangle and multiplying by five, we obtain the area of the pentagon. This requires knowledge of the side length and the use of trigonometric functions to calculate the height of each triangle.
This approach is useful for demonstrating the underlying geometry but is computationally more involved than the previous two methods.
Calculating the Volume of a Pentagonal Prism: Step-by-Step
Now, let's put it all together. To calculate the volume of a pentagonal prism, follow these steps:
-
Identify the type of pentagon: Determine if the base is a regular or irregular pentagon. The methods for calculating the base area differ depending on this.
-
Measure the necessary parameters: For a regular pentagon, you need either the side length (s) and the apothem (a) or just the side length (s). For an irregular pentagon, you'll need to break it down into smaller shapes (triangles, etc.) and find their areas individually. Measure the height (h) of the prism.
-
Calculate the base area: Use one of the methods described above (Method 1, 2, or 3) to calculate the area (A) of the pentagonal base. If it's an irregular pentagon, the process will be more complex and may involve dividing the pentagon into smaller, more manageable shapes.
-
Calculate the volume: Once you have the base area (A) and the height (h) of the prism, apply the fundamental formula:
Volume = A × h
-
State the units: Remember to include the appropriate units (cubic centimeters, cubic meters, cubic inches, etc.) in your final answer.
Examples
Let's illustrate the process with a few examples:
Example 1: Regular Pentagon
A regular pentagonal prism has a base with a side length of 5 cm and an apothem of 3.44 cm. The height of the prism is 10 cm.
-
Base Area: Using Method 1: Area = (1/2) × (5 × 5 cm) × 3.44 cm = 43 cm²
-
Volume: Volume = 43 cm² × 10 cm = 430 cm³
Example 2: Regular Pentagon (using side length only)
A regular pentagonal prism has a base with a side length of 8 cm and a height of 12 cm.
-
Base Area: Using Method 2: Area = (1/4)√(5(5+2√5)) × (8 cm)² ≈ 110 cm²
-
Volume: Volume = 110 cm² × 12 cm = 1320 cm³
Example 3: Irregular Pentagon (approximation)
An irregular pentagonal prism has a base that can be approximated as the sum of a rectangle (4 cm x 6 cm) and a right-angled triangle (base 4 cm, height 3 cm). The prism height is 7 cm.
-
Base Area: Area of Rectangle = 4 cm × 6 cm = 24 cm²; Area of Triangle = (1/2) × 4 cm × 3 cm = 6 cm²; Total Base Area = 24 cm² + 6 cm² = 30 cm²
-
Volume: Volume = 30 cm² × 7 cm = 210 cm³
Advanced Concepts and Applications
The calculation of pentagonal prism volume extends beyond simple geometric problems. It finds applications in various fields:
-
Architecture and Engineering: Calculating the volume of materials needed for construction projects involving pentagonal structures.
-
Civil Engineering: Determining the volume of earthworks or excavations involving pentagonal cross-sections.
-
Computer Graphics and 3D Modeling: Precise volume calculation is essential for realistic rendering and simulations in computer-aided design (CAD) software.
Conclusion
Mastering the calculation of the volume of a pentagonal prism is an important skill in geometry. By understanding the different methods for determining the area of a pentagon and applying the fundamental volume formula, you can confidently tackle various problems involving this three-dimensional shape. Remember to choose the appropriate method based on the available information and always double-check your calculations to ensure accuracy. The examples provided offer a practical guide, and further exploration into related geometric concepts will strengthen your understanding and problem-solving abilities.
Latest Posts
Latest Posts
-
What Is 0 4 Repeating As A Fraction
Apr 01, 2025
-
First Derivative Test And Second Derivative Test
Apr 01, 2025
-
How To Find Equation Of A Vertical Line
Apr 01, 2025
-
Is 37 A Prime Number Or A Composite Number
Apr 01, 2025
-
What Can 19 Be Divided By
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How Do You Find The Volume Of A Pentagonal Prism . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
