How To Convert A Mixed Fraction To A Whole Number
News Co
Apr 03, 2025 · 6 min read
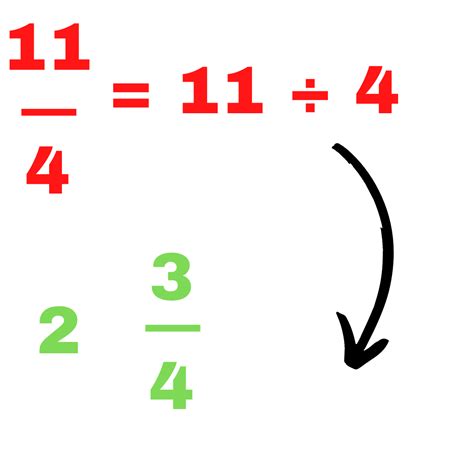
Table of Contents
How to Convert a Mixed Fraction to a Whole Number (It's Easier Than You Think!)
Mixed fractions, those numbers that combine a whole number and a fraction (like 2 ¾), can sometimes seem intimidating. But converting them to whole numbers isn't as complex as it might first appear. While a direct conversion isn't always possible (since mixed fractions inherently contain a fractional part), we can explore several approaches depending on what you need to achieve. This comprehensive guide will explore various methods, tackling common misconceptions and providing clear, step-by-step instructions.
Understanding Mixed Fractions and Whole Numbers
Before diving into the conversion process, let's briefly revisit the definitions:
-
Mixed Fraction: A number consisting of a whole number and a proper fraction. A proper fraction is a fraction where the numerator (top number) is smaller than the denominator (bottom number). Examples include 3 ½, 1 ¹/₆, and 10 ⅘.
-
Whole Number: A number without any fractional or decimal part. These are non-negative numbers, including zero (0, 1, 2, 3, and so on).
The key takeaway is that you cannot directly convert a mixed fraction into a whole number and preserve its exact value. The fractional component needs to be addressed. The methods below will explore how to handle this fractional component to arrive at a whole number approximation or a related whole number representation.
Method 1: Rounding to the Nearest Whole Number
This is the simplest approach and is suitable when you only need an approximate whole number value. Rounding involves determining whether the fractional part is closer to 0 or 1.
Steps:
-
Identify the fractional part: Look at the fraction in your mixed number. For example, in 2 ¾, the fractional part is ¾.
-
Determine if the fraction is closer to 0 or 1: If the numerator is less than half the denominator, round down to 0. If the numerator is greater than or equal to half the denominator, round up to 1. In our example, ¾ is closer to 1 than 0.
-
Add the rounded fraction to the whole number: Add the rounded value (0 or 1) to the whole number part of the mixed fraction. So, 2 ¾ rounds up to 3.
Examples:
- 1 ¹/₆ rounds down to 1 (because ¹/₆ is less than ½).
- 5 ⅔ rounds up to 6 (because ⅔ is greater than ½).
- 10 ⅘ rounds up to 11 (because ⅘ is greater than ½).
When to use this method: This method is useful for estimations, quick calculations, or situations where a precise value isn't crucial.
Method 2: Rounding Up or Down (Depending on the Context)
Sometimes, the context of the problem dictates whether you round up or down, even if the fraction isn't exactly halfway. This might involve practical considerations like needing extra material, or being safe rather than sorry.
Examples:
-
Scenario: You need to buy enough paint to cover a wall that requires 3 ½ gallons of paint. You can't buy half gallons.
- Solution: You'd round up to 4 gallons to ensure you have enough paint.
-
Scenario: You have 5 ⅛ meters of fabric, and you need 5 meters for a project.
- Solution: You could round down to 5 meters (but this is risky, as the ⅛ might create a problem).
This method emphasizes practical application over strict mathematical precision.
Method 3: Converting to an Improper Fraction then to a Whole Number (Approximation)
This method provides a more precise approach than simply rounding. It involves converting the mixed fraction into an improper fraction, and then determining if it can be approximated to a whole number. This is only possible if the fractional part is sufficiently small.
Steps:
-
Convert the mixed fraction to an improper fraction: Multiply the whole number by the denominator, add the numerator, and keep the same denominator. For 2 ¾, this becomes (2 * 4) + 3 = 11, so the improper fraction is 11/4.
-
Determine if the improper fraction can be reasonably approximated to a whole number: The closer the improper fraction is to a whole number, the better the approximation. For example, 11/4 is close to 3.
-
If applicable, assign the nearest whole number: If the improper fraction can be reasonably approximated to a whole number, then this whole number can be assigned. Otherwise, the method is not applicable and you might need to use other methods.
Examples:
- 2 ¾ (11/4) ≈ 3 (a reasonable approximation)
- 1 ¹/₆ (7/6) ≈ 1 (a reasonable approximation, slightly above 1)
- 5 ⁹⁹/₁₀₀ (599/100) ≈ 6 (a reasonable approximation)
When to use this method: Use this when you need a closer approximation than simple rounding offers, but a strict conversion isn't necessary.
Method 4: Finding the Closest Whole Number Multiple
This technique involves identifying the closest whole number that is a multiple of the denominator of the fraction.
Steps:
-
Look at the denominator of the fraction: In 2 ¾, the denominator is 4.
-
Find multiples of the denominator: Find the closest multiples of 4 (like 4, 8, 12, etc.)
-
See what whole number this corresponds to: The closest to 2 ¾ is 3 (which corresponds to 12/4).
When to Use: This is best for situations where you need a reasonable whole number representation, considering the denominator's influence.
Method 5: Using the Fractional Part for Calculations (Not Conversion)
Sometimes, instead of converting to a whole number, you may utilize the fractional part in computations. This is common in scenarios where the fractional component holds significant meaning.
Example: You are baking a recipe that calls for 2 ½ cups of flour. Instead of rounding up or down, you'll measure out 2 ½ cups precisely.
Addressing Common Misconceptions
-
You can't directly convert: It's crucial to understand that a direct conversion from a mixed fraction to a whole number without losing information isn't mathematically possible. You can only approximate or find a related whole number representation, based on the context.
-
Rounding isn't always sufficient: Simple rounding might not be accurate enough for specific applications demanding greater precision.
-
Context is key: The best method depends on the practical implications and the level of accuracy required.
Choosing the Right Method: A Summary
The choice of method hinges on your specific needs:
-
For estimations and quick calculations: Rounding to the nearest whole number (Method 1) is sufficient.
-
For practical scenarios where rounding up or down is necessary based on the context: Method 2 is appropriate.
-
For a more accurate approximation based on the size of the fractional part: Method 3 is useful.
-
When the denominator plays a significant role: Method 4 provides a helpful approach.
-
When the fractional part is integral to the calculation: Method 5 is the appropriate method to choose.
By understanding these different approaches, you can confidently handle mixed fractions and choose the most effective method to deal with them in your specific situation. Remember, the goal is not always to eliminate the fraction but to use the best strategy that works best given the context of your problem.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 45 And 30
Apr 04, 2025
-
How Many Weeks In Four Months
Apr 04, 2025
-
28 Celsius Is What In Fahrenheit
Apr 04, 2025
-
9 To The Power Of 10
Apr 04, 2025
-
What Is The Lcm For 16 And 24
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How To Convert A Mixed Fraction To A Whole Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
