How To Find Lateral Area Of Cone
News Co
Apr 03, 2025 · 5 min read
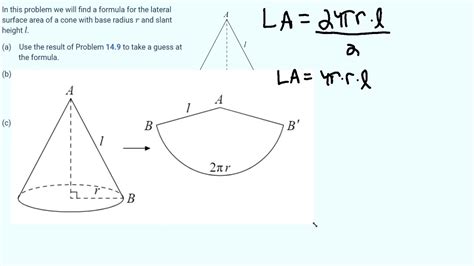
Table of Contents
How to Find the Lateral Surface Area of a Cone: A Comprehensive Guide
Finding the lateral surface area of a cone might seem daunting at first, but with a clear understanding of the formula and a few practice problems, it becomes straightforward. This comprehensive guide will walk you through the process, covering various aspects, from understanding the basic concepts to tackling more complex scenarios. We'll also explore the relationship between the lateral surface area and other cone properties, and delve into real-world applications.
Understanding the Cone and its Components
Before diving into the calculations, let's establish a solid foundation by defining key terms related to a cone:
-
Cone: A three-dimensional geometric shape that tapers smoothly from a flat base (usually circular) to a point called the apex or vertex.
-
Radius (r): The distance from the center of the circular base to any point on the circumference.
-
Height (h): The perpendicular distance from the apex to the center of the circular base.
-
Slant Height (l): The distance from the apex to any point on the circumference of the base. This is crucial for calculating the lateral surface area.
-
Lateral Surface Area: The curved surface area of the cone, excluding the base. This is what we'll be focusing on.
-
Total Surface Area: The sum of the lateral surface area and the area of the circular base.
The Formula for Lateral Surface Area of a Cone
The formula for the lateral surface area (LSA) of a cone is:
LSA = πrl
Where:
- π (pi): A mathematical constant, approximately equal to 3.14159.
- r: The radius of the circular base.
- l: The slant height of the cone.
This formula is derived from the concept of unrolling the cone's lateral surface into a sector of a circle. The arc length of this sector is equal to the circumference of the cone's base (2πr), and the radius of this sector is the slant height (l). The area of this sector is then (1/2) * arc length * radius = (1/2) * 2πr * l = πrl.
Calculating the Slant Height (l)
Often, you won't be directly given the slant height (l). Instead, you'll have the radius (r) and height (h). In such cases, you need to use the Pythagorean theorem to find the slant height. The slant height, radius, and height form a right-angled triangle, where the slant height is the hypotenuse:
l² = r² + h²
Therefore, the slant height can be calculated as:
l = √(r² + h²)
This step is crucial and often the source of errors in calculations. Remember to correctly apply the Pythagorean theorem before substituting into the lateral surface area formula.
Step-by-Step Calculation of Lateral Surface Area
Let's illustrate the calculation with a step-by-step example:
Problem: Find the lateral surface area of a cone with a radius of 5 cm and a height of 12 cm.
Step 1: Calculate the slant height (l).
Using the Pythagorean theorem:
l = √(r² + h²) = √(5² + 12²) = √(25 + 144) = √169 = 13 cm
Step 2: Apply the lateral surface area formula.
LSA = πrl = π * 5 cm * 13 cm = 65π cm²
Step 3: Calculate the numerical value.
Using π ≈ 3.14159:
LSA ≈ 65 * 3.14159 cm² ≈ 204.20335 cm²
Therefore, the lateral surface area of the cone is approximately 204.20 square centimeters.
Dealing with Different Units
Remember that consistency in units is vital. If the radius is given in meters and the height in centimeters, convert both to the same unit (either meters or centimeters) before applying the formulas. Failing to do so will lead to incorrect results. Always state your final answer with appropriate units.
Practical Applications and Real-World Examples
The concept of lateral surface area has numerous practical applications across various fields:
-
Engineering: Calculating the surface area of conical structures like silos, funnels, and water towers is crucial for material estimation and cost calculations.
-
Architecture: Designing conical roofs or other architectural elements requires precise calculations of surface area for material selection and construction planning.
-
Manufacturing: Manufacturing conical containers, such as ice cream cones or party hats, requires accurate lateral surface area calculations to determine the amount of material needed.
-
Packaging: Designing packaging with conical shapes involves calculating the lateral surface area to ensure the package can hold the intended product.
Advanced Concepts and Variations
While the basic formula serves most purposes, certain situations may require more nuanced approaches:
-
Frustums: A frustum is the portion of a cone remaining after its top is cut off by a plane parallel to its base. Calculating its lateral surface area requires a modified formula involving the radii of both bases and the slant height of the frustum.
-
Oblique Cones: Unlike right cones (where the apex is directly above the center of the base), oblique cones have their apex off-center. Calculating their lateral surface area requires more advanced methods, often involving integral calculus.
-
Cones with non-circular bases: Although less common, cones can have elliptical or other shaped bases. The calculation of the lateral surface area becomes significantly more complex in these cases.
Troubleshooting Common Mistakes
Many errors arise from:
-
Incorrectly identifying r, h, and l: Double-check that you've correctly identified the radius, height, and slant height before applying the formulas.
-
Mistakes in Pythagorean theorem: Carefully calculate the slant height using the Pythagorean theorem. A small error here will propagate through the rest of the calculation.
-
Unit inconsistency: Ensure consistent units throughout the calculation.
-
Rounding errors: Avoid premature rounding. Keep intermediate values to a sufficient number of decimal places before rounding your final answer.
Further Exploration and Practice Problems
To solidify your understanding, try solving various practice problems with different values for radius and height. Explore online resources and textbooks for additional problems and challenges involving frustums and oblique cones. The more you practice, the more comfortable and confident you will become in calculating the lateral surface area of cones.
This comprehensive guide provides a thorough understanding of how to find the lateral surface area of a cone, covering the fundamental concepts, step-by-step calculations, practical applications, and potential pitfalls. Remember that consistent practice and attention to detail are key to mastering this important geometric concept.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 45 And 30
Apr 04, 2025
-
How Many Weeks In Four Months
Apr 04, 2025
-
28 Celsius Is What In Fahrenheit
Apr 04, 2025
-
9 To The Power Of 10
Apr 04, 2025
-
What Is The Lcm For 16 And 24
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How To Find Lateral Area Of Cone . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
