How To Find The Perpendicular Line Of A Slope
News Co
Mar 30, 2025 · 6 min read
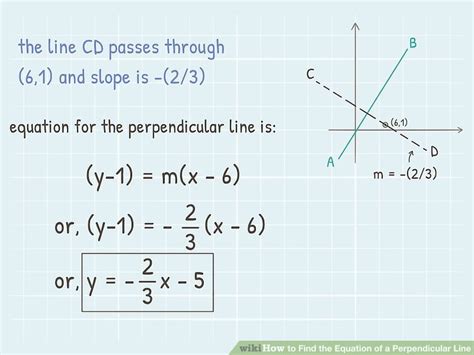
Table of Contents
How to Find the Perpendicular Line of a Slope
Finding the perpendicular line of a given slope is a fundamental concept in geometry and has wide-ranging applications in various fields, including engineering, physics, and computer graphics. Understanding this concept is crucial for solving problems related to angles, distances, and intersections of lines. This comprehensive guide will break down the process step-by-step, providing clear explanations and practical examples to solidify your understanding.
Understanding Slopes and Perpendicular Lines
Before diving into the calculations, let's refresh our understanding of slopes and their relationship to perpendicular lines.
What is a Slope?
The slope of a line, often represented by the letter m, describes its steepness or inclination. It's calculated as the ratio of the vertical change (rise) to the horizontal change (run) between any two distinct points on the line. Formally:
m = (y2 - y1) / (x2 - x1)
Where (x1, y1) and (x2, y2) are two points on the line. A positive slope indicates an upward incline from left to right, a negative slope indicates a downward incline, a slope of zero represents a horizontal line, and an undefined slope signifies a vertical line.
The Relationship Between Perpendicular Lines and their Slopes
Two lines are perpendicular if they intersect at a right angle (90°). The relationship between the slopes of perpendicular lines is key to finding the equation of a perpendicular line. The slopes of two perpendicular lines are negative reciprocals of each other. This means:
- If the slope of one line is m, the slope of the perpendicular line is -1/m.
- If one line has a slope of 0 (horizontal), its perpendicular line will have an undefined slope (vertical).
- If one line has an undefined slope (vertical), its perpendicular line will have a slope of 0 (horizontal).
This fundamental relationship forms the basis for our calculations.
Methods for Finding the Perpendicular Line
There are several methods to find the equation of a line perpendicular to a given line. The approach depends on the information available: whether you have the slope of the original line, the equation of the original line, or two points on the original line.
Method 1: Given the Slope of the Original Line
This is the simplest scenario. If you know the slope of the original line, you can immediately determine the slope of the perpendicular line and then use the point-slope form of a line to find its equation.
Steps:
-
Find the negative reciprocal of the given slope: If the slope of the original line is m, the slope of the perpendicular line (m_perp) is -1/m.
-
Use the point-slope form: The point-slope form of a line is:
y - y1 = m_perp(x - x1), where (x1, y1) is a point on the perpendicular line. You'll need at least one point that lies on the perpendicular line. This point could be a point on the original line if the perpendicular line is to pass through a specific point on the original line, or it could be a separate point entirely. -
Simplify the equation: Rearrange the equation into slope-intercept form (
y = mx + b) or standard form (Ax + By = C) as needed.
Example:
Find the equation of the line perpendicular to a line with a slope of 2 that passes through the point (3, 4).
-
Negative reciprocal: The slope of the perpendicular line is -1/2.
-
Point-slope form:
y - 4 = -1/2(x - 3) -
Simplify:
y - 4 = -1/2x + 3/2 => y = -1/2x + 11/2
Therefore, the equation of the perpendicular line is y = -1/2x + 11/2.
Method 2: Given the Equation of the Original Line
If you have the equation of the original line, you can extract its slope and proceed as in Method 1.
Steps:
-
Determine the slope of the original line: Rewrite the equation in slope-intercept form (
y = mx + b). The coefficient of x is the slope (m). -
Find the negative reciprocal: Calculate the negative reciprocal of the slope to find the slope of the perpendicular line (m_perp = -1/m).
-
Use the point-slope form (or other relevant method): You will need a point. If a point is specified on the perpendicular line, use that point. If not specified, any point on the perpendicular line will do - usually the easiest point to use is the point of intersection of the original and perpendicular line. However, to find this intersection point, you will need additional information or a second equation. This can be solved using system of equations.
Example:
Find the equation of the line perpendicular to the line y = 3x + 5 and passing through the point (1,2).
-
Slope of original line: The slope is 3.
-
Negative reciprocal: The slope of the perpendicular line is -1/3.
-
Point-slope form:
y - 2 = -1/3(x - 1) -
Simplify:
y - 2 = -1/3x + 1/3 => y = -1/3x + 7/3
Therefore, the equation of the perpendicular line is y = -1/3x + 7/3.
Method 3: Given Two Points on the Original Line
If you have two points on the original line, you can first calculate its slope and then use Method 1.
Steps:
-
Calculate the slope of the original line: Use the formula
m = (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the two points. -
Find the negative reciprocal: Calculate the negative reciprocal of the slope to find m_perp.
-
Use the point-slope form: Choose either of the two original points or any other point on the perpendicular line, and substitute into the point-slope form. Simplify the equation to the desired form.
Example:
Find the equation of the line perpendicular to the line passing through points (1, 2) and (3, 6), and passing through the point (4, 1).
-
Slope of original line:
m = (6 - 2) / (3 - 1) = 4 / 2 = 2 -
Negative reciprocal: The slope of the perpendicular line is -1/2.
-
Point-slope form (using point (4,1) ):
y - 1 = -1/2(x - 4) -
Simplify:
y - 1 = -1/2x + 2 => y = -1/2x + 3
Therefore, the equation of the perpendicular line is y = -1/2x + 3.
Special Cases: Horizontal and Vertical Lines
Remember the special cases involving horizontal and vertical lines:
-
Horizontal line: A horizontal line has a slope of 0. Its perpendicular line is a vertical line with an undefined slope, and its equation is of the form
x = c, where c is a constant. -
Vertical line: A vertical line has an undefined slope. Its perpendicular line is a horizontal line with a slope of 0, and its equation is of the form
y = c, where c is a constant.
Applications of Perpendicular Lines
Understanding perpendicular lines is crucial in numerous applications:
-
Computer Graphics: Used extensively in creating and manipulating images, defining boundaries, and generating realistic reflections.
-
Physics: Essential in analyzing forces, velocities, and trajectories, particularly in mechanics and optics.
-
Engineering: Plays a critical role in structural design, ensuring stability and strength in buildings and other structures.
-
Cartography: Used in map projections and geographical information systems (GIS).
Conclusion
Finding the equation of a perpendicular line is a fundamental skill in mathematics with broad applications across many fields. By understanding the relationship between slopes and applying the methods outlined above, you can confidently tackle problems involving perpendicular lines, whether you are given the slope, the equation, or two points of the original line. Remember to consider the special cases of horizontal and vertical lines for a complete understanding of this essential concept. Consistent practice will solidify your understanding and enable you to apply these principles efficiently and effectively.
Latest Posts
Latest Posts
-
First Derivative Test And Second Derivative Test
Apr 01, 2025
-
How To Find Equation Of A Vertical Line
Apr 01, 2025
-
Is 37 A Prime Number Or A Composite Number
Apr 01, 2025
-
What Can 19 Be Divided By
Apr 01, 2025
-
4 Divided By 9 In Fraction
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Perpendicular Line Of A Slope . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
