Is 0 A Multiple Of 2
News Co
May 08, 2025 · 5 min read
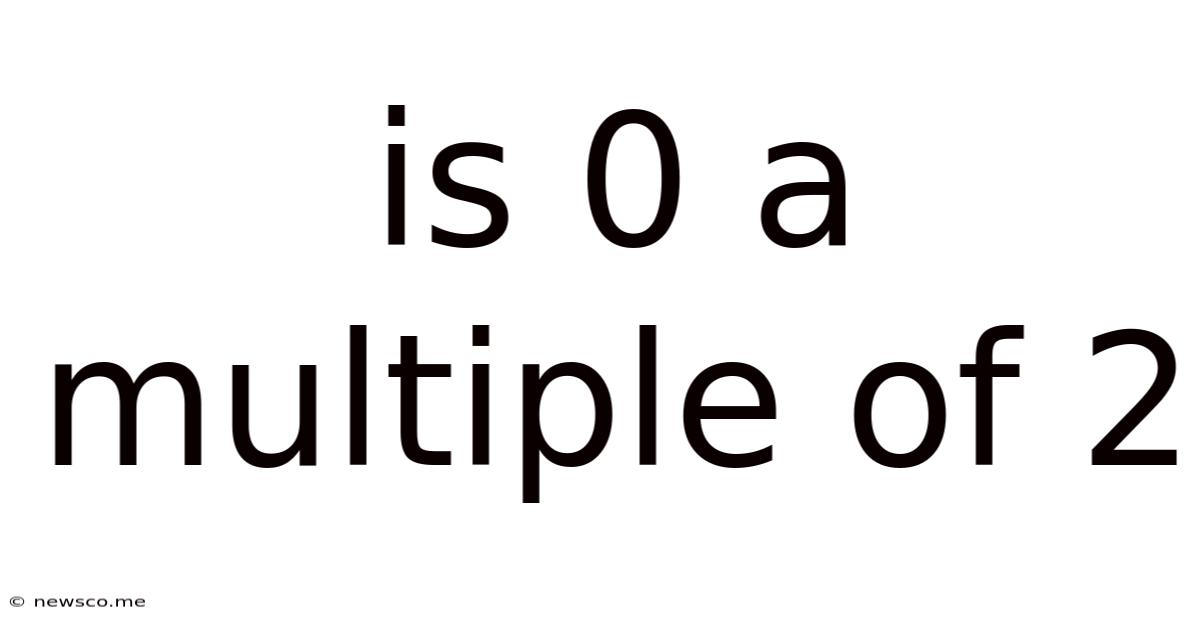
Table of Contents
Is 0 a Multiple of 2? Exploring the Concept of Multiples and Divisibility
The question, "Is 0 a multiple of 2?" might seem deceptively simple. At first glance, the answer appears obvious. However, a deeper dive into the mathematical definitions of multiples and divisibility reveals a nuanced understanding crucial for grasping fundamental arithmetic concepts. This article will explore the question comprehensively, examining the definitions, providing proofs, and addressing potential misconceptions. We'll also explore the broader implications of this seemingly simple question within mathematics and its applications.
Understanding Multiples and Divisibility
Before tackling the central question, let's establish a firm understanding of the terms "multiple" and "divisibility."
What is a Multiple?
A multiple of a number is the result of multiplying that number by an integer. For example, the multiples of 2 are 2, 4, 6, 8, 10, and so on. These are obtained by multiplying 2 by integers: 2 x 1 = 2, 2 x 2 = 4, 2 x 3 = 6, and so forth. The set of multiples of 2 extends infinitely in both positive and negative directions: ..., -8, -6, -4, -2, 0, 2, 4, 6, 8, ...
What is Divisibility?
Divisibility refers to whether a number can be divided by another number without leaving a remainder. If a number a is divisible by a number b, then there exists an integer k such that a = b x k. In other words, b is a factor of a. For instance, 12 is divisible by 3 because 12 = 3 x 4, where 4 is an integer.
Why 0 is a Multiple of 2: The Mathematical Proof
The core of the question lies in whether the definition of a multiple fits the case of zero. Let's examine this using the definition of divisibility:
A number a is a multiple of a number b if there exists an integer k such that a = b x k.
Let's set a = 0 and b = 2. We need to find an integer k that satisfies the equation 0 = 2 * k. This equation is true when k = 0, which is indeed an integer. Therefore, 0 satisfies the definition of being a multiple of 2.
In simpler terms: We can obtain 0 by multiplying 2 by 0 (an integer). Since we can express 0 as a product of 2 and an integer, 0 is a multiple of 2.
Addressing Potential Misconceptions
Some might argue that 0 is not a multiple because it's "nothing" or "not a real number" in the context of multiples. However, 0 is a perfectly valid integer, and the definition of a multiple explicitly includes the product of an integer and the given number. This misconception arises from an intuitive, rather than a formal, mathematical understanding of multiples.
Another misconception stems from thinking about multiples only in the positive realm. We often visualize multiples as a sequence of increasing numbers. However, the set of multiples of any number includes negative numbers as well. It is crucial to expand our understanding to encompass the entire number line.
0 as a Multiple of Any Integer
The principle demonstrated with 2 extends to all other integers. 0 is a multiple of every integer. This is because for any integer b, we can always find an integer k (specifically, k = 0) that satisfies the equation 0 = b x k. This confirms the universality of 0 as a multiple of any integer.
The Significance of Zero in Mathematics
Zero's role in mathematics is profound. It's not just a placeholder; it's a crucial element in various mathematical systems, including:
-
Number Systems: Zero forms the foundation of our number systems, acting as the additive identity (adding zero to any number leaves it unchanged).
-
Arithmetic Operations: Zero plays unique roles in addition, subtraction, multiplication, and division (with careful consideration for division by zero).
-
Algebra: Zero is integral to solving equations and understanding concepts such as roots and intercepts.
-
Calculus: The concept of limits and derivatives relies heavily on the behavior of functions as they approach zero.
Practical Applications and Real-World Examples
The concept of multiples, including 0 as a multiple, has various practical applications:
-
Counting and Measurement: When we count objects, zero represents the absence of objects. This naturally aligns with the concept of zero as a multiple.
-
Programming and Computer Science: Programming languages utilize zero extensively. Arrays are often indexed from 0, and zero plays a significant role in conditional statements and loops.
-
Data Analysis and Statistics: Zero is a common data point representing the absence of a particular value or phenomenon. Understanding multiples and zero is crucial for interpreting data and performing calculations.
-
Financial Accounting: Zero signifies a balance or a lack of debt or assets. Correctly handling zero values in accounting is essential.
Conclusion: Embracing the Rigor of Mathematical Definitions
The question of whether 0 is a multiple of 2 highlights the importance of precise mathematical definitions. By strictly applying the definition of multiples and divisibility, we can rigorously demonstrate that 0 is indeed a multiple of 2 and, in fact, a multiple of every integer. This understanding isn't just an academic exercise; it's foundational to a deeper grasp of arithmetic, algebra, and various applications across different fields. Moving beyond intuitive notions and embracing the rigorous language of mathematics is key to avoiding misconceptions and ensuring a solid foundation for further mathematical exploration. The seemingly simple question "Is 0 a multiple of 2?" thus opens a gateway to a much richer understanding of the fundamental principles of mathematics and its vast applications. Remembering the formal definition helps clear up ambiguity and solidifies our mathematical reasoning. The implications extend beyond just integers, demonstrating the powerful role of zero in numerical systems.
Latest Posts
Latest Posts
-
An Equation That States Two Ratios Are Equivalent
May 08, 2025
-
How Is 2 3 Not Always Equivalent To 4 6
May 08, 2025
-
Identify Which Of The Following Statements Is Correct
May 08, 2025
-
How To Find 3 4 Of A Number
May 08, 2025
-
Which Graph Shows An Odd Function
May 08, 2025
Related Post
Thank you for visiting our website which covers about Is 0 A Multiple Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.