Is Every Real Number A Irrational Number
News Co
Apr 05, 2025 · 6 min read
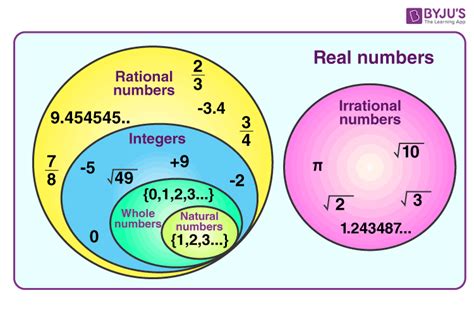
Table of Contents
Is Every Real Number an Irrational Number? A Deep Dive into Number Systems
The question, "Is every real number an irrational number?" is a deceptively simple one that delves into the fascinating world of number systems. The short answer is a resounding no. While irrational numbers are a significant part of the real number system, they don't encompass the entirety of it. This article will explore the distinctions between real numbers, rational numbers, and irrational numbers, clarifying their relationships and exploring their properties with examples. We’ll also delve into why understanding this distinction is crucial for various mathematical concepts and applications.
Understanding the Real Number System
The real number system is the foundation of much of mathematics. It's a vast and comprehensive set that encompasses all the numbers you're likely to encounter in everyday life and beyond. This system includes:
-
Rational Numbers: These are numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not zero. This includes whole numbers (like 2, -5, 0), integers (all whole numbers and their negatives), and fractions (like 1/2, -3/4, 7/1). Decimal representations of rational numbers either terminate (e.g., 0.75) or repeat (e.g., 0.333...).
-
Irrational Numbers: These numbers cannot be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating. Famous examples include π (pi), approximately 3.14159..., e (Euler's number), approximately 2.71828..., and the square root of 2 (√2), approximately 1.41421...
The real number system is the union of both rational and irrational numbers. Every point on the number line represents a real number.
The Crucial Distinction: Rational vs. Irrational
The core difference between rational and irrational numbers lies in their ability to be expressed as a ratio of two integers. This seemingly simple distinction has profound implications:
-
Rational Numbers and their Decimal Representations: As mentioned earlier, rational numbers have decimal expansions that either terminate or repeat. This is a direct consequence of their fractional form. The division process will eventually either end or fall into a recurring pattern.
-
Irrational Numbers and their Infinite, Non-repeating Decimals: Irrational numbers, in contrast, have decimal expansions that are infinite and non-repeating. This means their decimal digits go on forever without ever establishing a repeating sequence. This characteristic is a defining feature of irrationality.
Examples Illustrating the Difference
Let's consider some examples to solidify the understanding:
-
1/4 (Rational): This is a rational number because it's a fraction of integers. Its decimal representation is 0.25, which terminates.
-
2/3 (Rational): This is also rational. Its decimal representation is 0.666..., a repeating decimal.
-
√2 (Irrational): This is the length of the diagonal of a unit square. It cannot be expressed as a fraction of two integers, and its decimal expansion is non-terminating and non-repeating (approximately 1.41421356...).
-
π (Irrational): This fundamental mathematical constant, representing the ratio of a circle's circumference to its diameter, is irrational. Its decimal expansion continues infinitely without repeating.
-
e (Irrational): Euler's number, the base of the natural logarithm, is another famous irrational number with an infinite, non-repeating decimal expansion.
Why the Distinction Matters
The distinction between rational and irrational numbers is not merely a mathematical curiosity. It has significant implications across various mathematical fields:
-
Calculus: Understanding the properties of rational and irrational numbers is fundamental to calculus, particularly in dealing with limits, continuity, and integration. Many functions behave differently when evaluated at rational versus irrational points.
-
Number Theory: Number theory extensively studies the properties of integers and their relationships. The interplay between rational and irrational numbers plays a crucial role in solving many number-theoretic problems.
-
Geometry: The discovery of irrational numbers, particularly √2, revolutionized ancient Greek geometry, challenging their initial assumptions about commensurability (the ability to express ratios as fractions).
-
Real Analysis: Real analysis, a branch of mathematics concerned with the rigorous study of real numbers and functions, relies heavily on the properties of both rational and irrational numbers.
Addressing the Main Question: Not Every Real Number is Irrational
Now, we can definitively answer the initial question: No, not every real number is an irrational number. The real number system is composed of both rational and irrational numbers. The irrational numbers are a subset of the real numbers, meaning they are contained within the larger set of real numbers.
Thinking of it visually, you can imagine the real numbers as a line extending infinitely in both directions. All the points on this line represent real numbers. The rational numbers are scattered densely along this line, while the irrational numbers fill in the "gaps" between the rational numbers. In this sense, the irrational numbers are far more numerous than the rational numbers.
The fact that both rational and irrational numbers exist and make up the entirety of the real number system is a testament to the richness and complexity of mathematics.
Proofs and Demonstrations
While providing full formal mathematical proofs is beyond the scope of this article, let’s briefly touch upon the concept of demonstrating the irrationality of a number:
-
Proof by Contradiction: Many proofs of irrationality use proof by contradiction. This method assumes the number is rational, expresses it as a fraction, and then shows that this assumption leads to a logical contradiction. This contradiction proves the initial assumption (that the number is rational) must be false, hence the number is irrational. The classic proof of the irrationality of √2 uses this technique.
-
Liouville Numbers: There are specific types of numbers, such as Liouville numbers, that are proven to be transcendental (a type of irrational number which is not a root of any non-zero polynomial with rational coefficients). Their existence further demonstrates the vastness of the irrational numbers within the real number system.
Conclusion: A Broader Understanding of Numbers
Understanding the relationship between real, rational, and irrational numbers is fundamental to a deeper appreciation of mathematics. It's not simply about memorizing definitions but grasping the underlying structure and properties of these number systems. The fact that not every real number is irrational is a crucial aspect of this understanding, highlighting the distinct but interconnected nature of rational and irrational numbers within the broader context of the real number line. This knowledge provides a solid foundation for further exploration of advanced mathematical concepts. The richness of the real number system, encompassing both the seemingly orderly rational numbers and the infinitely complex irrational numbers, continues to fascinate mathematicians and contribute to the ever-evolving landscape of mathematical discovery. The journey into the world of numbers is a journey of continuous exploration and a reminder of the intricate beauty and complexity that underlies even the most fundamental mathematical concepts.
Latest Posts
Latest Posts
-
How Far Is 1 4 Of A Mile
Apr 06, 2025
-
Angles Formed By A Transversal Worksheet
Apr 06, 2025
-
Is 48 A Multiple Of 8
Apr 06, 2025
-
How Many Square Centimeters In One Square Meter
Apr 06, 2025
-
Ratios And Proportions Worksheet With Answers
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Is Every Real Number A Irrational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
