Is The Square Root Of 25 A Natural Number
News Co
May 08, 2025 · 5 min read
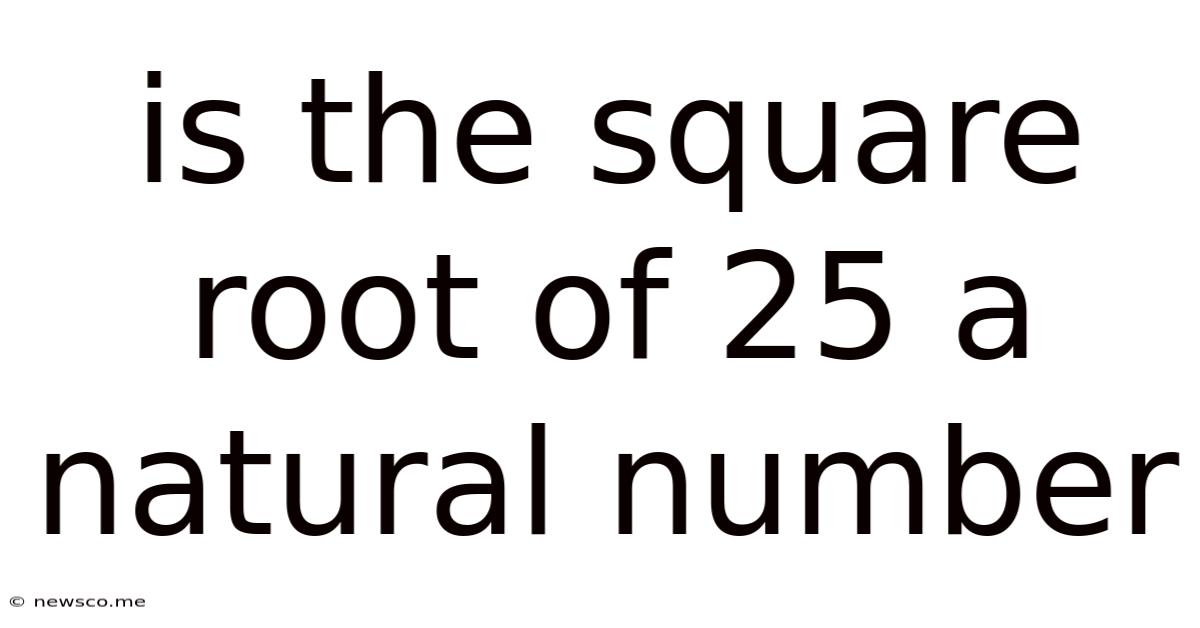
Table of Contents
Is the Square Root of 25 a Natural Number? A Deep Dive into Number Theory
The seemingly simple question, "Is the square root of 25 a natural number?" opens a fascinating window into the world of number theory. While the answer itself is straightforward, exploring the underlying concepts reveals a rich tapestry of mathematical definitions and properties. This article will delve into the intricacies of natural numbers, square roots, and the relationship between them, providing a comprehensive understanding of this fundamental mathematical concept.
Understanding Natural Numbers
Before we tackle the square root of 25, let's establish a solid foundation by defining natural numbers. These are the numbers we use for counting: 1, 2, 3, 4, and so on, extending infinitely. Zero is sometimes included in the set of natural numbers, depending on the mathematical context, but for our purposes, we'll consider the set of natural numbers as starting from 1. This set is often denoted by the symbol ℕ.
Key characteristics of natural numbers:
- Positive integers: Natural numbers are always positive whole numbers.
- Discrete: They are distinct and separate; there are no natural numbers between 2 and 3, for example.
- Countable infinity: The set of natural numbers is infinite, but it is countable, meaning we can theoretically list them out one by one, even though the process never ends.
What is a Square Root?
The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 × 3 = 9. Similarly, the square root of 16 (√16) is 4 because 4 × 4 = 16. Square roots can be represented symbolically using the radical symbol (√).
Important considerations regarding square roots:
- Positive and negative roots: Every positive number has two square roots: one positive and one negative. For example, the square roots of 25 are +5 and -5, because both 5 × 5 = 25 and (-5) × (-5) = 25.
- Principal square root: When we talk about "the" square root of a number, we usually refer to the principal square root, which is the non-negative square root. Therefore, the principal square root of 25 is 5.
- Square roots of negative numbers: The square root of a negative number is not a real number. It involves imaginary numbers, which are outside the scope of this discussion focused on natural numbers.
Solving the Problem: √25
Now, let's address the central question: Is the square root of 25 a natural number?
The square root of 25 is 5. Since 5 is a positive whole number and is part of the set of natural numbers (ℕ), the answer is a resounding yes. The principal square root of 25, which is 5, is indeed a natural number.
Expanding the Concept: Perfect Squares and Natural Numbers
Numbers like 25, which are the product of a natural number multiplied by itself (5 x 5), are called perfect squares. All perfect squares have natural numbers as their principal square roots. Here are some examples of perfect squares and their corresponding natural number square roots:
- √1 = 1
- √4 = 2
- √9 = 3
- √16 = 4
- √25 = 5
- √36 = 6
- and so on...
This relationship between perfect squares and natural numbers is a crucial aspect of number theory, illustrating the interconnectedness of various mathematical concepts.
Exploring Further: Irrational Numbers and Square Roots
Not all square roots result in natural numbers. Consider the square root of 2 (√2). This number is approximately 1.414, which is not a whole number. Numbers like √2 are called irrational numbers, meaning they cannot be expressed as a simple fraction of two integers. They have decimal representations that neither terminate nor repeat.
The contrast between the square root of 25 (a natural number) and the square root of 2 (an irrational number) highlights the diversity within the number system. Understanding this distinction is fundamental to grasping the complexities of mathematics.
The Importance of Precision in Mathematical Definitions
The seemingly simple question about the square root of 25 underscores the importance of precise definitions in mathematics. The clarity of our definitions of natural numbers and square roots allowed us to easily determine the answer. Ambiguity in definitions can lead to confusion and errors in mathematical reasoning.
Practical Applications: Real-World Examples
The concept of square roots and natural numbers isn't just confined to abstract mathematical theories; it has numerous real-world applications. For instance:
- Geometry: Calculating the side length of a square given its area involves finding the square root. If the area is 25 square units, the side length is √25 = 5 units.
- Physics: Many physics formulas involve square roots, such as calculating velocity or distance.
- Engineering: Engineers use square roots in various calculations, including structural design and circuit analysis.
- Computer Science: Square roots are essential in computer graphics, algorithms, and simulations.
Conclusion: A Simple Question with Deep Implications
The question, "Is the square root of 25 a natural number?" might seem trivial at first glance. However, exploring the answer allowed us to delve into fundamental mathematical concepts, including the definitions of natural numbers and square roots, the properties of perfect squares, and the distinction between rational and irrational numbers. This exploration demonstrates how even seemingly simple questions can lead to a deeper understanding of the rich and intricate world of mathematics and its diverse applications in various fields. Understanding these foundational concepts is crucial for anyone pursuing further studies in mathematics or related disciplines. The precision and clarity required in defining and understanding these concepts are essential for successful problem-solving and advancing our mathematical knowledge. This inquiry serves as a reminder of the elegance and power of mathematical reasoning.
Latest Posts
Latest Posts
-
2 3 Percent As A Fraction
May 08, 2025
-
Half Of 2 3 4 In Fraction
May 08, 2025
-
Which Fraction Has A Value Thats Equal To 7 8
May 08, 2025
-
Which Equation Represents The Line That Passes Through And
May 08, 2025
-
1 2 3 4 To 100
May 08, 2025
Related Post
Thank you for visiting our website which covers about Is The Square Root Of 25 A Natural Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.