Is The Square Root Of 4 A Rational Number
News Co
May 08, 2025 · 5 min read
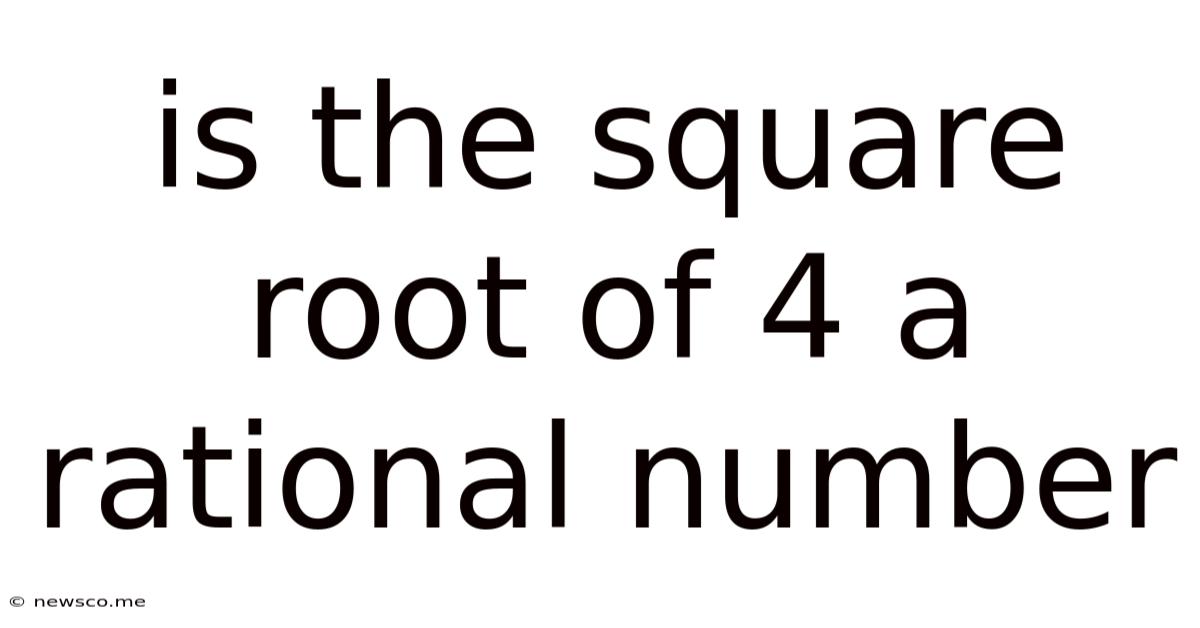
Table of Contents
Is the Square Root of 4 a Rational Number? A Deep Dive into Rationality and Irrationality
The question, "Is the square root of 4 a rational number?" might seem trivial at first glance. However, exploring this seemingly simple query opens a door to a deeper understanding of fundamental mathematical concepts like rational and irrational numbers, perfect squares, and the very nature of numbers themselves. This comprehensive article will delve into this question, providing a detailed explanation and exploring related mathematical concepts.
Understanding Rational and Irrational Numbers
Before we tackle the square root of 4, let's establish a firm understanding of the terms "rational" and "irrational." A rational number is any number that can be expressed as a fraction p/q, where p and q are integers, and q is not equal to zero. This means it can be written as a terminating or repeating decimal. Examples include 1/2 (0.5), 3/4 (0.75), and even integers like 4 (4/1).
In contrast, an irrational number cannot be expressed as a simple fraction of two integers. Their decimal representation is non-terminating and non-repeating. Famous examples include π (pi) and √2 (the square root of 2). These numbers continue infinitely without ever settling into a repeating pattern.
Calculating the Square Root of 4
The square root of a number is a value that, when multiplied by itself, equals the original number. In simpler terms, what number multiplied by itself gives you 4? The answer is clearly 2. Therefore, √4 = 2.
Is 2 a Rational Number?
Now that we know √4 = 2, the question becomes: is 2 a rational number? The answer is a resounding yes. We can express 2 as a fraction: 2/1. Here, p = 2 and q = 1, both integers, and q ≠ 0. Therefore, 2 satisfies the definition of a rational number. Its decimal representation is simply 2.0, which is a terminating decimal.
Deeper Exploration: Perfect Squares and Rational Numbers
The square root of 4 is a perfect square. A perfect square is a number that can be obtained by squaring an integer. In other words, it's the result of multiplying an integer by itself. Examples include 1 (1 x 1), 4 (2 x 2), 9 (3 x 3), 16 (4 x 4), and so on. Notice a pattern: the square root of any perfect square will always be an integer. And, as we've established, all integers are rational numbers.
Therefore, we can generalize this: the square root of any perfect square will always be a rational number. This is because the square root will always be an integer, and all integers are rational.
Contrasting with Irrational Square Roots
Let's contrast this with irrational square roots. Consider √2. This number is approximately 1.41421356..., a non-terminating, non-repeating decimal. It cannot be expressed as a fraction of two integers. Hence, √2 is an irrational number.
Similarly, √3, √5, √6, and most other square roots of non-perfect squares are irrational. Only the square roots of perfect squares are rational.
The Importance of Understanding Rationality
The distinction between rational and irrational numbers is fundamental in mathematics. It impacts various areas, including:
- Algebra: Solving equations and inequalities often involves working with rational and irrational numbers.
- Calculus: Understanding limits and continuity relies heavily on the properties of rational and irrational numbers.
- Geometry: Many geometric calculations involve irrational numbers, such as π in the calculation of a circle's circumference or area.
- Number Theory: This branch of mathematics is deeply concerned with the properties and relationships of various types of numbers, including rational and irrational numbers.
Practical Applications and Real-World Examples
While the concept might seem abstract, the distinction between rational and irrational numbers has practical applications. For instance:
- Engineering and Construction: Precise measurements often require rational numbers to ensure accuracy and avoid errors.
- Computer Science: Representing numbers in computers relies on understanding rational numbers and their limitations. Irrational numbers often need approximation for computational purposes.
- Finance: Calculations involving interest rates, investments, and loans frequently use rational numbers.
Addressing Common Misconceptions
There are some common misconceptions surrounding rational and irrational numbers. Let’s clarify them:
- All decimals are irrational: This is false. Terminating and repeating decimals are rational.
- Irrational numbers are useless: This is also false. Irrational numbers are essential in many areas of mathematics and science, as discussed above.
- Approximations make irrational numbers rational: Approximating an irrational number with a rational number doesn't change its fundamental nature. It remains irrational.
Conclusion: The Square Root of 4 is Definitely Rational
Returning to our initial question, we can definitively conclude that the square root of 4 is indeed a rational number. This stems from the fact that √4 = 2, and 2 can be expressed as the rational fraction 2/1. This seemingly simple problem serves as a gateway to understanding the broader landscape of number systems and their importance in various mathematical and scientific disciplines. The exploration of rational and irrational numbers is a journey into the heart of mathematics, revealing the elegant structures and subtle nuances that govern the world of numbers. Understanding these concepts is crucial for anyone seeking a deeper appreciation of mathematical principles and their applications in the real world. From the simple elegance of perfect squares to the infinite complexity of irrational numbers, the world of numbers continues to fascinate and challenge, reminding us of the enduring power and beauty of mathematics.
Latest Posts
Latest Posts
-
Subtract Mixed Number From Whole Number
May 08, 2025
-
How Many Glasses Of Water In 3 Liters
May 08, 2025
-
3 1 2 As A Whole Number
May 08, 2025
-
How To Find Apothem Of Octagon
May 08, 2025
-
What Is The Following Product Sqrt 12 Sqrt 18
May 08, 2025
Related Post
Thank you for visiting our website which covers about Is The Square Root Of 4 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.