Simplify 3 Square Root Of 125
News Co
May 08, 2025 · 5 min read
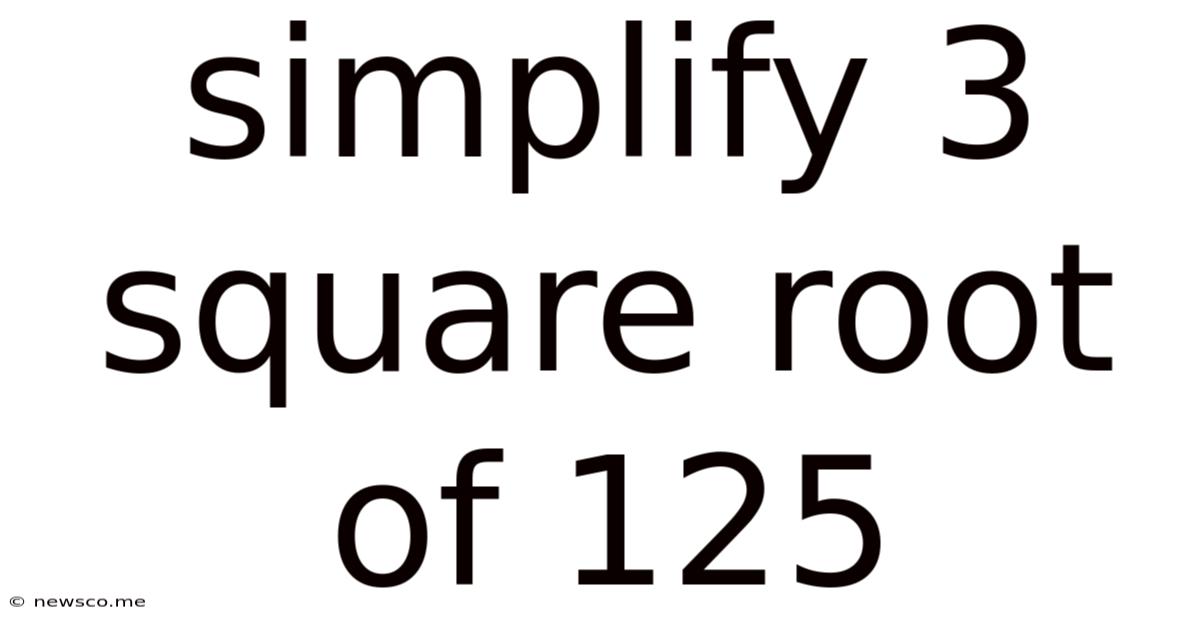
Table of Contents
Simplifying √125: A Comprehensive Guide
Simplifying radicals, such as the cube root of 125 (∛125), is a fundamental concept in algebra. Understanding how to simplify these expressions is crucial for success in higher-level mathematics. This comprehensive guide will walk you through the process of simplifying ∛125, providing a step-by-step approach and exploring the underlying mathematical principles. We'll also delve into the broader context of simplifying cube roots, providing you with the tools to tackle similar problems with confidence.
Understanding Cube Roots
Before we dive into simplifying ∛125, let's establish a clear understanding of cube roots. A cube root is a number that, when multiplied by itself three times, equals a given number. In other words, if x³ = y, then x is the cube root of y (written as ∛y). For example:
- ∛8 = 2 because 2 x 2 x 2 = 8
- ∛27 = 3 because 3 x 3 x 3 = 27
- ∛64 = 4 because 4 x 4 x 4 = 64
Unlike square roots, which can have both positive and negative solutions, cube roots have only one real solution. This simplifies the process of simplification considerably.
Prime Factorization: The Key to Simplification
The most efficient method for simplifying cube roots involves prime factorization. Prime factorization is the process of breaking down a number into its prime factors – numbers that are only divisible by 1 and themselves. For example, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3).
This technique is crucial because it allows us to identify groups of three identical factors, which can then be extracted from the cube root. This is based on the property of radicals that states: ∛(a x a x a) = a.
Step-by-Step Simplification of ∛125
Now, let's apply prime factorization to simplify ∛125:
-
Find the prime factorization of 125: We can start by dividing 125 by the smallest prime number, 2. Since 125 is not divisible by 2, we move to the next prime number, 3. 125 is not divisible by 3 either. The next prime number is 5, and 125 is divisible by 5 (125 ÷ 5 = 25). 25 is also divisible by 5 (25 ÷ 5 = 5). Therefore, the prime factorization of 125 is 5 x 5 x 5, or 5³.
-
Rewrite the cube root using the prime factorization: Now we can rewrite ∛125 as ∛(5 x 5 x 5).
-
Extract the perfect cube: Since we have three identical factors of 5, we can extract one 5 from the cube root. This is because ∛(5 x 5 x 5) = 5.
Therefore, the simplified form of ∛125 is 5.
Beyond ∛125: Simplifying Other Cube Roots
The same process applies to simplifying other cube roots. Let's consider a few more examples:
Example 1: Simplifying ∛216
-
Prime factorization of 216: 216 = 2 x 2 x 2 x 3 x 3 x 3 = 2³ x 3³
-
Rewrite the cube root: ∛216 = ∛(2³ x 3³)
-
Extract perfect cubes: ∛(2³ x 3³) = 2 x 3 = 6
Therefore, ∛216 simplifies to 6.
Example 2: Simplifying ∛1000
-
Prime factorization of 1000: 1000 = 10 x 10 x 10 = (2 x 5) x (2 x 5) x (2 x 5) = 2³ x 5³
-
Rewrite the cube root: ∛1000 = ∛(2³ x 5³)
-
Extract perfect cubes: ∛(2³ x 5³) = 2 x 5 = 10
Therefore, ∛1000 simplifies to 10.
Example 3: Simplifying ∛54
-
Prime factorization of 54: 54 = 2 x 3 x 3 x 3 = 2 x 3³
-
Rewrite the cube root: ∛54 = ∛(2 x 3³)
-
Extract perfect cubes: ∛(2 x 3³) = 3∛2
Therefore, ∛54 simplifies to 3∛2. Note that in this case, we couldn't extract a perfect cube for the factor 2, so it remains inside the cube root.
Working with Variables
The principles of prime factorization and simplifying cube roots also extend to expressions involving variables. Consider the following example:
Example 4: Simplifying ∛(8x³y⁶)
-
Prime factorization: 8x³y⁶ = 2³ x x³ x y⁶
-
Rewrite the cube root: ∛(2³ x x³ x y⁶)
-
Extract perfect cubes: We can extract one 2, one x, and two y's (because y⁶ = y³ x y³). This gives us 2xy².
Therefore, ∛(8x³y⁶) simplifies to 2xy².
Common Mistakes to Avoid
When simplifying cube roots, several common mistakes can lead to incorrect results. Here are a few to watch out for:
-
Incorrect prime factorization: Ensure you correctly break down the number into its prime factors. A single missed or incorrect factor will lead to an incorrect simplification.
-
Forgetting to extract all perfect cubes: Make sure you extract all groups of three identical factors from the cube root. Leaving any behind will result in an unsimplified expression.
-
Incorrect handling of variables: When dealing with variables, ensure you correctly apply the exponent rules for cube roots. Remember that ∛(xⁿ) = x^(n/3).
-
Confusing cube roots with square roots: Remember that the rules for simplifying cube roots are different from those for square roots. Don't apply square root rules to cube roots.
Advanced Applications and Further Exploration
Simplifying cube roots is a fundamental skill that serves as a building block for more complex algebraic manipulations. It's essential in various areas of mathematics, including:
-
Solving cubic equations: Simplifying cube roots is often necessary when finding the solutions to cubic equations.
-
Calculus: Cube roots appear frequently in calculus problems involving integration and differentiation.
-
Geometry: Cube roots are used in calculating volumes and surface areas of three-dimensional shapes.
-
Physics and engineering: Cube roots appear in numerous formulas and equations across various branches of science and engineering.
By mastering the techniques outlined in this guide, you'll not only be able to simplify cube roots efficiently but also develop a deeper understanding of fundamental algebraic concepts. Remember to practice regularly, working through various examples to solidify your understanding and build your confidence. The more you practice, the more effortlessly you'll be able to simplify these expressions. And don't hesitate to revisit the steps and examples provided here whenever needed. Consistent practice and review are key to mastering this important mathematical skill.
Latest Posts
Latest Posts
-
How Many Ounces Are Ina Liter
May 08, 2025
-
Determine If The Function Below Is Continuous
May 08, 2025
-
A Parallelogram With 4 Right Angles
May 08, 2025
-
The Polynomial X3 8 Is Equal To
May 08, 2025
-
What Is The Length Of A Line Segment
May 08, 2025
Related Post
Thank you for visiting our website which covers about Simplify 3 Square Root Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.