The Polynomial X3 + 8 Is Equal To
News Co
May 08, 2025 · 5 min read
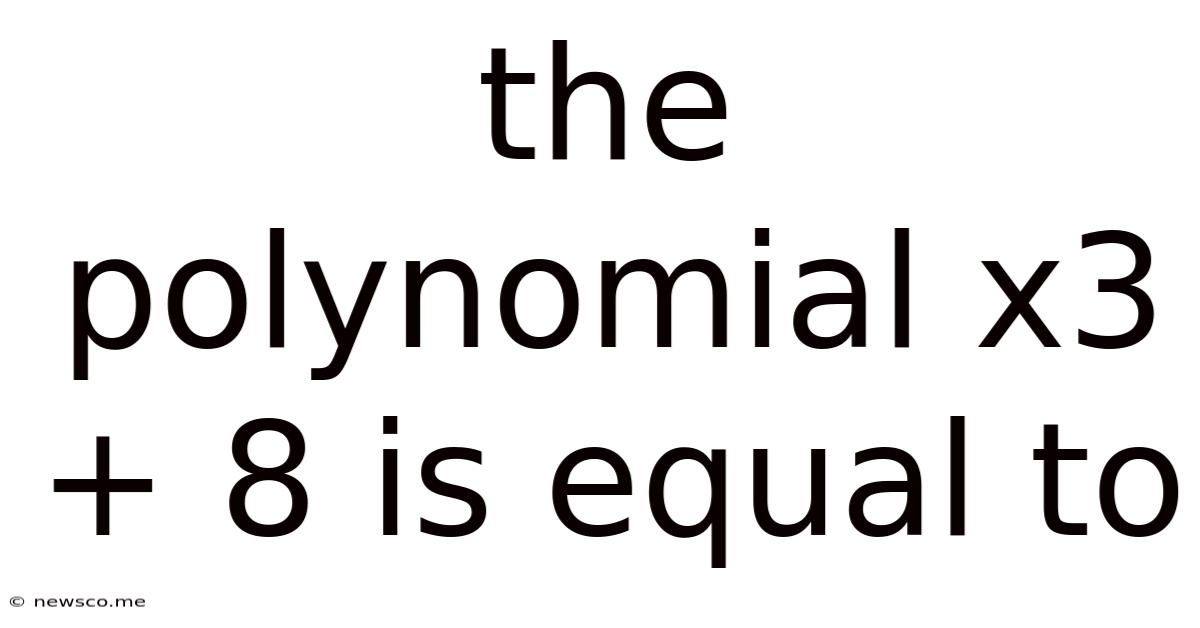
Table of Contents
The Polynomial x³ + 8: A Comprehensive Exploration
The seemingly simple polynomial expression, x³ + 8, holds a wealth of mathematical richness that extends far beyond its initial appearance. This article delves into a comprehensive analysis of this cubic polynomial, exploring its factorization, roots, graphical representation, and its applications within various mathematical contexts. We will uncover its hidden depths, revealing its connections to complex numbers, geometry, and even calculus.
Factoring x³ + 8: Unveiling the Sum of Cubes
The expression x³ + 8 can be elegantly factored using the sum of cubes formula, a fundamental concept in algebra. This formula states that:
a³ + b³ = (a + b)(a² - ab + b²)
In our case, a = x and b = 2 (since 8 = 2³). Applying the formula, we get:
x³ + 8 = (x + 2)(x² - 2x + 4)
This factorization is crucial because it breaks down a complex cubic expression into simpler, manageable components. The first factor, (x + 2), is a linear term, while the second factor, (x² - 2x + 4), is a quadratic term. This decomposition allows for easier analysis of the polynomial's roots and behavior.
Finding the Roots: Delving into the Solutions
The roots of a polynomial are the values of x that make the polynomial equal to zero. Finding the roots of x³ + 8 is equivalent to solving the equation x³ + 8 = 0. Using the factorization above, we can find the roots by setting each factor to zero:
-
x + 2 = 0 => x = -2 This is a real root.
-
x² - 2x + 4 = 0 This quadratic equation requires further analysis. We can use the quadratic formula to find its roots:
x = [-b ± √(b² - 4ac)] / 2a
where a = 1, b = -2, and c = 4. Substituting these values:
x = [2 ± √((-2)² - 4 * 1 * 4)] / 2 * 1 = [2 ± √(-12)] / 2 = [2 ± 2i√3] / 2 = 1 ± i√3
Therefore, the roots of x² - 2x + 4 are x = 1 + i√3 and x = 1 - i√3. These are complex conjugate roots.
In summary, the polynomial x³ + 8 has three roots: one real root (-2) and two complex conjugate roots (1 + i√3 and 1 - i√3). This demonstrates a fundamental property of polynomial equations: a polynomial of degree n will have exactly n roots (counting multiplicity), some of which may be real and some complex.
Graphical Representation: Visualizing the Polynomial
The graphical representation of x³ + 8 provides a visual understanding of its behavior. The graph of the function y = x³ + 8 is a cubic curve that intersects the x-axis at its roots. The real root, x = -2, is clearly visible as the point where the curve crosses the x-axis. The complex roots, however, do not appear on the real x-y plane.
The graph displays the following key features:
-
Increasing Function: The function is monotonically increasing, meaning it consistently rises as x increases. This is a characteristic of odd-degree polynomials.
-
y-intercept: The y-intercept occurs when x = 0, resulting in y = 8. This is easily seen on the graph.
-
Asymptotic Behavior: As x approaches positive or negative infinity, the value of y also approaches positive or negative infinity respectively.
Applications and Extensions: Beyond the Basics
The seemingly simple polynomial x³ + 8 finds applications in various areas of mathematics and beyond:
-
Calculus: The derivative and integral of x³ + 8 are straightforward to calculate, offering insights into the function's rate of change and accumulation. The derivative, 3x², represents the slope of the tangent line at any point on the curve. The integral, (1/4)x⁴ + 8x + C, represents the area under the curve.
-
Geometry: The polynomial can be used in geometrical problems, particularly those involving volumes of solids. For example, the volume of a certain type of solid might be expressed by such a polynomial equation.
-
Complex Analysis: The complex roots of the polynomial demonstrate the importance of complex numbers in understanding polynomial equations. Complex analysis extensively utilizes such concepts to analyze and solve complex mathematical problems.
-
Engineering and Physics: Cubic equations, similar to x³ + 8, often appear in the modelling of physical phenomena, particularly in scenarios involving three-dimensional spatial relationships or dynamic systems.
Exploring Related Concepts: Expanding the Knowledge Base
Understanding x³ + 8 opens doors to related mathematical concepts:
-
Difference of Cubes: In contrast to the sum of cubes, the difference of cubes formula (a³ - b³ = (a - b)(a² + ab + b²)) provides a parallel factorization technique for expressions of the form x³ - 8.
-
Higher-Degree Polynomials: The methods used to analyze x³ + 8 can be extended to higher-degree polynomials, though the complexity of finding roots increases significantly. Numerical methods are often employed for higher-degree polynomials.
-
Partial Fraction Decomposition: In calculus, the factorization of x³ + 8 plays a role in techniques like partial fraction decomposition, used to simplify the integration of rational functions.
-
Polynomial Long Division: While not strictly necessary for this specific example, polynomial long division is a powerful tool for dividing polynomials, which can be helpful when dealing with more complex polynomial expressions.
Conclusion: A Deep Dive into a Simple Polynomial
The seemingly simple polynomial x³ + 8 reveals a surprising depth of mathematical richness. Through its factorization, root analysis, graphical representation, and diverse applications, we have explored its significance across various mathematical domains. This analysis highlights the power of seemingly simple mathematical concepts and their far-reaching implications. Further exploration into these related concepts will only enrich one's mathematical understanding and problem-solving capabilities. The journey of understanding x³ + 8 serves as a microcosm of the beauty and complexity inherent in the world of mathematics. It encourages us to look beyond the surface and appreciate the intricate details that lie beneath.
Latest Posts
Latest Posts
-
Complete The Square X2 6x 13
May 09, 2025
-
Find The Length S Of The Circular Arc
May 09, 2025
-
What Is The Standard Metric Unit For Volume
May 09, 2025
-
What Is The Gcf Of 7 And 7
May 09, 2025
-
65 321 To The Nearest Ten Thousand
May 09, 2025
Related Post
Thank you for visiting our website which covers about The Polynomial X3 + 8 Is Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.