Use The Gcf To Factor 24+6x
News Co
May 08, 2025 · 5 min read
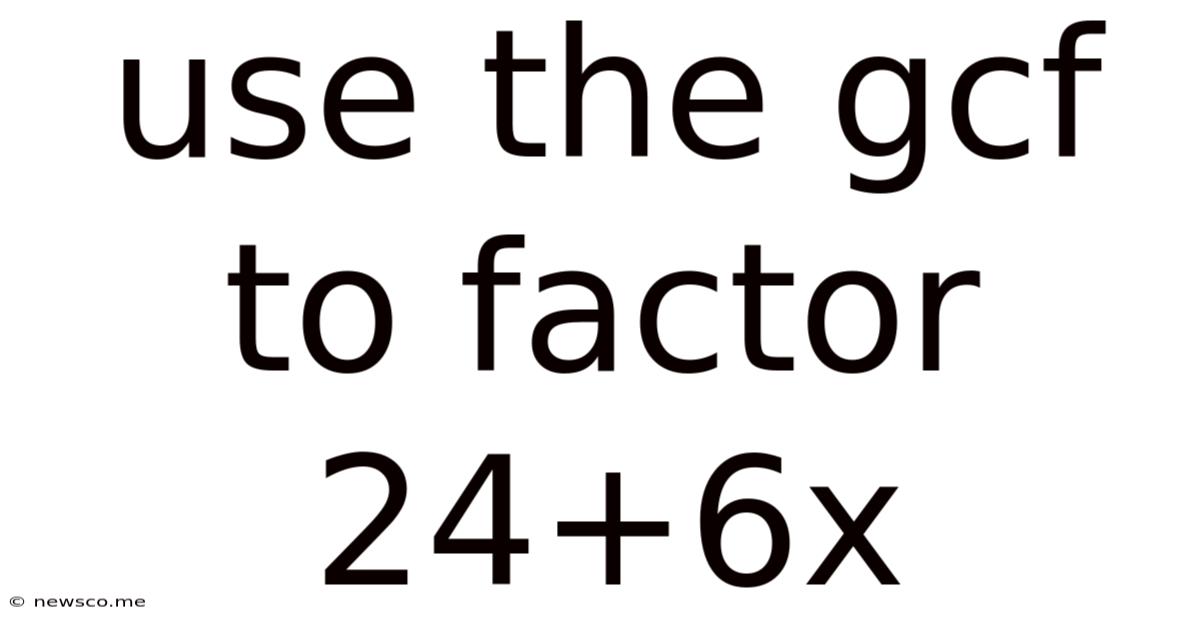
Table of Contents
Using the GCF to Factor 24 + 6x: A Comprehensive Guide
Factoring algebraic expressions is a fundamental skill in algebra. Understanding how to factor expressions efficiently and accurately is crucial for solving equations, simplifying expressions, and tackling more advanced algebraic concepts. One of the simplest yet most important factoring techniques involves using the Greatest Common Factor (GCF). This article will explore the process of factoring the expression 24 + 6x using the GCF, explaining the underlying principles and extending the concept to more complex scenarios. We'll delve deep into the method, exploring various examples and highlighting potential pitfalls to avoid.
Understanding the Greatest Common Factor (GCF)
Before we tackle the factorization of 24 + 6x, let's solidify our understanding of the GCF. The GCF of two or more numbers is the largest number that divides evenly into all of them. Similarly, when dealing with algebraic terms containing variables, the GCF incorporates both numerical and variable components.
Finding the GCF:
To find the GCF, we typically break down each number into its prime factorization. The prime factorization is the expression of a number as a product of its prime factors (numbers divisible only by 1 and themselves). Let's illustrate this with an example:
Find the GCF of 24 and 6:
- Prime factorization of 24: 2 x 2 x 2 x 3 = 2³ x 3
- Prime factorization of 6: 2 x 3
Comparing the prime factorizations, we see that both 24 and 6 share one factor of 2 and one factor of 3. Therefore, the GCF of 24 and 6 is 2 x 3 = 6.
Factoring 24 + 6x Using the GCF
Now, let's apply this concept to the expression 24 + 6x. Both 24 and 6x are terms in the expression. We need to identify the GCF of 24 and 6x.
-
Find the GCF of the numerical coefficients: As shown above, the GCF of 24 and 6 is 6.
-
Identify common variables: Both terms contain the variable 'x', but only 6x has an 'x'. This means 'x' is not a common factor for both terms.
-
Determine the GCF of the entire expression: Combining the numerical GCF, the GCF of 24 and 6x is 6.
-
Factor out the GCF: We now factor out the GCF (6) from both terms:
24 + 6x = 6(4 + x)
Verification:
To verify our factorization, we can expand the factored expression:
6(4 + x) = 6 * 4 + 6 * x = 24 + 6x
This confirms that our factorization is correct.
Expanding the Concept: More Complex Examples
The GCF method is not limited to simple expressions like 24 + 6x. Let's consider more complex scenarios:
Example 1: Factoring 15x² + 25x
-
Numerical GCF: The GCF of 15 and 25 is 5.
-
Variable GCF: Both terms contain 'x', and the lowest power of 'x' is x¹. Therefore, the variable GCF is x.
-
Overall GCF: The GCF of 15x² and 25x is 5x.
-
Factoring: 15x² + 25x = 5x(3x + 5)
Example 2: Factoring 12a³b² - 18a²b + 6ab
-
Numerical GCF: The GCF of 12, 18, and 6 is 6.
-
Variable GCF: All terms contain 'a' and 'b'. The lowest power of 'a' is a¹, and the lowest power of 'b' is b¹. Therefore, the variable GCF is ab.
-
Overall GCF: The GCF of 12a³b², -18a²b, and 6ab is 6ab.
-
Factoring: 12a³b² - 18a²b + 6ab = 6ab(2a²b - 3a + 1)
Common Mistakes to Avoid
While the GCF method is relatively straightforward, several common mistakes can hinder the factoring process:
-
Not finding the greatest common factor: Failing to identify the largest possible common factor will result in an incomplete factorization. Always ensure you've found the largest numerical and variable GCF.
-
Incorrect sign distribution: When factoring out a negative GCF, ensure you correctly distribute the negative sign to all terms within the parentheses. For example, factoring -12x - 6 should yield -6(2x + 1), not -6(2x - 1).
-
Forgetting to check your work: Always expand your factored expression to verify that it is equivalent to the original expression. This simple step helps catch errors and build confidence.
Applications of GCF Factoring
GCF factoring is a cornerstone of many algebraic manipulations and problem-solving techniques. Its applications extend to:
-
Solving quadratic equations: Factoring is often the first step in solving quadratic equations by setting each factor to zero.
-
Simplifying rational expressions: GCF factoring simplifies rational expressions (fractions with algebraic terms) by canceling common factors in the numerator and denominator.
-
Finding roots and zeros: The factors of an expression directly correspond to the roots (or zeros) of the associated equation.
-
Graphing polynomial functions: The factored form of a polynomial can provide valuable information about the x-intercepts and behavior of the graph.
Beyond the Basics: Further Exploration
While we've focused on factoring using the GCF, it's important to note that this is just one of several factoring techniques. Other important methods include:
-
Difference of squares: Factoring expressions in the form a² - b² = (a + b)(a - b).
-
Trinomial factoring: Factoring quadratic trinomials of the form ax² + bx + c.
-
Grouping: A technique used to factor expressions with four or more terms.
Mastering GCF factoring is essential for building a strong foundation in algebra. It's a versatile tool used across many algebraic concepts and is a crucial stepping stone to more advanced factoring techniques. By understanding the underlying principles and practicing regularly, you'll develop the skills to factor a wide range of algebraic expressions confidently and efficiently. Remember to always check your work and explore the various applications of this fundamental algebraic skill.
Latest Posts
Latest Posts
-
Can Sample Variance Be Equal To Population Variance
May 09, 2025
-
Events That Cannot Occur At The Same Time Are Called
May 09, 2025
-
What Is 10 4 As A Decimal
May 09, 2025
-
What Does Area Under The Curve Mean In Statistics
May 09, 2025
-
8 1 4 As A Fraction
May 09, 2025
Related Post
Thank you for visiting our website which covers about Use The Gcf To Factor 24+6x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.