What Are The Factors For 66
News Co
Apr 08, 2025 · 5 min read
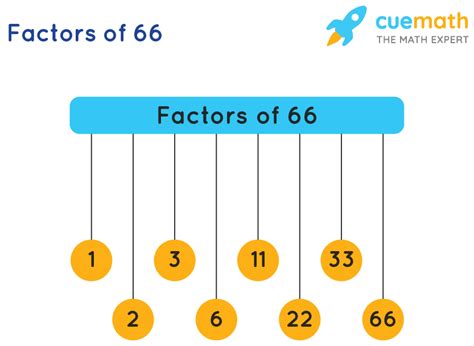
Table of Contents
Decoding the Enigma: Exploring the Factors of 66
The number 66, seemingly innocuous at first glance, holds a fascinating depth when explored through the lens of mathematics. Understanding its factors unveils a deeper appreciation for fundamental number theory and its applications. This article delves into the comprehensive analysis of the factors of 66, exploring various methods of identification, their mathematical properties, and the broader implications within the field of number theory.
What are Factors?
Before diving into the specifics of 66, let's establish a clear definition. In mathematics, a factor (or divisor) of a number is an integer that divides the number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 evenly. Finding all the factors of a number is a fundamental concept in arithmetic and algebra, forming the basis for more advanced mathematical concepts.
Finding the Factors of 66: A Step-by-Step Approach
There are several methods to determine the factors of 66. Let's explore two common approaches:
1. The Brute-Force Method
This method involves systematically checking each integer from 1 up to 66 to see if it divides 66 without a remainder. While straightforward, it can be time-consuming for larger numbers.
- 1: 66 ÷ 1 = 66 (1 is a factor)
- 2: 66 ÷ 2 = 33 (2 is a factor)
- 3: 66 ÷ 3 = 22 (3 is a factor)
- 4: 66 ÷ 4 = 16.5 (4 is not a factor)
- 5: 66 ÷ 5 = 13.2 (5 is not a factor)
- 6: 66 ÷ 6 = 11 (6 is a factor)
- 7: 66 ÷ 7 ≈ 9.43 (7 is not a factor)
- 8: 66 ÷ 8 = 8.25 (8 is not a factor)
- 9: 66 ÷ 9 ≈ 7.33 (9 is not a factor)
- 10: 66 ÷ 10 = 6.6 (10 is not a factor)
- 11: 66 ÷ 11 = 6 (11 is a factor)
We continue this process until we reach the square root of 66 (approximately 8.12). After this point, the remaining factors will be the pairs we've already identified, just reversed. Therefore, the factors of 66 are 1, 2, 3, 6, 11, 22, 33, and 66.
2. Prime Factorization Method
This is a more efficient method, especially for larger numbers. It involves expressing the number as a product of its prime factors. Prime factors are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
The prime factorization of 66 is 2 x 3 x 11. Once we have the prime factorization, we can systematically find all the factors by combining these primes in different ways:
- 1: (no primes)
- 2: 2
- 3: 3
- 6: 2 x 3
- 11: 11
- 22: 2 x 11
- 33: 3 x 11
- 66: 2 x 3 x 11
This method confirms our findings from the brute-force approach: the factors of 66 are 1, 2, 3, 6, 11, 22, 33, and 66.
Properties of the Factors of 66
The factors of 66 exhibit several interesting properties:
- Even and Odd Factors: The factors include both even (2, 6, 22, 66) and odd (1, 3, 11, 33) numbers.
- Sum of Factors: The sum of the factors (1 + 2 + 3 + 6 + 11 + 22 + 33 + 66) equals 144. This sum is significant in number theory, particularly in the context of abundant, deficient, and perfect numbers. 66 is an abundant number because the sum of its proper divisors (excluding itself) is greater than 66.
- Divisibility Rules: The factors of 66 demonstrate the divisibility rules for 2, 3, and 11. A number is divisible by 2 if it's even, by 3 if the sum of its digits is divisible by 3, and by 11 if the alternating sum of its digits is divisible by 11.
Applications and Significance in Number Theory
Understanding factors is crucial in various areas of mathematics and beyond:
- Greatest Common Divisor (GCD): Finding the GCD of two or more numbers, the largest number that divides all of them without a remainder, relies on factor analysis. This has applications in simplifying fractions, solving Diophantine equations, and cryptography.
- Least Common Multiple (LCM): The LCM is the smallest number divisible by two or more numbers. It is crucial in solving problems involving fractions, cycles, and scheduling.
- Modular Arithmetic: Factors play a vital role in modular arithmetic, the system of arithmetic for integers where numbers "wrap around" upon reaching a certain value (the modulus). This is extensively used in cryptography and computer science.
- Number Theory Research: The study of factors and divisors contributes to broader research in number theory, including the Riemann Hypothesis and Goldbach's conjecture.
Expanding the Understanding: Beyond Basic Factorization
While finding the factors of 66 provides a solid foundation, delving deeper into number theory opens up a world of complexities and fascinating connections. Concepts like:
- Tau Function (τ(n)): This function counts the number of divisors of an integer n. For 66, τ(66) = 8, representing the eight factors we identified.
- Sigma Function (σ(n)): This function calculates the sum of all divisors of an integer n. For 66, σ(66) = 144, as previously calculated.
- Perfect Numbers, Abundant Numbers, and Deficient Numbers: These classifications of numbers are defined by the relationship between a number and the sum of its proper divisors. 66, as mentioned earlier, is an abundant number.
These advanced concepts demonstrate the significance of factor analysis as a stepping stone towards more complex mathematical explorations.
Conclusion: The Enduring Significance of Factors
The seemingly simple task of finding the factors of 66 unveils a rich tapestry of mathematical concepts and applications. From the basic methods of identification to the more advanced concepts in number theory, understanding factors forms a critical foundation in various branches of mathematics and its applications in computer science, cryptography, and beyond. The seemingly humble number 66, therefore, serves as a potent example of the inherent beauty and complexity found within the seemingly simple realm of arithmetic. Further exploration of these concepts will undoubtedly lead to a deeper appreciation for the elegance and power of mathematical reasoning.
Latest Posts
Latest Posts
-
Examples Of Polynomials And Non Polynomials
Apr 08, 2025
-
How Many Water Bottles Equal A Gallon Of Water
Apr 08, 2025
-
Is 101 A Prime Or Composite Number
Apr 08, 2025
-
Lcm Of 6 8 And 4
Apr 08, 2025
-
How Much Is 26 Celsius In Fahrenheit
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factors For 66 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.