What Is 1/2 + 1/4 As A Fraction
News Co
May 08, 2025 · 5 min read
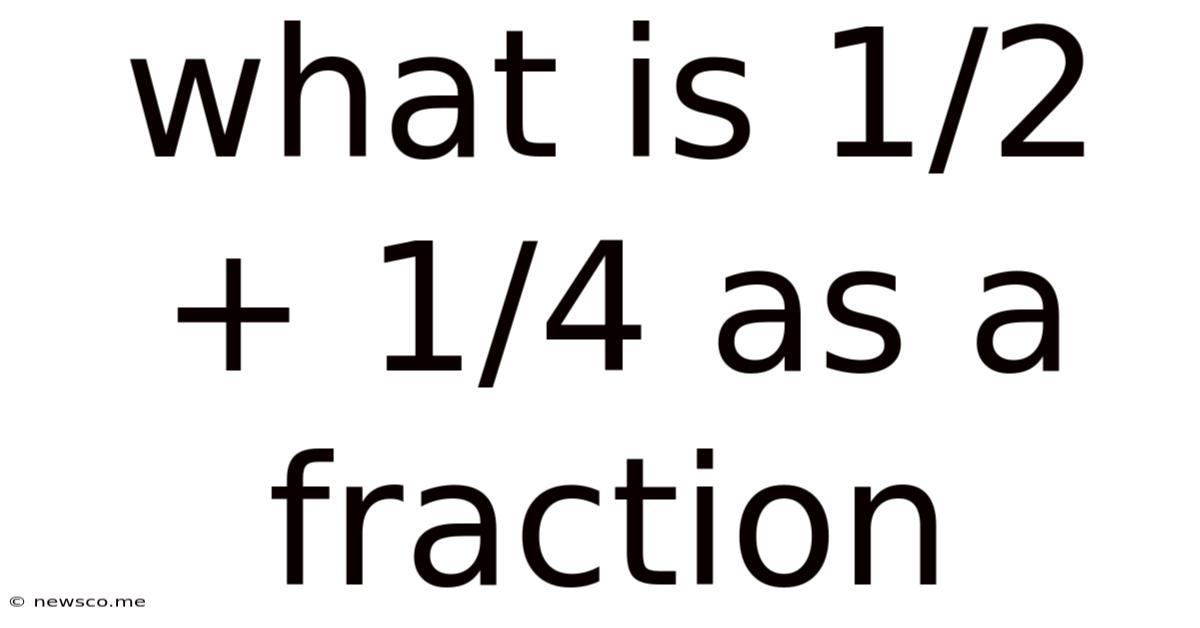
Table of Contents
What is 1/2 + 1/4 as a Fraction? A Comprehensive Guide to Fraction Addition
Adding fractions might seem daunting at first, but with a clear understanding of the underlying principles, it becomes a straightforward process. This comprehensive guide will walk you through adding 1/2 and 1/4, explaining the steps involved and providing valuable insights into fraction addition in general. We'll cover various methods, address common misconceptions, and equip you with the knowledge to tackle similar problems with confidence.
Understanding Fractions
Before diving into the addition, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number indicates how many parts you have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) signifies one part, and the denominator (2) signifies that the whole is divided into two equal parts.
Finding a Common Denominator
The crucial step in adding fractions is finding a common denominator. This is a number that is a multiple of both denominators. In our case, we need a common denominator for 2 and 4.
The easiest way to find a common denominator is to identify the least common multiple (LCM) of the denominators. The LCM of 2 and 4 is 4. This means we will convert both fractions so they have a denominator of 4.
Converting Fractions to a Common Denominator
To convert 1/2 to an equivalent fraction with a denominator of 4, we need to multiply both the numerator and the denominator by the same number. Since 2 multiplied by 2 equals 4, we multiply both the numerator and the denominator of 1/2 by 2:
(1 * 2) / (2 * 2) = 2/4
The fraction 1/4 already has the denominator of 4, so it doesn't need to be changed.
Adding the Fractions
Now that both fractions have a common denominator of 4, we can add them:
2/4 + 1/4 = (2 + 1) / 4 = 3/4
Therefore, 1/2 + 1/4 = 3/4
Visual Representation
Let's visualize this addition. Imagine a pizza cut into four slices. 1/2 of the pizza represents two of those slices (2/4). Adding another 1/4 slice gives you a total of three slices (3/4) out of the four total slices.
Different Methods for Finding the Common Denominator
While finding the LCM is the most efficient method, there are other ways to find a common denominator:
-
Listing multiples: Write down the multiples of each denominator until you find a common multiple. For 2 and 4:
- Multiples of 2: 2, 4, 6, 8...
- Multiples of 4: 4, 8, 12... The smallest common multiple is 4.
-
Multiplying the denominators: This method always works, but it doesn't always result in the least common denominator. Multiplying 2 and 4 gives 8. While this is a common denominator, it's larger than necessary and makes the simplification step more complex later.
Simplifying Fractions (Reducing to Lowest Terms)
After adding fractions, it's crucial to simplify the result, if possible, to express it in its lowest terms. A fraction is in its lowest terms when the greatest common divisor (GCD) of the numerator and denominator is 1.
In our case, 3/4 is already in its lowest terms because the GCD of 3 and 4 is 1.
Adding Fractions with Different Denominators: A Step-by-Step Guide
Let's generalize the process for adding any two fractions with different denominators:
-
Find the least common denominator (LCD): Determine the LCM of the two denominators.
-
Convert fractions to equivalent fractions: Convert each fraction to an equivalent fraction with the LCD as the denominator. Do this by multiplying both the numerator and denominator of each fraction by the appropriate factor.
-
Add the numerators: Add the numerators of the equivalent fractions. Keep the denominator the same.
-
Simplify (if necessary): Reduce the resulting fraction to its lowest terms by dividing both the numerator and denominator by their GCD.
Example: 2/3 + 1/5
Let's apply the steps to add 2/3 and 1/5:
-
LCD: The LCM of 3 and 5 is 15.
-
Convert:
- 2/3 = (2 * 5) / (3 * 5) = 10/15
- 1/5 = (1 * 3) / (5 * 3) = 3/15
-
Add: 10/15 + 3/15 = (10 + 3) / 15 = 13/15
-
Simplify: 13/15 is already in its lowest terms.
Common Mistakes to Avoid
-
Adding numerators and denominators directly: This is a common error. You must find a common denominator before adding the numerators.
-
Forgetting to simplify: Always check if the resulting fraction can be simplified to its lowest terms.
-
Incorrectly finding the LCD: Make sure you find the least common multiple, not just any common multiple.
Advanced Fraction Addition: More Than Two Fractions
The same principles apply when adding more than two fractions. Find the LCD for all denominators, convert all fractions to equivalent fractions with the LCD, add the numerators, and simplify the result.
Conclusion: Mastering Fraction Addition
Adding fractions, even those with different denominators, becomes manageable with a structured approach. Understanding the concept of a common denominator, mastering the steps involved, and avoiding common mistakes are key to achieving accuracy and confidence in your calculations. Remember to practice regularly to solidify your skills and tackle more complex fraction problems with ease. With consistent effort and practice, you'll master fraction addition and build a solid foundation in mathematics.
Latest Posts
Latest Posts
-
Square Root Of 81 Rational Or Irrational
May 08, 2025
-
Fifty Five Dollars On A Check
May 08, 2025
-
What Is The Fraction Of 9
May 08, 2025
-
Solving For Unknown Angles Worksheet Pdf
May 08, 2025
-
Difference Between T Test And F Test
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/2 + 1/4 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.