What Is 12 To The Power Of 2
News Co
May 08, 2025 · 5 min read
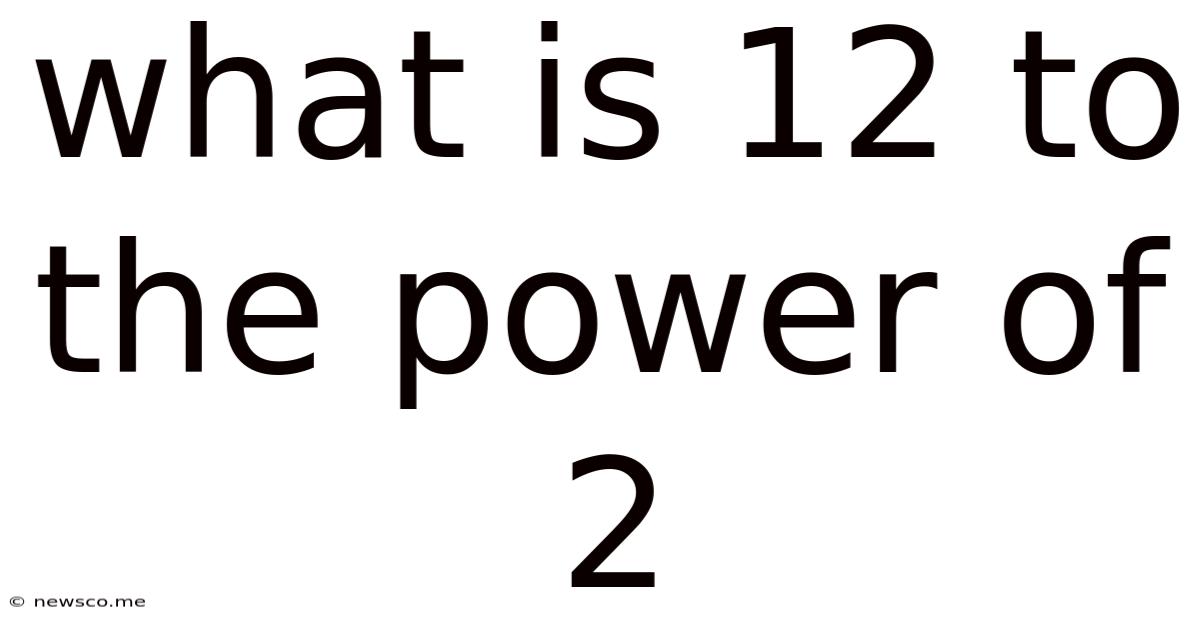
Table of Contents
What is 12 to the Power of 2? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 12 to the power of 2?" opens a door to a fascinating world of mathematics, specifically the concept of exponents. While the answer itself is straightforward (144), understanding the underlying principles and applications of exponents is crucial for various fields, from basic arithmetic to advanced calculus and computer science. This article will explore this seemingly simple equation in depth, examining its meaning, its calculations, and its broader implications.
Understanding Exponents: The Power of Repeated Multiplication
Before diving into the specifics of 12², let's establish a firm understanding of what exponents represent. An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression a<sup>b</sup>, 'a' is the base and 'b' is the exponent. This means 'a' is multiplied by itself 'b' times.
For example:
- 2³ = 2 x 2 x 2 = 8 (2 is multiplied by itself 3 times)
- 5² = 5 x 5 = 25 (5 is multiplied by itself 2 times)
- 10¹ = 10 (10 is multiplied by itself 1 time, or simply 10 itself)
- 7⁰ = 1 (Any non-zero number raised to the power of 0 equals 1)
This last example introduces another crucial concept: a number raised to the power of zero always equals 1 (except for 0⁰, which is undefined). This might seem counterintuitive, but it's a consistent rule within the mathematical system of exponents.
Calculating 12 to the Power of 2 (12²)
Now, let's return to our original question: What is 12 to the power of 2 (12²)? Following the definition of exponents, this means we need to multiply 12 by itself twice:
12² = 12 x 12 = 144
Therefore, 12 to the power of 2 is equal to 144. This is a fundamental calculation used in many areas.
Beyond the Basics: Properties of Exponents
The concept of exponents extends far beyond simple calculations like 12². Several key properties govern how exponents behave, allowing for more complex manipulations and simplifications:
1. Product of Powers:
When multiplying two numbers with the same base, you can add their exponents:
- a<sup>m</sup> x a<sup>n</sup> = a<sup>(m+n)</sup>
For example: 2³ x 2² = 2<sup>(3+2)</sup> = 2⁵ = 32
2. Quotient of Powers:
When dividing two numbers with the same base, you can subtract their exponents:
- a<sup>m</sup> / a<sup>n</sup> = a<sup>(m-n)</sup>
For example: 2⁵ / 2² = 2<sup>(5-2)</sup> = 2³ = 8
3. Power of a Power:
When raising a power to another power, you multiply the exponents:
- (a<sup>m</sup>)<sup>n</sup> = a<sup>(m x n)</sup>
For example: (2²)³ = 2<sup>(2 x 3)</sup> = 2⁶ = 64
4. Power of a Product:
When raising a product to a power, you raise each factor to that power:
- (ab)<sup>n</sup> = a<sup>n</sup>b<sup>n</sup>
For example: (2 x 3)² = 2² x 3² = 4 x 9 = 36
5. Power of a Quotient:
When raising a quotient to a power, you raise both the numerator and the denominator to that power:
- (a/b)<sup>n</sup> = a<sup>n</sup>/b<sup>n</sup>
For example: (2/3)² = 2²/3² = 4/9
Understanding these properties is crucial for efficiently solving more complex equations involving exponents.
Applications of Exponents: A Wide-Ranging Impact
The application of exponents extends far beyond the realm of pure mathematics. They are fundamental tools in numerous fields:
1. Science and Engineering:
Exponents are essential for representing scientific notations, particularly when dealing with extremely large or small numbers. For example, the speed of light is approximately 3 x 10⁸ meters per second. The exponent (8) allows for a concise representation of this massive number. They are also used extensively in physics, chemistry, and engineering formulas, including calculations involving exponential growth and decay.
2. Finance and Economics:
Compound interest calculations rely heavily on exponents. The formula for compound interest involves raising the principal amount to a power determined by the number of compounding periods. Understanding exponents is crucial for comprehending investment growth and loan repayment schedules.
3. Computer Science:
Binary numbers, the foundation of computer systems, utilize powers of 2. Each bit in a binary number represents a power of 2 (e.g., 2⁰, 2¹, 2², etc.). Exponents are also fundamental in algorithms and data structures, particularly those dealing with efficiency and scalability.
4. Statistics and Probability:
Exponents appear in various statistical formulas, including those related to probability distributions and hypothesis testing. Understanding exponents is crucial for analyzing data and drawing meaningful conclusions.
5. Geometry and Calculus:
Exponents are involved in numerous geometric calculations, such as finding the volume of spheres and cones. They also play a crucial role in calculus, especially in differentiation and integration, where exponential functions are frequently encountered.
Expanding on 12²: Further Explorations
While 12² = 144 provides a simple answer, let's delve deeper into its implications:
-
Factors of 144: Understanding the prime factorization of 144 (2⁴ x 3²) helps in simplifying expressions and solving equations involving 144.
-
Square Root of 144: The square root of 144 is 12, which is the inverse operation of squaring. This relationship between squaring and square rooting is fundamental in mathematics.
-
Geometric Representation: 144 can be visually represented as a square with sides of length 12 units. This connection between exponents and geometry provides a valuable visual interpretation of the concept.
-
Applications of 144: While seemingly an arbitrary number, 144 appears in various contexts, from the number of minutes in a day (1440) to certain geometric patterns and mathematical sequences.
Conclusion: The Enduring Significance of Exponents
The seemingly straightforward calculation of 12² reveals a much broader and more significant concept: exponents. Understanding exponents is not merely about performing calculations; it's about grasping a fundamental mathematical principle with far-reaching applications in numerous fields. From the simplicity of calculating 144 to the complexities of advanced scientific models, the power of exponents continues to shape our understanding of the world around us. This deep dive into 12² serves as a springboard for exploring the broader world of mathematics and its profound impact on our lives. The power of understanding is far greater than the power of simply knowing the answer.
Latest Posts
Latest Posts
-
How To Find Domain Of Composite Functions
May 09, 2025
-
Can Sample Variance Be Equal To Population Variance
May 09, 2025
-
Events That Cannot Occur At The Same Time Are Called
May 09, 2025
-
What Is 10 4 As A Decimal
May 09, 2025
-
What Does Area Under The Curve Mean In Statistics
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 12 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.